E1.3 Describe and perform translations and reflections on a grid, and predict the results of these transformations.
Skill: Describing and Performing Translations in a Grid
In Grade 4, students describe and perform vertical, horizontal, and diagonal translations. For example, to describe and perform a diagonal translation, both the horizontal and vertical movement must be considered. For example, a translation of three units to the right and two units down is symbolically represented as (3R, and 2D or (3→,and 2↓). The new image points are represented using the prime symbol (for example the original point A has the image point A’).
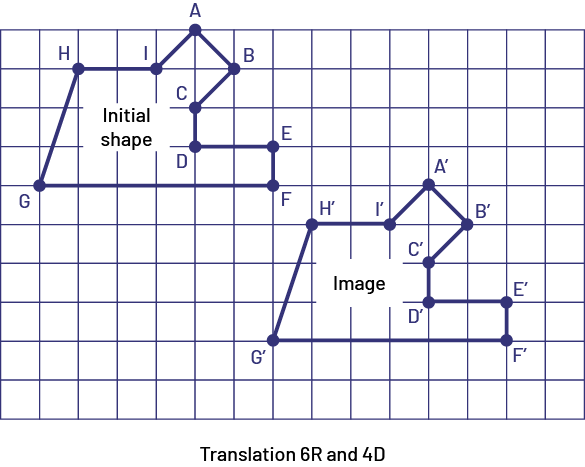image A grid of nine columns and 15 rows. There are two figures placed obliquely on the grid. In the first one is written initial figure; in the second one is written image. The points "a", "b", "c", "d", "e", "f", "g", "h", and "i" are identified on the initial figure. The points "a" apostrophe, "b" apostrophe, "c" apostrophe, "d" apostrophe, "e", "f" apostrophe, "g" apostrophe, "h" apostrophe, and "i" apostrophe are identified on the initial figure.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 2, p. 28-29.
Skill: Describing and Performing Reflections in a Grid
To describe and perform a reflection, it is necessary to understand that all points on the original shape and corresponding points on the image are equal distances from the line of reflection. The reflection causes a change in the original position and orientation of the shape but the reflected image is congruent with the original shape. In other words, the reflected image is the same size and shape, but it will be “oriented” in a different direction, and will be in a different position. It is important to note that the line of reflection can be drawn in any direction relative to the original shape-horizontally, vertically, or diagonally-at any angle; however, reflections from a diagonal line of reflection will be discussed in Grade 5.
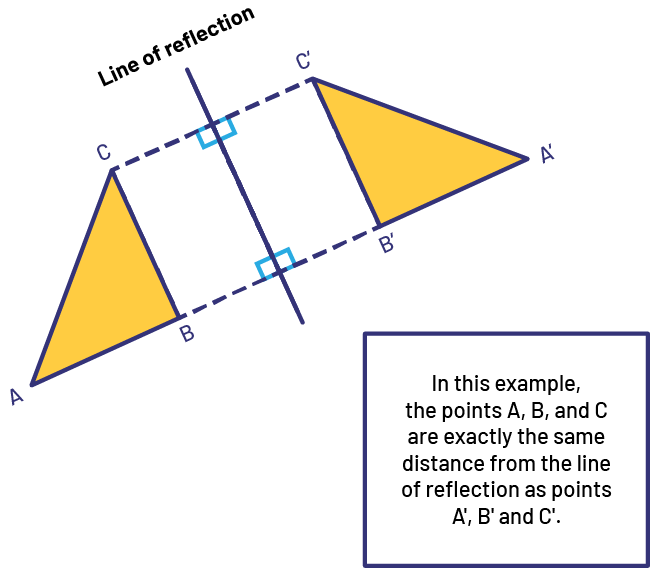image A quadrilateral formed by a rectangle and two congruent triangles of opposite sides. A line passes through the center of the figure. On one side, the points "a", "b", and "c" are identified; on the other side, the points "a" apostrophe, "b" apostrophe, and "c" apostrophe are identified.
Source: A Guide to effective Instruction in Mathematics, Grades 4- 6, p. 35.
Students should be able to perform reflections of simple and complex shapes on dot and grid paper, using the Mira and tracing paper or online dynamic geometry applications.
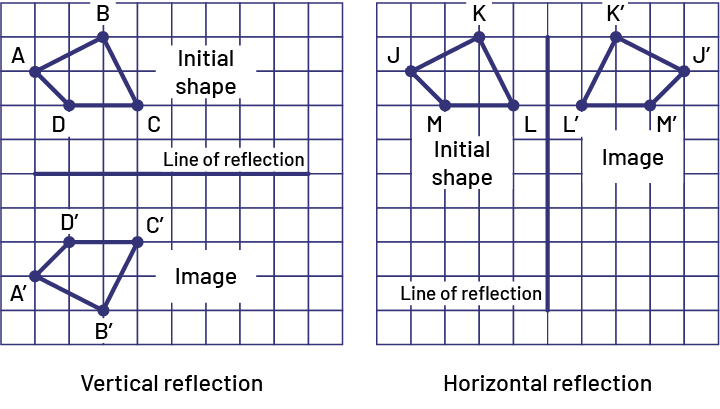image There are two grids: the first represents a vertical reflection, and the second represents a horizontal reflection. In the first grid, two congruent quadrilaterals are on either side of a horizontal line, called the reflection axis. The first quadrilateral is the initial figure; the second quadrilateral is the image. In the second grid, two congruent quadrilaterals are on one side each of a vertical line, named the reflection axis. The first quadrilateral is the initial figure; the second quadrilateral is the image.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 2, p. 31.
Skill: Predicting the Results of Translations and Reflections
In the junior grades, students predict the outcome of a translation and a reflection. Through guided investigations, students will eventually be able to visualize what the orientation and the location of the new image will be. Through guided investigations, students will eventually be able to observe the initial orientation of an object and the outcome of a transformation, and describe the transformation that has been completed without having to see it.
Source: A Guide to effective Instruction in Mathematics, Grades 4-6, p. 34.
Knowledge: Translation
A translation can be described as a transformation that slides each point of a shape the same distance and direction. During a translation, the orientation of the shape does not change and the image is congruent to the original shape. A translation can occur in any direction.
Source: A Guide to effective Instruction in Mathematics, Grades 4-6, p. 35.
Knowledge: Reflection
A reflection is a transformation in which all points on the initial shape and the corresponding points on the image are at equal distance from an axis of reflection.
Source: A Guide to effective Instruction in Mathematics, Grades 4-6, p. 35.