GEEM - Habiletés et connaissances

E2.1 Expliquer les relations entre des grammes et des kilogrammes comme unités de mesure métriques de la masse ainsi que des millilitres et des litres comme unités de mesure métriques de la capacité, et utiliser des repères représentant ces unités pour estimer la masse et la capacité.

HABILETÉ : EXPLIQUER DES RELATIONS ENTRE DES UNITÉS DE MESURE CONVENTIONNELLES

Relation inverse

Le nombre d’unités requis pour déterminer la mesure d’un attribut est inversement proportionnel à la grandeur de l’unité de mesure utilisée. Autrement dit :

plus l’unité de mesure utilisée est petite, plus le nombre d’unités requis pour déterminer la mesure de l’attribut est grand;
plus l’unité de mesure utilisée est grande, plus le nombre d’unités requis pour déterminer la mesure de l’attribut est petit.

Par exemple, si on mesure la durée d’une même activité une première fois en minutes et une deuxième fois en secondes, on aura un plus grand nombre de secondes que de minutes étant donné que la seconde est une unité de mesure plus petite que la minute. Quoique le concept de relation inverse puisse sembler évident dans ce genre de situation, il pose problème pour plusieurs élèves qui connaissent bien les situations de relation directe (par exemple, plus grande est la distance à parcourir en voiture, plus grande sera la durée du trajet). Afin de les aider à bien comprendre ce concept, le personnel enseignant doit leur présenter diverses situations concrètes de mesure qui les incitent à établir ce lien.

Exemple

Le personnel enseignant demande aux élèves de déterminer la capacité d’un contenant. Elle ou il remet un petit gobelet à la moitié des élèves et un gobelet plus grand à l’autre moitié. Pendant un échange mathématique, une partie des élèves indiquent, par exemple, que la capacité du contenant correspond à 10 gobelets alors que l’autre moitié indique qu’elle correspond à 30 gobelets. Le personnel enseignant incite ensuite les élèves à établir le lien entre la grandeur de l’unité de mesure utilisée et le nombre de ces unités requis pour établir la capacité du contenant en posant des questions telles que :

Pourquoi n’avez-vous pas toutes et tous obtenu la même mesure de capacité? (Parce que nous n’avons pas toutes et tous utilisé une unité de mesure de même grandeur.)
Quels sont ceux et celles qui ont utilisé le plus grand nombre d’unités de mesure? (Les élèves qui ont utilisé le plus petit gobelet comme unité de mesure.)
Quels sont ceux et celles qui ont utilisé le plus petit nombre d’unités de mesure? (Les élèves qui ont utilisé le plus grand gobelet comme unité de mesure.)
Pourquoi est-ce ainsi? (Parce qu’il faut remplir un plus grand nombre de fois le petit gobelet que le grand gobelet pour remplir le contenant.)

Afin d’inciter les élèves à pousser leur réflexion plus loin et à proposer une conjecture, le personnel enseignant leur présente ensuite un gobelet dont la grandeur se situe entre celle du petit gobelet et celle du grand gobelet, puis leur demande d’estimer la capacité du contenant en fonction de cette nouvelle unité de mesure et d’expliquer leur raisonnement.

« Je pense que la capacité du contenant correspond environ à 20 de ces gobelets parce que ce gobelet est plus petit que le plus grand gobelet. Il faudra donc utiliser plus de 10 fois cette mesure. Par contre, puisqu’il est plus grand que le plus petit gobelet, il faudra utiliser moins de 30 fois cette mesure. »

Enfin, le personnel enseignant incite les élèves à formuler une généralisation en posant des questions telles que :

Qu’advient-il du nombre d’unités utilisées lorsque la grandeur de l’unité de mesure augmente? Pourquoi? (Le nombre d’unités de mesure utilisées diminue. Il en faut moins parce que l’unité est plus grande.)
Qu’advient-il du nombre d’unités utilisées lorsque la grandeur de l’unité de mesure diminue? Pourquoi? (Le nombre d’unités de mesure utilisées augmente. Il en faut plus parce que l’unité est plus petite.)
Pouvez-vous expliquer en vos mots la relation qu’il y a entre la grandeur d’une unité de mesure et le nombre d’unités requis pour établir la mesure d’un attribut à l’aide de cette unité? (Plus l’unité utilisée pour déterminer la mesure de l’attribut est petite, plus le nombre d’unités requis est grand.)

Il importe que le personnel enseignant expose les élèves à ce genre de raisonnement dans diverses situations afin de les amener à bien comprendre la relation inverse et à reconnaître qu’elle s’applique à la mesure de n’importe quel attribut. Le personnel enseignant peut aussi profiter de diverses situations de mesure pour tester leur compréhension de cette relation en leur demandant de vérifier la vraisemblance de l’équivalence entre deux mesures quelconques.

Lorsque les élèves saisissent bien le concept de relation inverse entre le nombre d’unités requis pour déterminer une mesure et la grandeur de cette unité, elles et ils peuvent plus facilement comprendre et établir des relations entre certaines des unités de mesure conventionnelles.

Pour que les élèves puissent développer une bonne compréhension de ces relations, le personnel enseignant doit leur proposer des situations d’apprentissage qui leur permettent à la fois de donner un sens aux unités de mesure conventionnelles et d’explorer différentes stratégies de conversion d’une unité à l’autre. Ces stratégies reposent sur la reconnaissance que toute unité de mesure peut être exprimée :

en tant que multiple d’une unité de mesure plus petite (par exemple, un mètre équivaut à 1 000 millimètres, une minute équivaut à 60 secondes);
en tant que fraction d’une unité de mesure plus grande (par exemple, un mètre équivaut à \(\frac{1}{1000}\) de kilomètre, une minute équivaut à \(\frac{1}{60}\) d’une heure).

Source : Guide d’enseignement efficace des mathématiques de la 4^e à la 6^e année, p. 60-64.

HABILETÉ : ESTIMER DES MESURES

Au cycle moyen, les élèves doivent apprendre à utiliser diverses stratégies pour effectuer des estimations dans des situations de plus en plus complexes en utilisant à la fois des unités de mesure non conventionnelles et conventionnelles. Il importe donc que le personnel enseignant planifie des interventions et un enseignement formel axé sur des stratégies d’estimation particulières.

Van de Walle et Lovin (2008a, p. 296-297) proposent l’enseignement de quatre stratégies d’estimation. Ces stratégies sont présentées dans le tableau suivant.

Stratégie	Exemple
Développer et utiliser des repères qui représentent des unités de mesure importantes Les élèves qui se sont constitué un répertoire de repères et qui les utilisent régulièrement à estimer avec plus d'efficacité et d'aisance. L'estimation de la mesure de l'attribut se fait en le comparant à un repère.	Pour estimer la mesure d'un angle donné, les élèves peuvent utiliser l'angle droit et l'angle plat comme repères. En superposant mentalement l'image de ces angles sur l'angle donné, ils peuvent conclure que sa mesure est beaucoup plus près de 90^o que de 180^o. Ils estiment alors que la mesure de l'angle donné est d'environ 100^o. 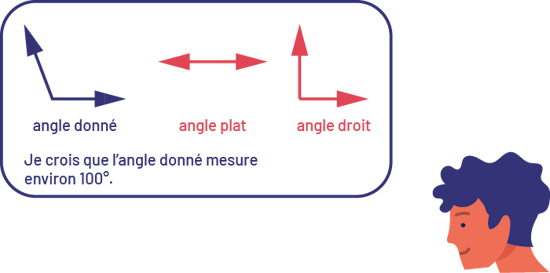image Dans un rectangle arrondi se trouvent trois angles: soit un angle donné qui est formé d’une courte ligne verticale et d’une courte ligne diagonale vers la gauche, un angle plat, et un angle droit. Au bas du rectangle est écrit: je crois que l’angle donné mesure environ cent degrés. À l’extérieur du rectangle, il y a un personnage.
Décomposer l'objet en parties Dans certains contextes, il est plus facile d'estimer la grandeur d'un objet en estimant d'abord la grandeur de plus petites sections facilement identifiables. L'estimation de la mesure de l'attribut correspond à la somme de la grandeur de chacune des sections.	Pour estimer la hauteur d'un édifice de 12 étages, les élèves peuvent d'abord estimer que la hauteur du premier étage est d'étage d'environ 3 m. En supposant que tous les étages ont la même hauteur, ils peuvent alors estimer que l'édifice mesure environ 36 m de haut.
Utilisation des subdivisions Si l’objet à mesurer ne comporte pas d’éléments qui suggèrent une façon de le décomposer en parties, on peut d’abord le diviser mentalement ou concrètement en demis. On peut ensuite diviser une de ces moitiés à nouveau en demis et répéter ainsi le processus jusqu’à l’obtention d’une section dont on peut estimer la mesure.	Pour estimer l’aire d’une grande couverture, les élèves peuvent la plier en deux à répétition jusqu’à ce qu’ils obtiennent une surface de couverture relativement petite. Il leur suffit alors d’estimer l’aire de cette surface, puis de multiplier le résultat par le nombre de ces surfaces ainsi créées. Note : Les élèves peuvent établir des liens avec le domaine Modélisation et algèbre et explorer la relation entre le nombre de plis et le nombre de surfaces créées en pliant, par exemple, une feuille de papier et en notant dans un tableau le nombre de surfaces identiques obtenues après chaque pli. Ils pourraient alors souligner que chaque fois qu’on ajoute un pli, le nombre de surfaces est doublé. 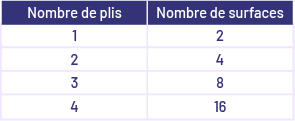image Un tableau à deux colonnes. La première colonne identifie le nombre de plis, alors que la deuxième représente le nombre de surfaces. Dans la première colonne sont les chiffres un, deux, trois, et quatre. Dans la deuxième colonne sont les chiffres deux, quatre, huit, et dix.
Faire des itérations mentalement et concrètement L’itération désigne l’acte de placer, à plusieurs reprises et d’une manière ordonnée, une même unité de mesure de façon à déterminer la mesure d’un attribut quelconque. L’estimation de la mesure de l’attribut correspond au nombre de fois que l’unité est placée.	Pour estimer l’aire d’un carton en utilisant un papillon autocollant comme unité de mesure, les élèves peuvent tenter de visualiser le nombre de fois qu’un papillon peut être placé sur le carton sans faire de chevauchements ni laisser d’espaces.

Lorsque les élèves effectuent des activités d’estimation de façon régulière, elles et ils se rendent compte qu’il n’y a pas qu’une seule stratégie efficace d’estimation. Le personnel enseignant doit donc leur proposer de fréquentes activités d’estimation ayant trait aux attributs mesurables. Ces activités s’avèrent pertinentes si les élèves discutent, justifient et expliquent la façon de parvenir à leurs résultats. Les explications et justifications des estimations faites par les élèves permettent au personnel enseignant de connaître et même d’évaluer leur compréhension des concepts et des procédures en mesure.

Source : Guide d’enseignement efficace des mathématiques de la 4^e à la 6^e année, p. 18-20.

HABILETÉ : UTILISER DES REPÈRES ASSOCIÉS À L’ATTRIBUT DE LA MASSE

Selon Lindsay et Scott (2005, p. 3), il est très difficile de concevoir des repères pour l’attribut masse en raison de la différence entre l’acuité visuelle et l’acuité tactile. En effet, la vue permet généralement de reconnaître de très petites différences de longueur entre deux objets. Par contre, il est plutôt difficile, en soupesant deux objets, de discerner une petite différence de masse (par exemple, différence de moins de 100 g). Le personnel enseignant doit fournir aux élèves de multiples occasions de soupeser divers objets pour les aider à concevoir des repères de masse (par exemple, un sac de sucre a une masse de 2 kg ou de 2 000 g).

Soulignons que le volume d’un objet influe parfois sur la perception que l’on peut avoir de sa masse. Ainsi, les élèves ont parfois l’impression qu’un objet de grand volume a nécessairement une plus grande masse qu’un objet de petit volume. De même, lorsque les élèves observent deux objets de même volume, certains ont l’impression qu’ils ont nécessairement la même masse. Il leur suffit de penser à deux boîtes de mêmes dimensions, l’une remplie de livres et l’autre remplie d’oreillers de plumes, pour comprendre qu’il n’en est rien.

Source : Guide d’enseignement efficace des mathématiques de la 4^e à la 6^e année, p. 15.

HABILETÉ : UTILISER DES REPÈRES ASSOCIÉS À L’ATTRIBUT DE LA CAPACITÉ

La capacité fait référence à la quantité d’une substance qu’un emballage peut contenir. Il est parfois difficile pour les élèves de concevoir des repères pour cet attribut, puisque la capacité d’un emballage peut s’exprimer en grammes (par exemple, capacité d’une boîte de céréales), en millilitres ou en litres (par exemple, capacité d’un contenant de jus) ou encore en centimètres cubes (par exemple, capacité d’une boîte d’emballage). Elle peut aussi s’exprimer en fonction du nombre d’objets identiques qu’un emballage peut contenir (par exemple, un contenant cylindrique qui a une capacité de trois balles de tennis). Soulignons aussi que, puisque les liquides prennent la forme du contenant dans lequel ils sont versés, il est difficile de se faire une image mentale d’une capacité de 1 l ou de 1 ml sans tenir compte du contenant. Le personnel enseignant peut inciter les élèves à utiliser divers articles que l’on trouve à la maison afin de concevoir des repères pour l’attribut capacité (par exemple, sac de 1 l de lait, bouteille d’eau de 500 ml, boîte de 250 g de biscuits).

Source : Guide d’enseignement efficace des mathématiques de la 4^e à la 6^e année, p. 16.

CONNAISSANCE : RELATIONS ENTRE DES UNITÉS DE MESURE MÉTRIQUES DE LA MASSE (GRAMMES ET KILOGRAMMES)

Le gramme et le kilogramme sont des unités de masse du système métrique.

Un kilogramme (kg) équivaut à 1 000 grammes (g).
Un millilitre (1 ml) d’eau a une masse d’un gramme (1 g).

Source: Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1^re à la 8^e année, 2020, Ministère de l’Éducation de l’Ontario.

On utilise le fait que les diverses unités de mesure conventionnelles associées à l’attribut masse font partie d’un système décimal d’unités pour établir des relations d’équivalence entre ces unités.

Exemple 1

Puisque le gramme (g) est 1 000 fois plus petit que le kilogramme (kg), on peut établir la relation d’équivalence suivante :

1 000 g = 1 kg

Les élèves ont besoin d’explorer plusieurs situations d’apprentissage avec du matériel concret pour développer une bonne compréhension de ces relations d’équivalence. Afin de pouvoir passer aisément d’une unité de mesure à l’autre, les élèves doivent aussi bien comprendre le concept de relation inverse.

Au fur et à mesure que les élèves explorent de telles situations d’apprentissage, le personnel enseignant les incite à mettre en pratique leur compréhension des relations entre les unités de mesure utilisées pour proposer une conjecture, puis formuler une généralisation.

Exemple 2

Après avoir découvert qu’un kilomètre équivaut à 1 000 mètres (1 km = 1 000 m), les élèves peuvent proposer la conjecture suivante : un kilogramme équivaut à 1 000 grammes (1 kg = 1 000 g). Les élèves peuvent ensuite vérifier cette conjecture, puis formuler une généralisation, soit que le préfixe kilo- placé devant une unité de mesure désigne une mesure équivalant à mille fois cette unité.

Source : Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, p. 64-66.

CONNAISSANCE : RELATIONS ENTRE DES UNITÉS DE MESURE MÉTRIQUES DE LA CAPACITÉ (MILLILITRES ET LITRES)

Le millilitre et le litre sont des unités de capacité conventionnelles du système métrique.

Un litre (l) équivaut à 1 000 millilitres (ml).
Un millilitre (1 ml) d’eau a une masse d’un gramme (1 g).
Un millilitre (1 ml) de liquide occupe l’espace d’un cube de 1 cm sur 1 cm sur 1 cm, soit d’un centimètre cube (1 cm³).

Source: Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1^re à la 8^e année, 2020, Ministère de l’Éducation de l’Ontario.

On utilise le fait que les diverses unités de mesure conventionnelles associées à l’attribut capacité font partie d’un système décimal d’unités pour établir des relations d’équivalence entre ces unités.

Exemple 1

Puisque le millilitre (ml) est 1 000 fois plus petit que le litre (l), on peut établir la relation d’équivalence suivante :

1 000 ml = 1 l.

Exemple 2

Le personnel enseignant demande aux élèves de verser un litre d’eau dans une éprouvette graduée, puis leur demande de noter le volume d’eau dans l’éprouvette en millilitres. Il fait ressortir l’équivalence suivante : 1 l = 1 000 ml.

Le personnel enseignant incite ensuite les élèves à mettre en pratique leur compréhension de la relation inverse pour établir des relations entre les unités de mesure utilisées en posant des questions telles que :

Pourquoi le nombre correspondant à la mesure du volume d’eau dans l’éprouvette est-il plus petit lorsque le volume est exprimé en litres que lorsqu’il est exprimé en millilitres? (L’unité de mesure litre est plus grande que l’unité de mesure millilitre. Il faut donc moins de litres que de millilitres pour représenter le même volume d’eau.)
Combien de fois moins de litres que de millilitres d’eau y a-t-il dans l’éprouvette? (On a noté que le volume d’eau dans l’éprouvette correspondait à 1 000 ml. Il y a donc 1 000 fois moins de litres que de millilitres d’eau dans l’éprouvette.)
L’unité de mesure litre est-elle beaucoup plus grande que l’unité de mesure millilitre? Comment le savez-vous? (Puisque le nombre de millilitres d’eau dans l’éprouvette est 1 000 fois plus petit que le nombre de litres, on peut conclure que l’unité de mesure litre est 1 000 fois plus grande que l’unité de mesure millilitre.)
Comment pouvez-vous décrire symboliquement la relation entre les litres et les millilitres? (1 l = 1 000 ml)

Exemple 3

Après avoir découvert qu’un millimètre équivaut à un millième de 1 mètre (1 mm = 0,001 m), les élèves peuvent proposer la conjecture suivante : un millilitre équivaut à un millième de 1 litre (1 ml = 0,001 l). Les élèves peuvent ensuite vérifier cette conjecture, puis formuler une généralisation, soit que le préfixe milli- placé devant une unité de mesure désigne une mesure équivalant à un millième de cette unité. Ainsi, un milligramme équivaut à un millième d’un gramme (1 mg = 0,001 g).

Source : Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, p. 64-66.