E2.1 Explain the relationships between grams and kilograms as metric units of mass, and between litres and millilitres as metric units of capacity, and use benchmarks for these units to estimate mass and capacity.
Skill: Explaining Relationships Between Standard Units
Inverse Relationship
The number of units required to determine the measurement of an attribute is inversely proportional to the size of the unit used. In other words:
- the smaller the unit used, the greater the number of units required to determine the measurement of the attribute;
- the larger the unit used, the smaller the number of units required to determine the measurement of the attribute.
For example, if the duration of the same activity is measured once in minutes and a second time in seconds, there will be more seconds than minutes because the second is a smaller unit than the minute. Although the concept of an inverse relationship may seem obvious in this type of situation, it is problematic for many students who are familiar with direct relationship situations (for example, the greater the distance to be travelled by car, the greater the duration of the trip). In order to help them understand this concept, teachers should present them with a variety of concrete measurement situations that encourage them to make this connection.
Example
The teacher asks students to determine the capacity of a container. They give half of the students a small cup and the other half a larger cup. During a math conversation, some of the students indicate, for example, that the capacity of the container is 10 cups while the others indicate that it is 30 cups. The teacher then prompts students to relate the size of the unit used and the number of such units required to determine the capacity of the container by asking questions such as:
- Why didn't you all get the same measurement of capacity? (Because we didn't all use the same size unit.)
- Which students had the largest number of units? (Students who used the smaller cup as a unit.)
- Which students had the smallest number of units? (The students who used the larger cup as a unit.)
- Why is this? (Because you have to fill the small cup more times than the large cup to fill the container.)
To encourage students to think further and propose a conjecture, the teacher then presents them with a cup that is between the size of the small cup and the large cup, and asks them to estimate the capacity of the container in terms of this new unit and explain their reasoning.
“I think the capacity of the container is about 20 of these cups because this cup is smaller than the largest cup, so we will need more than 10 of them. On the other hand, since it is larger than the smallest cup, we will need to use less than 30 of them.”
Finally, the teacher encourages students to formulate a generalization by asking questions such as:
- What happens to the number of units used when the size of the unit increases? Why? (The number of units used decreases. Fewer units are needed because the unit is larger.)
- What happens to the number of units used when the size of the unit decreases? Why? (The number of units used increases. More units are needed because the unit is smaller.)
- Can you explain in your own words the relationship between the size of a unit and the number of units required to establish the measurement of an attribute using that unit? (The smaller the unit used to determine the measurement of the attribute, the greater the number of units required.)
It is important for teachers to expose students to this type of reasoning in a variety of situations to ensure that they understand the inverse relationship and recognize that it applies to the measurement of any attribute. Teachers can also use a variety of measurement situations to test students' understanding of this inverse relationship by asking them to test the reasonableness of the equivalence of any two measurements.
When students have a good grasp of the concept of an inverse relationship between the number of units required to determine a measurement and the size of that unit, they can more easily understand and establish relationships between some of the standard units.
In order for students to develop an understanding of these relationships, teachers should provide learning experiences that allow them to both make sense of standard units and explore different strategies for converting from one unit to another. These strategies are based on the recognition that any unit can be expressed:
- as a multiple of a smaller unit (for example, one metre equals 1000 millimetres);
- as a fraction of a larger unit (for example, one metre is \(\frac{1}{1000}\) of a kilometre).
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Mesure, p. 60-64.
Skill: Estimating Measurements
In the primary grades, students must learn to use a variety of strategies to make estimates in increasingly complex situations using both non-standard and standard units, so it is important that teachers plan learning experiences and formal instruction focused on specific estimation strategies.
Van de Walle and Lovin (2008) suggest teaching four estimation strategies. These strategies are shown in the following table.
|
Strategy |
Example |
|
Develop and Use Benchmarks That Represent Important Units of Measurement Students who have built up a repertoire of reference points or benchmarks and use them regularly are more successful and comfortable estimating. Estimating the measurement of the attribute is done by comparing it with a benchmark. |
To estimate the measurement of a given angle, students can use the right angle and the flat angle as benchmarks. By mentally superimposing the image of these angles on the given angle, they can conclude that its measure is much closer to 90° than 180°. They then estimate that the measurement of the given angle is about 100°. 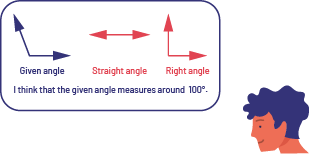 image In a rounded rectangle, there are three angles: a given angle which is formed by a short vertical line and a short diagonal line to the left, a flat angle, and a right angle. At the bottom of the rectangle is written: I believe that the given angle measures about one hundred degrees. Outside the rectangle, there is a character. |
|
Break Down the Object into Parts In some contexts, it is easier to estimate the measure of an attribute for an object by first estimating the size of smaller, easily identifiable parts of that object. The estimate will be the sum of the size of each of the parts. |
Students can first estimate that the height of the first floor is about 3 m. Assuming that all floors are the same height, they can then estimate that the building is about 36 m high.  |
|
Use of Subdivisions If the object to be measured has no elements that suggest a way to break it down into parts, it can first be divided mentally or concretely into halves, and then one of these halves can be divided again into halves and the process repeated until a section is obtained whose measurement can be estimated. |
To estimate the area of a large blanket, students can fold it in half repeatedly to create a relatively small blanket surface. They can then estimate the area of this surface and multiply the result by the number of such surfaces created.  Note: Students can make connections to the Algebra strand and explore the relationship between the number of folds and the number of surfaces created by, for example, folding a piece of paper and recording in a chart the number of identical surfaces obtained after each fold. They could then point out that each time a fold is added, the number of surfaces is doubled. 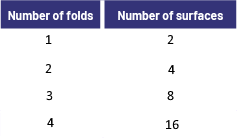 image A table with two columns. The first column identifies the number of folds, while the second column represents the number of surfaces. In the first column are the numbers one, two, three, and four. In the second column are the numbers two, four, eight, and ten. |
|
Iterate Concretely or Mentally Iteration refers to the act of placing, repeatedly and in an orderly fashion, the same unit in order to determine the measurement of an attribute. The number of times the unit is placed then corresponds to the measurement of the attribute. |
To estimate the area of a box using a sticky note as a unit, students can try to visualize how many times a sticky note can be placed on the box without overlapping or leaving gaps.  |
When students engage in estimation activities on a regular basis, they realize that there is no single effective estimation strategy. Teachers should provide students with frequent estimation activities related to measurable attributes. These activities are most effective when students discuss, justify, and explain how they arrived at their results. Explanations and justifications of students' estimates allow teachers to learn about, and even assess, their understanding of measurement concepts and procedures.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Mesure, p. 18-20.
Skill: Using Benchmarks Associated with Mass
According to Lindsay and Scott (2005), it is very difficult to select benchmarks for mass because of the difference between visual acuity and tactile acuity. Indeed, sight generally makes it possible to identify very small differences in length between two objects. On the other hand, it is rather difficult, by weighing two objects, to discern a small difference in mass (for example, difference of less than 100 grams) benchmarks (for example, a paperclip has a mass of 1 gram, 4 bananas have a mass of approximately 500 grams).
Note that the volume of an object sometimes affects the perception of its mass. For example, students may have the impression that a larger object must have a greater mass than a smaller object. Similarly, when students look at two objects of the same volume, some have the impression that they necessarily have the same mass. They just have to think of two boxes of the same dimensions, one filled with books and the other filled with feather pillows, to realize that this is not the case.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Mesure, p. 15.
Skill: Using Benchmarks Associated with Capacity
Capacity refers to the amount of a substance that a package can hold. It is sometimes difficult for students to decide on benchmarks for this attribute, since the capacity of a package can be expressed in grams (for example, the capacity of a cereal box), in millilitres or in litres (for example, the capacity of a juice container) or in cubic centimetres (for example, the capacity of a packaging box). Capacity can also be expressed as the number (count) of identical objects that a package can contain (for example, a cylindrical container that has a capacity of three tennis balls). It should also be noted that, since liquids take the shape of the container in which they are poured, it is difficult to form a mental image of a capacity of 1 L or 1 mL without taking the container into account. Teachers can encourage students to use various items found around the house to use as benchmarks for capacity (for example, a 1 L bag of milk, a 500 mL bottle of water, a 250 g box of cookies).
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Mesure, p. 16.
Knowledge: Relationships Between Metric Units of Mass (Grams and Kilograms)
The gram and the kilogram are units of mass in the metric system.
- One kilogram (kg) is equivalent to 1000 grams (g).
- One millilitre (1 mL) of water has a mass of one gram (1 g).
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
The fact that the various standard units associated with mass are part of a decimal system of units is used to establish equivalence relationships between these units.
Example 1
Since the gram (g) is 1000 times smaller than the kilogram (kg), the following equivalence relationship can be established:
1000 g = 1 kg
Students should explore several learning experiences with concrete materials to develop a good understanding of these equivalence relationships. In order to be able to move easily from one unit to another, students also need to have a good understanding of the concept of inverse relationships.
As students explore such learning situations, teachers should encourage them to propose a conjecture about the relationship between the units, test it, and then formulate a generalization.
Example 2
With the understanding that one kilometre equals 1000 metres (1 km = 1000 m), ask students to make a conjecture about how many grams are in1 kilogram. Ask students to verify this conjectures, and support them in formulating a generalization, namely that the prefix kilo- placed in front of a unit designates a measurement equivalent to one thousand times that unit.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Mesure, p. 64-66.
Knowledge: Relationships Between Metric Units of Capacity (Millilitres and Litres)
The millilitre and the litre are conventional units of capacity in the metric system.
- One liter (L) is equivalent to 1000 millilitres (mL).
- One millilitre (1 mL) of water has a mass of one gram (1 g).
- One millilitre (1 mL) of liquid occupies the space of a 1 cm by 1 cm by 1 cm cube, or one cubic centimetre (1 cm3).
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
The fact that the various standard units associated with capacity are part of a decimal system of units is used to establish equivalence relationships between these units.
Example 1
Since the millilitre (mL) is 1000 times smaller than the litre (L), we can establish the following equivalence relationship:
1000 mL = 1 L
Students should explore several learning experiences with concrete materials to develop a good understanding of these equivalence relationships. In order to be able to move easily from one unit to another, students also need to have a good understanding of the concept of inverse relationships.
Example 2
Ask students to pour one litre of water into a graduated cylinder and then asks them to record the volume of water in the cylinder in millilitres. Point out the following equivalence: 1 L = 1000 mL.
Ask students to apply their understanding of the inverse relationship to establish relationships between the units used by asking questions such as:
- Why is the number corresponding to the measurement of the volume of water in the graduated cylinder smaller when the volume is expressed in litres than when it is expressed in millilitres? (The litre is larger than the millilitre, so fewer litres than millilitres are needed to represent the same volume of water.)
- How many times fewer litres than millilitres of water are there in the graduated cylinder? (The volume of water in the graduated cylinder was recorded as 1000 mL, so there are 1000 times fewer litres than millilitres of water in the graduated cylinder.)
- Is the litre much larger than the millilitre? How do you know? (Since the number of millilitres of water in the graduated cylinder is 1000 times smaller than the number of litres, we can conclude that the litre is 1000 times larger than the millilitre.)
- How can you symbolically describe the relationship between litres and millilitres? (1 L = 1000 mL)
As students explore such learning situations, teachers should encourage them to apply their understanding of the relationships among the units used to propose a conjecture and then formulate a generalization.
Example 3
With the understanding that one millimetre is one thousandth of a metre (1 mm = 0.001 m), ask students to make a conjecture about how many litres are in one millilitre (one millilitre is one thousandth of a litre or 1 mL = 0.001 L). Ask students to verify their conjecture and then lead support them in making a generalization that the prefix milli- in front of a unit refers to a measurement that is one thousandth of that unit. For example, one milligram is one thousandth of a gram (1 mg = 0.001 g).
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Mesure, p. 64-66.