E2.2 Utiliser des préfixes métriques pour décrire la taille relative de différentes unités de mesure métriques et choisir l’unité et l’instrument de mesure appropriés pour mesurer la longueur, la masse et la capacité.
HABILETÉ : UTILISER DES PRÉFIXES MÉTRIQUES POUR DÉCRIRE LA TAILLE RELATIVE DE DIFFÉRENTES UNITÉS DE MESURE MÉTRIQUES
Lorsque les élèves saisissent bien le concept de relation inverse entre le nombre d’unités requis pour déterminer une mesure et la grandeur de cette unité, elles et ils peuvent plus facilement comprendre et établir des relations entre certaines des unités de mesure conventionnelles.
Pour que les élèves puissent développer une bonne compréhension de ces relations, le personnel enseignant doit leur proposer des situations d’apprentissage qui leur permettent à la fois de donner un sens aux unités de mesure conventionnelles et d’explorer différentes stratégies de conversion d’une unité à l’autre. Ces stratégies reposent sur la reconnaissance que toute unité de mesure peut être exprimée :
- en tant que multiple d’une unité de mesure plus petite (par exemple, un mètre équivaut à 1 0 millimètres, une minute équivaut à 60 secondes);
- en tant que fraction d’une unité de mesure plus grande (par exemple, un mètre équivaut à \(\frac{1}{1000}\) de kilomètre, une minute équivaut à \(\frac{1}{60}\) d’une heure).
Relations entre des unités de mesure des attributs longueur, masse et capacité
On utilise le fait que les diverses unités de mesure conventionnelles associées aux attributs longueur, masse et capacité font partie d’un système décimal d’unités pour établir des relations d’équivalence entre ces unités. Par exemple, puisque le gramme (g) est 10 fois plus grand que le décigramme (dg) et 10 fois plus petit que le décagramme (dag), on peut établir les relations d’équivalence suivantes : 1 g = 10 dg, 1 g = 0,1 dag. Les élèves ont besoin d’explorer plusieurs situations d’apprentissage avec du matériel concret pour développer une bonne compréhension de ces relations d’équivalence. Afin de pouvoir passer aisément d’une unité de mesure à l’autre, les élèves doivent aussi bien comprendre le concept de relation inverse.
Exemple 1
Le personnel enseignant remet un mètre à chaque équipe et demande aux élèves d’en couvrir un dixième avec un carton. Il pose ensuite les questions suivantes :
- Que représente un dixième d’un mètre? (1 dm, 10 cm ou 100 mm)
- Quelles relations peut-on alors établir entre le décimètre, le centimètre et le millimètre? (1 dm = 10 cm, 1 dm = 100 mm, 10 cm = 100 mm)
Note : Le raisonnement qui permet d’établir ces relations est fondé sur le concept de transitivité. Il peut ensuite inciter les élèves à découvrir d’autres relations entre les unités de mesure de longueur en leur demandant de couvrir un dixième d’un décimètre, un dixième d’un centimètre, un centième d’un mètre ou encore un centième d’un décimètre.
Exemple 2
Le personnel enseignant demande aux élèves de verser un litre d’eau dans une éprouvette graduée, puis leur demande de noter le volume d’eau dans l’éprouvette en centilitres et en millilitres. Il fait ressortir les équivalences suivantes : 1 l = 100 cl, 1 l = 1 000 ml. Il incite ensuite les élèves à mettre en pratique leur compréhension de la relation inverse pour établir des relations entre les unités de mesure utilisées en posant des questions telles que :
- Pourquoi le nombre correspondant à la mesure du volume d’eau dans l’éprouvette est-il plus petit lorsque le volume est exprimé en centilitres que lorsqu’il est exprimé en millilitres? (L’unité de mesure centilitre est plus grande que l’unité de mesure millilitre. Il faut donc moins de centilitres que de millilitres pour représenter le même volume d’eau.)
- Combien de fois moins de centilitres que de millilitres d’eau y a-t-il dans l’éprouvette? (On a noté que le volume d’eau dans l’éprouvette correspondait à 1 000 ml ou à 100 cl. Il y a donc 10 fois moins de centilitres que de millilitres d’eau dans l’éprouvette.)
- L’unité de mesure centilitre est-elle beaucoup plus grande que l’unité de mesure millilitre? Comment le savez-vous? (Puisque le nombre de centilitres d’eau dans l’éprouvette est 10 fois plus petit que le nombre de millilitres, on peut conclure que l’unité de mesure centilitre est 10 fois plus grande que l’unité de mesure millilitre.)
- Comment pouvez-vous décrire symboliquement la relation entre les centilitres et les millilitres? (1 cl = 10 ml)
Le personnel enseignant peut ensuite inciter les élèves à démontrer leur compréhension des relations entre les unités de mesure en appliquant le même type de raisonnement à une autre situation. Par exemple, il leur indique que le décilitre est une unité de mesure 10 fois plus grande que le centilitre, puis leur demande :
- Selon vous, combien de décilitres d’eau y a-t-il dans l’éprouvette? Pourquoi? (On sait qu’il y a 100 cl d’eau dans l’éprouvette. Puisque l’unité de mesure décilitre est 10 fois plus grande que l’unité de mesure centilitres, le nombre de décilitres d’eau dans l’éprouvette doit être 10 fois plus petit que 100. Il doit donc y avoir 10 dl d’eau dans l’éprouvette.)
Au fur et à mesure que les élèves explorent de telles situations d’apprentissage, le personnel enseignant les incite à mettre en pratique leur compréhension des relations entre les unités de mesure utilisées pour proposer une conjecture, puis formuler une généralisation. Par exemple, après avoir découvert qu’un millimètre équivaut à un millième d’un mètre (1 mm = 0,001 m), les élèves peuvent proposer la conjecture suivante : un millilitre équivaut à un millième d’un litre (1 ml = 0,001 l). Les élèves peuvent ensuite vérifier cette conjecture, puis formuler une généralisation, soit que le préfixe milli- placé devant une unité de mesure désigne une mesure équivalant à un millième de cette unité. Ainsi, un milligramme équivaut à un millième d’un gramme (1 mg = 0,001 g).
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 64-66.
HABILETÉ : CHOISIR L’UNITÉ ET L’INSTRUMENT DE MESURE APPROPRIÉS
L’acte de mesurer consiste à choisir une unité de mesure non conventionnelle ou conventionnelle appropriée pour mesurer un attribut quelconque d’un objet. Pour ce faire, il importe de choisir une unité qui reflète l’attribut à mesurer et qui se prête bien à la situation. De plus, il est généralement préférable d’utiliser une seule et même unité de mesure. Enfin, il importe aussi que le choix de l’unité tienne compte du degré de précision de la mesure recherché (par exemple, une mesure de masse au kilogramme ou au gramme près).
Au moment des premières explorations d’un attribut d’un objet, il est préférable que le personnel enseignant incite
d’abord les élèves à choisir une unité de mesure non conventionnelle, et ce, afin de leur permettre de mieux
comprendre le sens de l’attribut et de sa mesure. Par la suite, il peut faire ressortir les limites de l’unité
choisie et les avantages d’utiliser une unité de mesure
conventionnelle.
Exemple
Le personnel enseignant de 4e année propose aux élèves de déterminer l’aire d’un tapis d’exercice. Il leur présente divers objets (par exemple, jeton circulaire, carreau algébrique, papillon adhésif, boîtier de téléphone intelligent, grand carton, ballon) et leur demande d’indiquer, pour chacun, si l’objet constitue un bon choix d’unité de mesure pour cette tâche et d’expliquer leur réponse. Le tableau ci-dessous présente des exemples de réponse possible.
|
Objet |
Réponse possible |
|
Jeton circulaire |
Ce n'est pas un bon choix parce que sa forme circulaire ne se prête pas bien à la mesure de l'aide d'une surface rectangulaire. |
|
Carreau algébrique Papier autocollant |
La forme rectangulaire de ces deux objets reflète bien l'attribut à mesurer. Par contre, puisqu’il faudrait un très grand nombre de chacun de ces objets pour recouvrir le tapis, ils ne constituent pas les meilleurs choix comme objet étalon. |
|
Boîtier de téléphone intelligent Grand carton |
Chacun de ces objets constituent un bon choix d'objet étalon parce qu'il est facile de les utiliser pour recouvrir le tapis et ainsi déterminer son aire. Il importe de souligner que dans le cas de boîtier de téléphone intelligent, c'est l'aire d'une des faces qui sert d'unité de mesure. |
|
Ballon |
Ce n'est pas un bon choix parce que sa surface courbe ne se prête pas à la mesure de l'aire du tapis. |
Afin de s’assurer que les élèves comprennent bien le sens d’une unité de mesure, le personnel enseignant demande à
quelques élèves de montrer comment le boîtier de téléphone intelligent et les grands cartons pourraient être
utilisés pour déterminer l’aire du tapis. Les élèves montrent alors la façon dont il est possible de recouvrir le
tapis à l’aide de chacun de ces objets.
Le personnel enseignant incite ensuite les élèves à
réfléchir aux désavantages d’utiliser ces unités de mesure pour déterminer l’aire du tapis en posant des questions
telles que :
- Si je vous disais que l’aire du tapis est égale à l’aire de six grands cartons, auriez-vous une bonne image de l’aire du tapis? Justifiez votre réponse. (Oui, mais seulement dans la mesure où on a une bonne image mentale du carton utilisé. Sinon, il n’est pas possible de se faire une bonne image de l’aire du tapis.)
- Au moment d’acheter du tissu pour recouvrir le tapis, serait-il utile de dire à la vendeuse ou au vendeur que l’aire du tapis correspond à l’aire de 36 faces d’un boîtier de téléphone intelligent? Pourquoi? (Non, parce que ce n’est pas une unité de mesure qui est couramment utilisée pour décrire une quantité de tissu.)
En reprenant l’activité à l’aide de centimètres carrés ou de mètres carrés comme unités de mesure, le personnel enseignant peut souligner que ces unités sont dites conventionnelles parce qu’elles sont employées couramment par un grand nombre de personnes et qu’elles ont, par le fait même, l’avantage de rendre la communication de la mesure claire. Il peut aussi faire ressortir le fait que les unités de mesure conventionnelles choisies doivent aussi refléter l’attribut à mesurer, se prêter à la situation et être de préférence identiques afin d’être utiles et appropriées pour résoudre la situation-problème.
L’acte de mesurer consiste à déterminer la mesure d’un attribut quelconque d’un objet, c’est-à-dire à donner un
ordre de grandeur à l’attribut en le quantifiant en fonction d’une unité de mesure.
Selon la situation, on utilise généralement l’une des stratégies ci-dessous pour déterminer une mesure :
- comparer et ordonner;
- juxtaposer des unités de mesure;
- utiliser un instrument de mesure;
- appliquer une formule.
Le choix de la stratégie dépend du contexte, de l’utilisation que l’on veut faire de la mesure, du degré de précision recherché et des instruments de mesure disponibles.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 87-89.
Utiliser un instrument de mesure
Un grand nombre d’instruments de mesure (par exemple, règle, thermomètre, balance) ont été conçus pour déterminer la mesure de divers attributs en fonction d’unités de mesure conventionnelles. Même si cette stratégie permet d’obtenir rapidement une mesure, elle requiert toutefois, de la part de la personne qui l’utilise, un bon sens de la mesure et une bonne capacité d’abstraction. Afin d’aider les élèves à comprendre l’importance de ces instruments et la façon de les utiliser correctement, le personnel enseignant peut leur proposer d’en fabriquer un.

« Les élèves comprendront probablement mieux le fonctionnement des instruments de mesure s’ils fabriquent des instruments de mesure simples basés sur des modèles d’unités qui leur sont familiers. […] Il est essentiel que les élèves comparent le dispositif non conventionnel avec l’instrument classique. Si les élèves n’ont pas l’occasion de faire cette comparaison, ils risquent de ne pas comprendre que ces deux instruments permettent d’arriver au même résultat. »
(Van de Walle et Lovin, 2008a, p. 272)
Au cycle moyen, il importe que les élèves apprennent à utiliser certains des instruments de mesure usuels dans
différents contextes tels que ceux énumérés dans le tableau ci-dessous en tenant compte du degré de précision
recherché et de l’importance de l’exactitude de la mesure.
|
Attribut |
Instruments |
|
Longueur |
|
|
Masse |
|
|
Capacité |
|
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 93-94.
CONNAISSANCE : PRÉFIXES MÉTRIQUES
Le système métrique va de pair avec le système de base dix. Chaque système renforce l’autre et contribue à la visualisation de l’autre système.
Les mêmes préfixes métriques s’appliquent à tous les attributs (sauf le temps) et désignent l’ordre de grandeur entre les unités de mesure. Pour toute unité de mesure métrique, chaque unité est 10 fois plus petite que l’unité précédente et 10 fois plus grande que l’unité suivante.
Bien que les préfixes métriques ne soient pas tous utilisés couramment au Canada, la compréhension de ce système aide à établir le lien avec la valeur de position des chiffres dans les nombres décimaux.
Préfixes métriques et relation à la valeur de position
| Préfixe métrique | kilo- | hecto- | déca- | Aucun préfixe | déci- | centi- | milli- |
|---|---|---|---|---|---|---|---|
| Valeur unitaire | 1000 unités | 100 unités | 10 unités | 1 unité | \(\frac{1}{10}\) d'unité | \(\frac{1}{100}\) d'unité | \(\frac{1}{1000}\) d'unité |
| Valeur de position | unité de mille | centaine | dizaine | unité | dixième | centième | millième |
Source: Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
CONNAISSANCE : UNITÉS DE MESURE MÉTRIQUES
Le monde scientifique a universellement recours au SI ou système international d’unités parce que ce système utilise des préfixes normalisés qui facilitent la compréhension des mesures et des conversions. Les unités métriques sont les unités conventionnelles de tous les pays du monde, sauf trois.
Source: Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Symboles et unités de mesure métriques de la longueur, de la masse et de la capacité
| km | kilomètre | hm | hectomètre | dam | décamètre | m | mètre | dm | décimètre | cm | centimètre | mm | millimètre |
| kg | kilogramme | hg | hectogramme | dag | décagramme | g | gramme | dg | décigramme | cg | centigramme | mg | milligramme |
| kl | kilolitre | hl | hectolitre | dal | décalitre | l | litre | dl | décilitre | cl | centilitre | ml | millilitre |
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 67.
CONNAISSANCE : ATTRIBUT LONGUEUR
La longueur est le terme général utilisé pour désigner toute grandeur d’un espace à une dimension que l’on mesure à l’aide d’un étalon.
Une longueur peut désigner :
- la grandeur d’un segment, c’est-à-dire la distance entre deux points;
- la distance entre deux droites parallèles ou deux plans parallèles;
- un périmètre;
- une hauteur, une profondeur, une épaisseur, une largeur, une taille.
Note : Pour certaines et certains élèves, ces différents termes associés à la longueur peuvent prêter à confusion.
Exemple
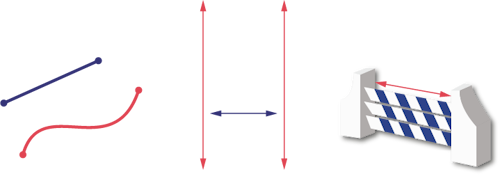 image Il y a trois symboles. Le premier est composé d’un trait droit et d’un
trait ondulé. Le
deuxième est composé d'un ensemble de traits verticaux et d’un trait horizontal qui identifie la distance entre
les traits. Le troisième est d’une clôture d’une hauteur de trois planches. Il y a un trait qui dénote la
longueur des planches.
image Il y a trois symboles. Le premier est composé d’un trait droit et d’un
trait ondulé. Le
deuxième est composé d'un ensemble de traits verticaux et d’un trait horizontal qui identifie la distance entre
les traits. Le troisième est d’une clôture d’une hauteur de trois planches. Il y a un trait qui dénote la
longueur des planches.

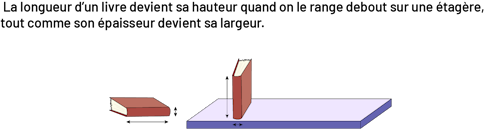 image Deux
images: la première est d’un livre posé horizontalement. Une ligne pointillée mesure le côté le plus long du
livre et une autre mesure l’épaisseur. La deuxième image est d’un livre posé verticalement sur une étagère. Une
ligne pointillée mesure le côté le plus long du livre et une autre mesure l’épaisseur.
image Deux
images: la première est d’un livre posé horizontalement. Une ligne pointillée mesure le côté le plus long du
livre et une autre mesure l’épaisseur. La deuxième image est d’un livre posé verticalement sur une étagère. Une
ligne pointillée mesure le côté le plus long du livre et une autre mesure l’épaisseur.
Source: Fiche de la 4e à la 6e année_Attribut longueur, p. 2.
CONNAISSANCE : ATTRIBUT MASSE
La masse désigne la quantité de matière d’un objet.
Seul le type de matière qui constitue un objet
influence sa masse. Ainsi, la masse d’un objet ne varie pas en fonction de l’endroit sur la Terre (ou dans l’espace)
où il est situé.
On détermine la masse d’un objet à l’aide, par exemple, d’une balance à triple fléau ou
d’une balance à deux plateaux.
Note : Il ne faut pas confondre masse et
poids. Le poids d’un objet désigne la force exercée sur cet objet par un corps céleste. Il est déterminé à
l’aide d’un dynamomètre et il est exprimé en newtons (N). Le poids d’un objet varie selon sa masse et selon
l’endroit sur la Terre (ou dans l’espace) où il est situé.
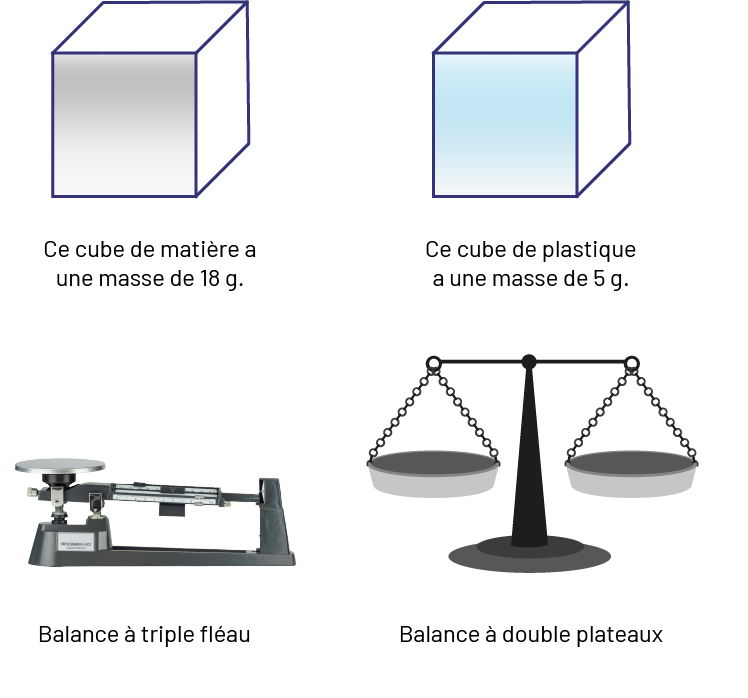 image Il y
a quatre illustrations: un cube de matière, un cube de plastique, une balance à triple fléau, et une balance à
doubles plateaux. Sous le premier cube est écrit: ce cube de matière a une masse de 18 grammes. Sous le deuxième
cube est écrit: ce cube de plastique a une masse de cinq grammes. Sous la première balance est écrite: balance à
triple fléau. Sous la deuxième balance est écrit: balance à doubles plateaux.
image Il y
a quatre illustrations: un cube de matière, un cube de plastique, une balance à triple fléau, et une balance à
doubles plateaux. Sous le premier cube est écrit: ce cube de matière a une masse de 18 grammes. Sous le deuxième
cube est écrit: ce cube de plastique a une masse de cinq grammes. Sous la première balance est écrite: balance à
triple fléau. Sous la deuxième balance est écrit: balance à doubles plateaux.
Source: Fiche de la 4e à la 6e année_Attribut masse, p. 2.
CONNAISSANCE : ATTRIBUT CAPACITÉ
La capacité d’un contenant désigne la quantité maximale d’une substance donnée qu’il est possible de mettre à l’intérieur du contenant. Lorsque la substance donnée remplit complètement le contenant, la capacité équivaut au volume intérieur du contenant.
 image Trois images: Un poisson dans un aquarium; un cylindre contenant
trois balles de tennis et un cylindre rempli d’eau; et une boîte en carton. À côté de l’image de l’aquarium est
écrit: la capacité ou le volume de cet aquarium est de deux litres. À côté de l’image, des cylindres, on peut lire:
ce cylindre a une capacité de trois balles de tennis et un volume intérieur de 750 millilitres. À côté de l’image de
la boîte en carton est écrit: Cette boîte a une capacité ou un volume intérieur de mille 200 centimètres
cubes.
image Trois images: Un poisson dans un aquarium; un cylindre contenant
trois balles de tennis et un cylindre rempli d’eau; et une boîte en carton. À côté de l’image de l’aquarium est
écrit: la capacité ou le volume de cet aquarium est de deux litres. À côté de l’image, des cylindres, on peut lire:
ce cylindre a une capacité de trois balles de tennis et un volume intérieur de 750 millilitres. À côté de l’image de
la boîte en carton est écrit: Cette boîte a une capacité ou un volume intérieur de mille 200 centimètres
cubes.
Source: Fiche de la 4e à la 6e année_Attribut capacité, p. 2.
