E2.2 Use metric prefixes to describe the relative size of different metric units, and choose appropriate units and tools to measure length, mass, and capacity.
Skill: Using Metric Prefixes to Describe the Relative Size of Different Metric Units
When students have a good grasp of the concept of an inverse relationship between the number of units required to determine a measurement and the size of that unit, they can more easily understand and establish relationships between some of the standard units.
In order for students to develop an understanding of these relationships, teachers must provide learning situations that allow them to both make sense of standard units and explore different strategies for converting from one unit to another. These strategies are based on the recognition that any unit can be expressed:
- as a multiple of a smaller unit of measurement (for example, one metre equals 1000 millimetres, one minute equals 60 seconds);
- as a fraction of a larger unit of measurement (for example, one metre is \(\frac{1}{1000}\) of a kilometre, one minute is \(\frac{1}{60}\) of an hour).
Relationships Between Units of Length, Mass, and Capacity
The fact that the various standard units associated with length, mass, and capacity are part of a decimal system of units is used to establish equivalence relationships between these units. For example, since the gram (g) is 10 times larger than the decigram (dg) and 10 times smaller than the decagram (dag), the following equivalence relationships can be established: 1 g = 10 dg, 1 g = 0.1 dag. Students should have a number of different learning experiences with concrete materials in order to develop a good understanding of these equivalence relationships. In order to be able to move easily from one unit to another, students must also understand the concept of inverse relationship.
Example 1
The teacher gives each team a tape measure and asks students to cover a tenth of it with a cardboard box, and then asks the following questions:
- What is a tenth of a metre? (1 dm, 10 cm, or 100 mm)
- What relationships can be established between the metre, the centimetre and the millimetre? (1 m = 100 cm, 1 cm = 10 mm, 1 m = 1000 m)
Note: The reasoning that makes it possible to establish these relationships is based on the concept of transitivity (for example, if a m is 100 times bigger than a cm, and a cm is 10 times bigger than a mm, then a m is 1000 bigger than a mm) , and can then encourage students to discover other relationships between units of length by asking them to cover one-tenth of a decimetre, one-tenth of a centimetre, one-hundredth of a metre, or even one-hundredth of a decimetre.
Example 2
Ask students to pour one liter of water into a graduated cylinder and to record the volume of water in the cylinder in centilitres and millilitres. Point out the following equivalences: 1 L = 100 cL, 1 L = 1000 mL. Prompt students to apply their understanding of the inverse relationship to establish relationships between the units used by asking questions such as:
- Why is the number corresponding to the measurement of the volume of water in the cylinders smaller when the volume is expressed in centilitres than when it is expressed in millilitres? (The centilitre is larger than the millilitre, so fewer centilitres than millilitres are needed to represent the same volume of water.)
- How many times fewer centilitres than millilitres of water are there in the graduated cylinder? (The volume of water in the graduated cylinder was recorded as 1000 mL or 100 cL, so there are 10 times fewer centilitres than millilitres of water in the graduated cylinder.)
- Is the centilitre much larger than the millilitre? How do you know? (Since the number of centilitres of water in the cylinder is 10 times smaller than the number of millilitres, we can conclude that the centilitre is 10 times larger than the millilitre.)
- How can you symbolically describe the relationship between centilitres and millilitres? (1 cL = 10 mL)
Prompt students to demonstrate their understanding of unit relationships by applying the same type of reasoning to another situation. For example, point out that the decilitre is a unit 10 times larger than the centilitre, then ask students:
- How many decilitres of water do you think are in the graduated cylinder? Why? (We know that there are 100 cL of water in the graduated cylinder. Since the decilitre is 10 times larger than the centilitre, the number of decilitres of water in the graduated cylinder must be 10 times smaller than 100. There must therefore be 10 dL of water in the graduated cylinder.)
As students explore such learning experiences, teachers should encourage them to apply their understanding of the relationships among the units. For example, with the understanding that a millimetre is one thousandths of a m or 1 mm = 0.001 m, ask students to make a conjecture about how many litres are in a millilitre. Then support them in formulating a generalization. For example, the prefix milli- placed in front of a unit designates a measurement equivalent to one thousandth of that unit, such as (1 mg = 0.001 g).
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Mesure, p. 64-66.
Skill: Choosing the Appropriate Unit and Measurement Tool
The act of measuring involves choosing an appropriate non-standard or standard unit to measure an attribute of an object. In order to do this, it is important to choose a unit that reflects the attribute to be measured and that is appropriate to the situation. In addition, it is generally preferable to use a single unit. Finally, it is also important that the choice of unit takes into account the degree of accuracy of the measurement sought (for example, a mass measurement to the nearest kilogram or gram).
When first exploring an attribute of an object, it is best for teachers to encourage students to choose a non-standard unit, so that they can focus on the meaning of the attribute and how it might be measured. Later, they can point out the limitations of the non-standard unit and the advantages of using a standard unit.
Example
A Grade 4 teacher asks students to determine the area of an exercise mat. The teacher presents students with a variety of objects (for example, circular tokens, algebra tiles, sticky notes, smartphone cases, large cardstock sheets, balls) and asks them to indicate, for each, whether the object is a good choice of unit for this task and to explain their answer. The table below provides examples of possible answers.
|
Object |
Possible Answer |
|
Circular token |
This is not a good choice because its circular shape does not lend itself well to measuring the area of a rectangular surface. |
|
Algebra tile Sticky note |
The rectangular shape of these two objects does reflect the attribute to be measured. However, since it would take a very large number of each of these objects to cover the mat, they are not the best choices as a standard object. |
|
Smartphone case Large cardstock sheet |
Each of these two objects is a good choice of a non-standard unit because they are easy to use to cover the mat to determine its area. It is important to note that in the case of a smartphone case, the area of one of the faces is used as the unit. |
|
Ball |
This is not a good choice because its curved surface does not lend itself to measuring the area of the mat. |
To ensure that students understand the meaning of a unit, the teacher asks a few students to demonstrate how the smartphone case and large cardstock sheet could be used to determine the area of the carpet. Students then demonstrate how the carpet can be covered using each of these objects.
The teacher then prompts students to think about the disadvantages of using these units to determine the area of the mat by asking questions such as:
- If I told you that the area of the mat is equal to the area of six large cardstock sheets, would you have a good picture of the area of the mat? Justify your answer. (Yes, but only to the extent that we have a good mental picture of the cardstock sheet used. Otherwise, it is not possible to have a good picture of the area of the mat.)
- When buying fabric to cover the mat, would it be helpful to tell the salesperson that the area of the mat is the area of 36 sides of a smartphone case? Why? (No, because that is not a unit that is commonly used to describe a quantity of fabric.)
In repeating the activity using square centimetres or square metres as units, the teacher can point out that these units are called standard units because they are commonly used by many people and therefore have the advantage of making the communication of the measurement clear. The teacher can also point out that the standard units chosen must also reflect the attribute to be measured, must be appropriate to the situation, and must preferably be the same in order to be useful and appropriate for solving the problem situation.
The act of measuring consists of determining the measurement of an attribute of an object, namely, giving an order of size to the attribute by quantifying it in terms of a unit.
Depending on the situation, one of the following strategies is typically used to determine a measure:
- comparing and ordering;
- juxtaposing units;
- using a measuring tool;
- applying a formula.
The choice of strategy depends on the context, the intended use of the measurement, the degree of accuracy sought, and the measuring tools available.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Mesure, p. 87-89.
Using a Measuring Tool
Many measuring tools (for example, ruler, scale) have been designed to determine the measurement of various attributes in terms of standard units. Although this strategy provides a quick measurement, it requires the user to have a good sense of measurement and abstract thinking. To help students understand the importance of these measuring tools and how to use them correctly, teachers can suggest that they make one.

In the junior grades, it is important that students learn to use some of the common measuring tools in a variety of contexts such as those listed in the table below, taking into account the degree of precision sought and the importance of accuracy of measurement.
|
Attribute |
Measuring Tools |
|
Length |
|
|
Mass |
|
|
Capacity |
|
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Mesure, p. 93-94.
Knowledge: Metric Prefixes
The metric system goes hand in hand with the base ten system, each system reinforcing the other and contributing to the visualization of the other system.
The same metric prefixes apply to all attributes (except time) and designate the order of size between units. For any metric unit, each unit is 10 times smaller than the previous unit (to the left on the chart) and 10 times larger than the next unit (to the right on the chart).
Although not all metric prefixes are commonly used in Canada, understanding this system helps to make the connection to the positional value of digits in decimal numbers.
Metric Prefixes and Relation to the Position Value
| Metric Prefix | kilo- | hecto- | deca- | No prefix | deci- | centi- | milli- |
|---|---|---|---|---|---|---|---|
| Unit Value | 1000 units | 100 units | 10 units | 1 unit | \(\frac{1}{10}\) unit | \(\frac{1}{100}\) unit | \(\frac{1}{1000}\) unit |
| Place Value | thousand | hundred | ten | one | one tenth | one hundredth | one thousandth |
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
Knowledge: Metric Units
The metric system is universally used among scientists because it uses standard prefixes for measurements and conversions. Metric units for measurement are the standard unit in all but three countries in the world.
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
Symbols and Metric Units for Length, Mass, and Capacity
| km | kilometre | hm | hectometre | dam | decametre | m | metre | dm | decimetre | cm | centimetre | mm | millimetre |
| kg | kilogram | hg | hectogram | dag | decagram | g | gram | dg | decigram | cg | centigram | mg | milligram |
| kL | kilolitre | hL | hectolitre | daL | decalitre | L | litre | dL | decilitre | cL | centilitre | mL | millilitre |
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Mesure, p. 67.
Knowledge: Length
Length is a measure in a one-dimensional space.
A length can refer to:
- the size of a line segment, namely, the distance between two points;
- the distance between two parallel lines or two parallel planes;
- a perimeter;
- a height, a depth, a thickness, a width, a height (of a person).
Note: For some students, these different terms associated with length may be confusing.
Example
 image There are three symbols. The first is composed of a straight line and a wavy line. The second is composed of a set of vertical lines and a horizontal line that identifies the distance between the lines. The third is a fence with a height of three boards. There is a line that denotes the length of the planks.
image There are three symbols. The first is composed of a straight line and a wavy line. The second is composed of a set of vertical lines and a horizontal line that identifies the distance between the lines. The third is a fence with a height of three boards. There is a line that denotes the length of the planks.
Perimeter refers to the length around a two-dimensional shape or any three-dimensional object.
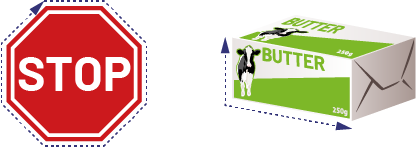
The length of a book becomes its height when stored upright on a shelf, just as its thickness becomes its width.
 Two images: the first is of a book laid horizontally. A dotted line measures the longest side of the book and another measures the thickness. The second image is of a book placed vertically on a shelf. One dotted line measures the longest side of the book and another measures the thickness.
Two images: the first is of a book laid horizontally. A dotted line measures the longest side of the book and another measures the thickness. The second image is of a book placed vertically on a shelf. One dotted line measures the longest side of the book and another measures the thickness.Source: translated from Fiche de la 4e à la 6e année, Attribut longueur, p. 2.
Knowledge: Mass
Mass refers to the amount of matter in an object.
Only the type of matter that makes up an object influences its mass. Thus, the mass of an object does not vary depending on where on Earth (or in space) it is located.
The mass of an object is determined using, for example, a triple-beam scale or a two-pan balance scale.
Note: Mass should not be confused with weight. The weight of an object refers to the force exerted on that object by a celestial body. It is determined using a dynamometer and is expressed in newtons (N). The weight of an object varies depending on its mass and the place on Earth (or in space) where it is located.
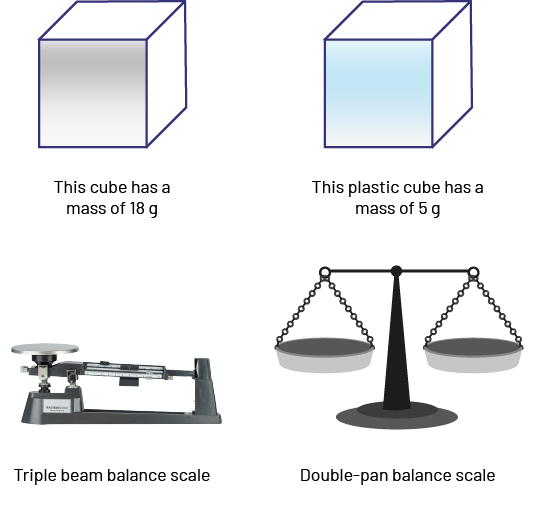 image There are four illustrations: a cube of matter, a plastic cube, a triple beam scale, and a double pan scale. Under the first cube is written: this cube of matter has a mass of 18 grams. Under the second cube is written: this cube of plastic has a mass of five grams. Under the first scale is written: triple beam scale. Under the second scale is written: double scale.
image There are four illustrations: a cube of matter, a plastic cube, a triple beam scale, and a double pan scale. Under the first cube is written: this cube of matter has a mass of 18 grams. Under the second cube is written: this cube of plastic has a mass of five grams. Under the first scale is written: triple beam scale. Under the second scale is written: double scale.
Source: translated from Fiche de la 4e à la 6e année, Attribut masse, p. 2.
Knowledge: Capacity
The capacity of a container is the greatest amount that the container can hold. When the container is completely filled, the capacity is equal to the interior volume of the container.
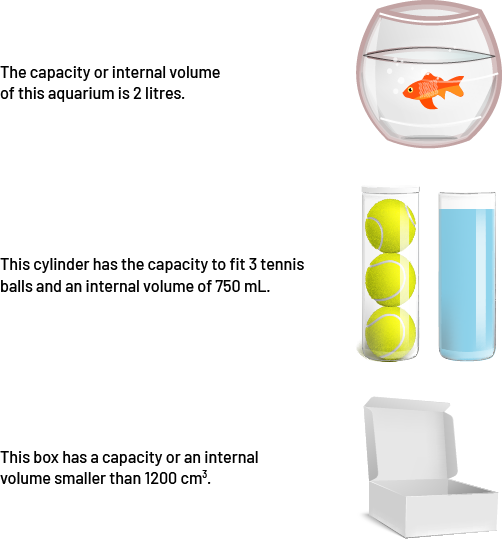 image Three pictures: A fish in an aquarium; a cylinder containing three tennis balls and a cylinder filled with water; and a cardboard box. Next to the picture of the aquarium is written: the capacity or volume of this aquarium is two liters. Next to the picture of the cylinders is written: this cylinder has a capacity of three tennis balls and an interior volume of 750 milliliters. Next to the picture of the cardboard box is written: This box has a capacity or interior volume of one thousand 200 cubic centimeters.
image Three pictures: A fish in an aquarium; a cylinder containing three tennis balls and a cylinder filled with water; and a cardboard box. Next to the picture of the aquarium is written: the capacity or volume of this aquarium is two liters. Next to the picture of the cylinders is written: this cylinder has a capacity of three tennis balls and an interior volume of 750 milliliters. Next to the picture of the cardboard box is written: This box has a capacity or interior volume of one thousand 200 cubic centimeters.
Source: translated from Fiche de la 4e à la 6e année, Attribut capacité, p. 2.
