E2.3 Résoudre des problèmes associés à la durée en se servant des relations entre différentes unités de mesure de temps.
HABILETÉ : RÉSOUDRE DES PROBLÈMES ASSOCIÉS À LA DURÉE
L’addition, la soustraction et différentes stratégies peuvent être utilisées pour calculer la durée. Une droite numérique ouverte peut être utilisée pour suivre les divers repères de la durée et les unités de temps correspondantes.
Exemple
Déterminer combien de temps s’écoule entre 8 h 45 et 15 h 15 (6 heures et 30 minutes).
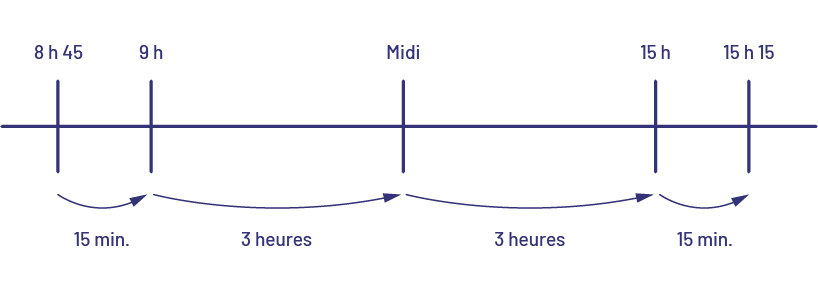image Une
ligne horizontale qui démarque le temps qui s’écoule entre huit heures 45 et neuf heures, entre neuf heures et midi,
entre midi et 15 heures, et entre 15 heures et 15 heures et quart. Les intervalles sont dénotés par des flèches: la
première est de 15 minutes, la deuxième est de trois heures, la troisième est de trois heures, et la quatrième est de
quinze minutes.
Les problèmes de durée concernent souvent le passage d’une unité de temps à l’autre. Il faut comprendre les relations entre les unités de temps (année, mois, semaine, jour, heure, minute et seconde), y compris les notions d’avant-midi et d’après-midi sur une horloge de 24 heures.
Source: Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
CONNAISSANCE : DURÉE
Le temps comme durée désigne l’intervalle entre deux moments d’un événement. C’est un attribut qui se mesure, par exemple, à l’aide d’un chronomètre, d’une horloge ou d’un calendrier.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 43.
CONNAISSANCE : RELATIONS ENTRE DIFFÉRENTES UNITÉS DE MESURE DE TEMPS
Relation inverse
Le nombre d’unités requis pour déterminer la mesure d’un attribut est inversement proportionnel à la grandeur de l’unité de mesure utilisée. Autrement dit :
- plus l’unité de mesure utilisée est petite, plus le nombre d’unités requis pour déterminer la mesure de l’attribut est grand;
- plus l’unité de mesure utilisée est grande, plus le nombre d’unités requis pour déterminer la mesure de l’attribut est petit.
Par exemple, si on mesure la durée d’une même activité une première fois en minutes et une deuxième fois en secondes, on aura un plus grand nombre de secondes que de minutes étant donné que la seconde est une unité de mesure plus petite que la minute. Quoique le concept de relation inverse puisse sembler évident dans ce genre de situation, il pose problème pour plusieurs élèves qui connaissent bien les situations de relation directe (par exemple, plus grande est la distance à parcourir en voiture, plus grande sera la durée du trajet). Afin de les aider à bien comprendre ce concept, le personnel enseignant doit leur présenter diverses situations concrètes de mesure qui les incitent à établir ce lien.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 60.
Relations entre des unités de mesure conventionnelles
Lorsque les élèves saisissent bien le concept de relation inverse entre le nombre d’unités requis pour déterminer une mesure et la grandeur de cette unité, elles et ils peuvent plus facilement comprendre et établir des relations entre certaines des unités de mesure conventionnelles.
Pour que les élèves puissent développer une bonne compréhension de ces relations, le personnel enseignant doit leur proposer des situations d’apprentissage qui leur permettent à la fois de donner un sens aux unités de mesure conventionnelles et d’explorer différentes stratégies de conversion d’une unité à l’autre. Ces stratégies reposent sur la reconnaissance que toute unité de mesure peut être exprimée :
- en tant que multiple d’une unité de mesure plus petite (par exemple, un mètre équivaut à 1 000 millimètres, une minute équivaut à 60 secondes);
- en tant que fraction d’une unité de mesure plus grande (par exemple, un mètre équivaut à \(\frac{1}{1 000}\) de kilomètre, une minute équivaut à \(\frac{1}{60}\) d’une heure).
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 62-64.
Relations entre des unités de mesure de l’attribut temps
Au cycle moyen, les élèves devraient avoir l’occasion d’explorer et d’utiliser, dans le cadre de diverses activités quotidiennes, les relations entre les secondes et les minutes, ainsi que celles entre les activités présentées selon l’affichage sur 24 heures (par exemple, indiquer l’heure des récréations du matin et de l’après-midi selon l’affichage sur 24 heures). En ce qui a trait aux mesures de temps en années, en mois, en semaines, en jours, en heures, en minutes et en secondes, il est préférable d’aborder ces unités avec les élèves dans un contexte d’intégration des matières. Le personnel enseignant peut, par exemple, leur demander de situer, sur une ligne du temps, les routines des élèves pendant une semaine ou les étapes importantes de leur vie de leur naissance à aujourd’hui.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 68-69.