E2.3 Solve problems involving elapsed time by applying the relationships between different units of time.
Skill: Solving Problems Associated with Elapsed Time
Addition, subtraction, and different counting strategies can be used to calculate the difference between two dates or times. Open number lines (timelines) can be used to track the multiple steps and different units used to determine elapsed time.
Example
Determine how much time passes between 8:45 a.m. and 3:15 p.m. (6 hours and 30 minutes).
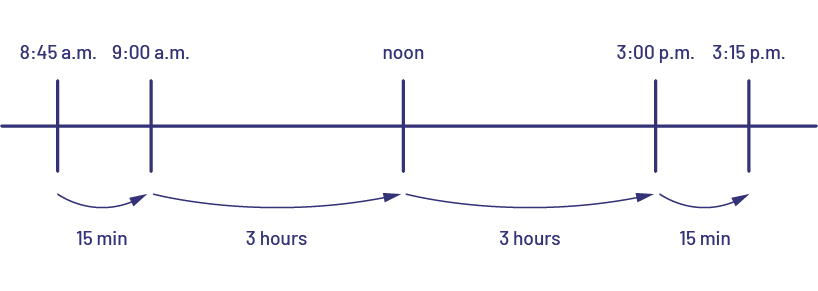image A horizontal line that marks the time between 8:45 and 9:00, 9:00 and 12:00, 12:00 and 15:00, and 15:00 and 15:15. The intervals are indicated by arrows: the first is 15 minutes, the second is three hours, the third is three hours, and the fourth is fifteen minutes.
Elapsed-time problems often involve moving between different units of time. This requires an understanding of the relationships between units of time (years, months, weeks, days, hours, minutes, seconds), including an understanding of a.m. and p.m. as conventions to convert the 24-hour clock into a 12-hour clock, as illustrated above.
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
Knowledge: Duration
Time as duration is the interval between two moments of an event and is an attribute that can be measured, for example, with a stopwatch, clock or calendar.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Mesure, p. 43.
Knowledge: Relationships Between Different Units of Time
Inverse Relationship
The number of units required to determine the measure of an attribute is inversely proportional to the size of the unit used. In other words:
- the smaller the unit used, the greater the number of units required to determine the measurement of the attribute;
- the larger the unit used, the smaller the number of units required to determine the measurement of the attribute.
For example, if the duration of the same activity is measured in minutes and is also measured in seconds, there will be more seconds than minutes because the second is a smaller unit than the minute. Although the concept of an inverse relationship may seem obvious in this type of situation, it is problematic for many students who are familiar with direct relationship situations (for example, the greater the distance to be travelled by car, the greater the duration of the trip). In order to help them understand this concept, teachers should present them with a variety of concrete measurement situations that encourage them to make this connection.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Mesure, p. 60.
Relationships Between Standard Units
When students have a good grasp of the concept of an inverse relationship between the number of units required to determine a measurement and the size of that unit, they can more easily understand and establish relationships between some of the standard units.
In order for students to develop an understanding of these relationships, teachers should provide learning experiences that allow them to both make sense of standard units and explore different strategies for converting from one unit to another. These strategies are based on the recognition that any unit can be expressed:
- as a multiple of a smaller unit (for example, one minute equals 60 seconds);
- as a fraction of a larger unit (for example, one minute is \(\frac{1}{60} \) of an hour).
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Mesure, p. 62-64.
Relationships Between Units of Time
In the junior grades, students should have opportunities to explore and use the relationships between seconds and minutes, as well as those between activities on the 24-hour clock, and a variety of daily activities (for example, indicating the time of morning and afternoon recesses on the 24-hour clock). For measurements of time in years, months, weeks, days, hours, minutes, and seconds, these units are best approached with students in the context of authentic contexts. For example, teachers can ask students to locate, on a timeline, the routines of students during a week or the milestones in their lives from birth to the present.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Mesure, p. 68-69.