La vue d'ensemble

À vue d'oeil...

un remaniement des guides d'enseignement efficace en mathématiques

FrançaisEnglish

E1.3 Tracer les vues de côté, de face et de dessus de divers objets et faire correspondre le dessin à l'objet.

Activité 1 : fais-moi un dessin 1

Prendre quelques prismes droits à base rectangulaire identiques (par exemple, des boîtes de papiers-mouchoirs) et les placer à la verticale sur certains pupitres. Demander aux élèves de dessiner les vues de face, de côté et de dessus des prismes. Mentionner aux élèves que, pour bien observer les vues de face et de côté, il est important de se placer de manière que les yeux soient au niveau de la surface du pupitre. Lorsque les élèves ont terminé, demander à une ou à un élève de dessiner les différentes vues d'un des prismes au tableau. Faire une mise en commun et s'assurer que toutes et tous les élèves sont d'accord avec les vues présentées et comprennent la façon de les obtenir.

Vue de côté :

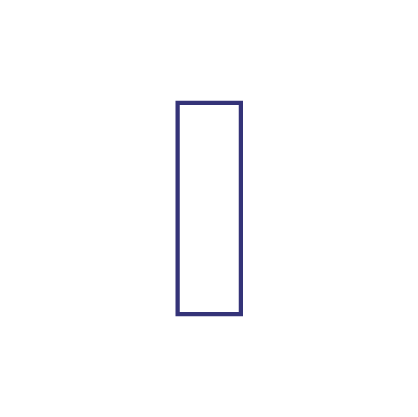
Un rectangle mince ayant deux ensembles de côtés parallèles, soit un plus court et un plus long. Le rectangle est vertical.

Vue de face :

Un rectangle épais ayant deux ensembles de côtés parallèles, soit un plus court et un plus long. Le rectangle est vertical.

Vue de dessus :

Un rectangle ayant deux ensembles de côtés parallèles, soit un plus court et un plus long. Le triangle est horizontal.

Note : Les vues de côté et de face sont interchangeables selon la position de l'élève par rapport à l'objet.

Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 104.

Activité 2 : trois vues valent mieux que deux!

Grouper les élèves en équipes de deux. Leur demander de construire une maquette quelconque en utilisant un nombre donné de cubes emboîtables (par exemple, 15 cubes). Les inviter à tracer les vues de face, de côté et de dessus de cette maquette.

Récupérer tous les dessins de vues et placer toutes les structures fabriquées au même endroit (par exemple, sur une table).

Remettre un dessin à chaque équipe en s’assurant de ne pas leur remettre leur propre dessin.

Inviter les équipes à trouver la structure correspondant aux vues de face, de côté et de dessus de leur feuille.

Note : Même avec trois vues, il est possible de construire deux maquettes qui ne sont pas parfaitement identiques.

Source : adapté de Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 92.

Activité 3 : que voit-on d'en haut?

Demander aux élèves de dessiner toutes les vues de dessus que pourrait avoir une structure formée de quatre cubes emboîtables liés les uns aux autres. Leur préciser qu'elles et ils doivent tenter de visualiser toutes les structures possibles et de dessiner les vues de dessus correspondantes sans utiliser de matériel concret. Grouper ensuite les élèves deux par deux et les inviter à comparer leurs réponses. Au besoin, leur permettre d'utiliser des cubes emboîtables pour vérifier les réponses.

Note : Les 11 vues de dessus ci-dessous sont possibles.

image 11 formes distinctes composées d’une série de carrés. La première est d’un carré unique. La deuxième est composée de deux carrés horizontaux mis à côtés. La troisième est composée de trois carrés horizontaux mis à côtés. La quatrième est composée de quatre carrés horizontaux mis à côtés. La cinquième est d’un carré composé de quatre carrés. La sixième est composée d’une série horizontale de trois carrés, et d’un carré sous le deuxième carré. La septième est composée de trois carrés formant un coin. La huitième est composée de quatre carrés, dont deux lignes horizontales de deux carrés chaque. La neuvième est composée de quatre carrés, dont deux lignes horizontales de deux carrés chaque. La dixième est composée d’une série horizontale de trois carrés, et d’un carré sous le premier carré. La onzième est composée d’une série horizontale de trois carrés, et d’un carré sous le troisième carré.

Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 93.

ACTIVITÉ 4 : FAIS-MOI UN DESSIN 2

Remettre aux élèves l'illustration d'une maquette. Leur demander de dessiner les vues de face, de côté et de dessus qui pourraient correspondre à la maquette. Grouper ensuite les élèves en équipes de deux et les inviter à comparer leurs réponses. Au besoin, leur permettre d'utiliser des cubes emboîtables pour vérifier les réponses.

Note : L'illustration permet de voir la maquette d'un seul angle de vue. Puisqu'elle pourrait être composée de plus de cubes que ceux que l'on voit dans l'illustration, les dessins des vues pourraient varier.

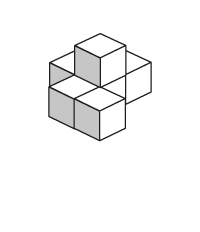
Une structure ayant une base de laquelle cinq cubes sont visibles, et un cube posé sur le centre de la base.

Exemple 1

Une structure ayant une base de laquelle cinq cubes sont visibles, d’une deuxième et troisième couche d’un cube, et d’une quatrième couche de deux cubes.

Exemple 2

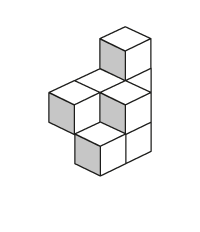
Une structure ayant une base de laquelle deux cubes sont visibles, une deuxième couche de quatre cubes visibles, et une troisième couche d’un cube.

Exemple 3

Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 93.