E1.1 Reconnaître les propriétés géométriques des triangles et construire divers types de triangles en utilisant des mesures d'angles ou de côtés données.
HABILETÉ : RECONNAÎTRE LES PROPRIÉTÉS GÉOMÉTRIQUES DES TRIANGLES
Les propriétés géométriques sont des attributs précis qui définissent une classe de figures planes ou de solides. Certaines propriétés géométriques des triangles sont :
- Tous les triangles possèdent trois côtés et trois angles.
- La longueur combinée de deux côtés d’un triangle, peu importe lesquels, est toujours supérieure à la longueur du troisième.
- La somme de la mesure des angles intérieurs d’un triangle équivaut toujours à 180° (par exemple, 70° + 60° + 50° = 180°).
- La somme de la mesure des angles extérieurs d’un triangle équivaut toujours à 360° (par exemple, 110° + 120° + 130° = 360°).
- La somme de la mesure d’un angle intérieur et de l’angle extérieur correspondant équivaut toujours à 180° (par exemple, 130° + 50° = 180°).
Les triangles peuvent être classés selon la longueur de leurs côtés ou selon la mesure de leurs angles.
Classement des triangles selon la longueur des côtés
Triangle équilatéral
Trois côtés congrus
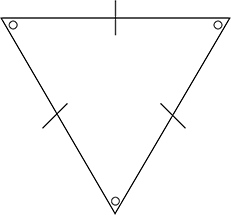
Triangle isocèle
Deux côtés congrus
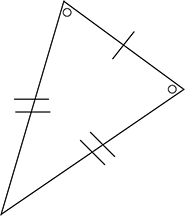
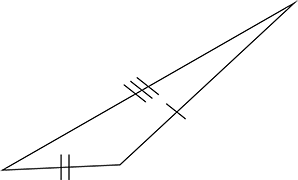
Triangle scalène
Trois côtes de différentes longueurs
Classement des triangles selon la mesure des angles
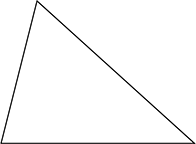
Triangle acutangle
Tous les angles sont inférieurs à 90° (trois angles aigus)
Triangle rectangle
Un angle de 90° (un angle droit)
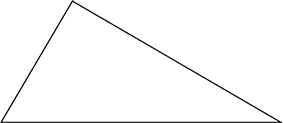
Triangle obtusangle
Un angle supérieur à 90° (un angle obtus)
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
HABILETÉ : TRACER UN TRIANGLE EN FONCTION DE SES CARACTÉRISTIQUES CONNUES ET INCONNUES
Il existe différentes techniques pour tracer un triangle en fonction de ses caractéristiques connues.
Lorsque la longueur de chaque côté est connue, mais non les mesures des angles, il est possible d'utiliser une règle et un compas pour tracer un triangle. Comme la distance entre tout point d'un cercle et son centre (le rayon) est constante, un triangle ayant un côté de 8 cm se trouve nécessairement sur un cercle ayant un rayon de cette longueur. Le sommet d'un triangle se situe à l'endroit où deux cercles se croisent.
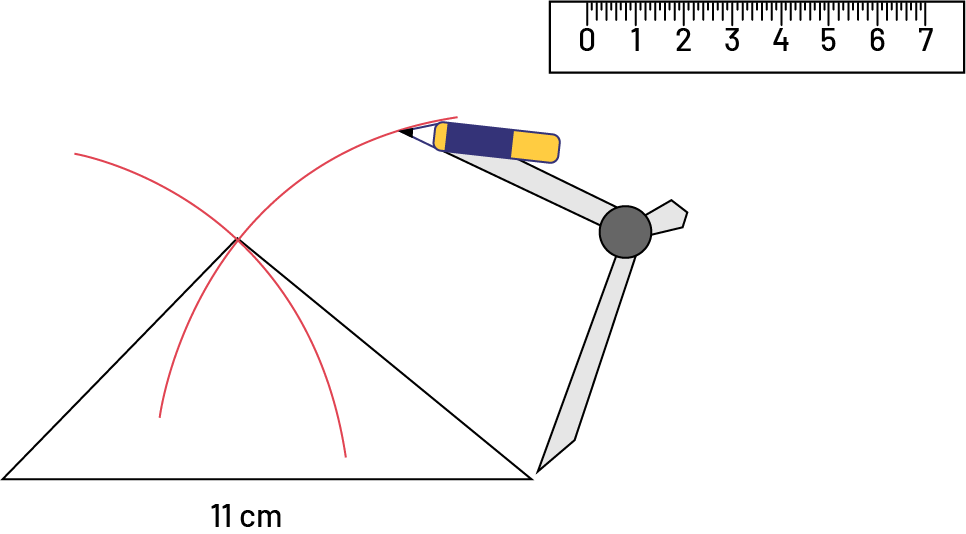
Lorsque la longueur d'un côté et les mesures des angles sont connues, il est possible de tracer le triangle à l'aide d'un rapporteur et d'une règle. Le sommet se situe à l'endroit où se croisent les droites qui partent des angles.
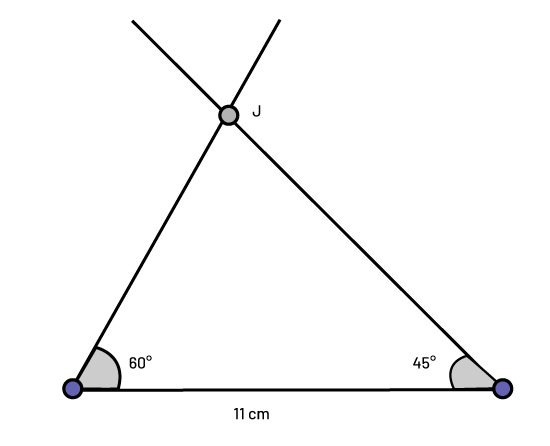
Il est possible de tracer un triangle en fonction de ses caractéristiques inconnues en se servant d'une application de géométrie dynamique de nombreuses manières, y compris en transformant des points et en créant des cercles.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
CONNAISSANCE : PROPRIÉTÉ GÉOMÉTRIQUE
Une propriété est une caractéristique particulière qui sert à définir une forme géométrique ou une famille de formes géométriques. Attention à ne pas confondre les propriétés et les attributs. Les attributs décrivent l'apparence physique d'une forme, comme sa taille, sa couleur et sa texture.
Exemple
Le nombre de côtés, les mesures des angles, le nombre de diagonales sont des exemples de propriétés.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 5.
