La vue d'ensemble

At a Glance...

The Guides for Effective Instruction in Mathematics Revised

FrançaisEnglish

E1.1 Identify geometric properties of triangles, and construct different types of triangles when given side or angle measurements.

Skill: Identifying the Geometric Properties of Triangles

Geometric properties are specific attributes that define a class of two-dimensional shapes or three-dimensional objects. Some geometric properties of triangles are:

  • All triangles have three sides and three angles.
  • The combined length of any two sides of a triangle is always greater than the length of the third.
  • The sum of the measurements of the interior angles of a triangle always equals 180° (for example, 70° + 60° + 50° = 180°).
  • The sum of the measurements of the exterior angles of a triangle always equals 360° (for example, 110° + 120° + 130° = 360°).
  • The sum of the measurement of an interior angle and the corresponding exterior angle is always 180° (for example 130° + 50° = 180°).

Triangles can be classified according to the length of their sides or the size of their angles.

Classification of Triangles According to the Length of the Sides

Equilateral Triangle

Three equal sides

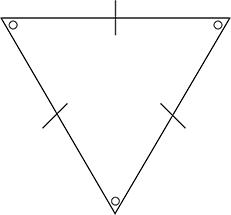
A triangle with three congruent sides and three equal angles.

Isosceles Triangle

Two equal sides

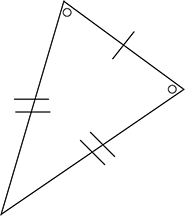
A triangle with two congruent sides and two equal angles, and a shorter side and a different angle.

Scalene Triangle

No equal sides

A triangle with three sides and three different angles.

Classification of Triangles According to the Measure of the Angles

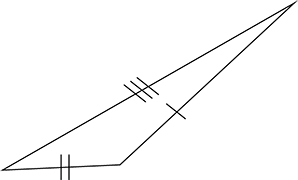
Acute Triangle

All angles are less than 90°

A triangle with three sides of different lengths and three acute angles.

Triangle Rectangle

One angle is 90°

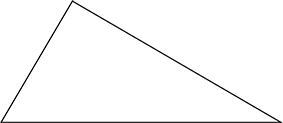
A triangle with two sides of the same length and one side shorter, and with two acute angles and one right angle.

Obtuse Triangle

An angle greater than 90°

A triangle with two sides of the same length and one side shorter, and with two acute angles and one obtuse angle.

Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.

Skill: Drawing a Triangle According to Its Known and Unknown Characteristics

There are different techniques for constructing triangles depending on what is known and unknown.

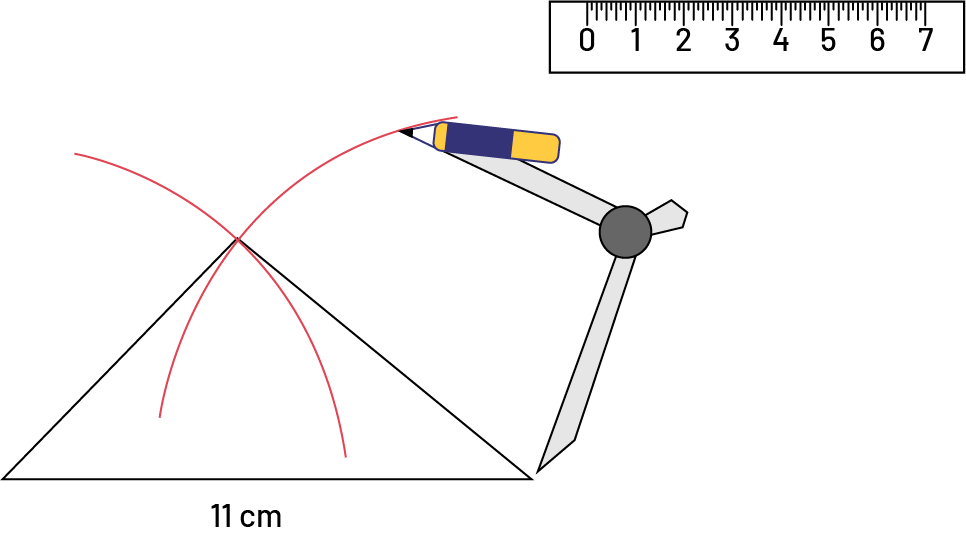
When all side lengths of a triangle are known but the angles are unknown, a ruler and compass can be used to construct the triangle. To do so, one could draw the length of one of the sides, then set the compass for the length of another side. The compass can then be put at one of the ends of the line and an arc drawn. Now the compass should be set to the length of the third side and set on the other end of the line to draw another arc. Where the two arcs intersect is the third vertex of the triangle (see the diagram below). The sides can be completed by drawing a line from the ends of the original line to the point of intersection.

A triangle 11 centimeters at the base. A compass extends from the base and marks an 'x' at the top of the triangle. In the upper right corner, there is a seven-centimeter or three-inch ruler.

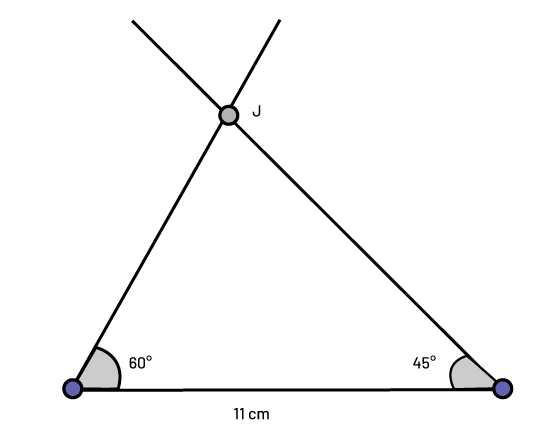
When one side length and two of the angles of a triangle are known, a protractor and a ruler can be used to construct the triangle. The unknown vertex is the point where the arms of the angles intersect:

A triangle of 11 centimeters at the base, having an angle of 60 degrees and an angle of 45 degrees. The third angle is demarcated at the point where the sides intersect by a 'j'.

Triangles can also be constructed using dynamic geometry applications in many ways, including by transforming points and by constructing circles.

Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.

Knowledge: Geometric Property

A property is a particular characteristic that is used to define a geometric shape or object or a family of geometric shapes or objects. Be careful not to confuse properties and attributes. Attributes describe the physical appearance of a shape or object, such as its size, color and texture.

Example

The number of sides, the measurements of angles, and the number of diagonals are examples of properties.

Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Géométrie et sens de l'espace, Document d'appui, Fascicule 1, p. 5.