E2.5 Utiliser les relations entre l'aire des rectangles, des parallélogrammes et des triangles afin de développer des formules pour l'aire d'un parallélogramme et d'un triangle, et résoudre des problèmes connexes.
HABILETÉ : UTILISER LES RELATIONS ENTRE LES AIRES DES RECTANGLES, DES PARALLÉLOGRAMMES ET DES TRIANGLES AFIN DE DÉVELOPPER DES FORMULES POUR L'AIRE D'UN PARALLÉLOGRAMME ET L'AIRE D'UN TRIANGLE
Relations entre des attributs
L'exploration des relations entre des attributs permet aux élèves de développer une meilleure compréhension des formules usuelles utilisées pour déterminer l'aire de certaines figures planes ou le volume de certains solides, et de les appliquer en toute connaissance de cause dans diverses situations de résolution de problèmes.
Relations entre les attributs longueur et aire
Le personnel enseignant doit présenter aux élèves des activités de mesure qui leur permettent d'établir une relation entre les dimensions (base et hauteur) de certaines figures planes (rectangle, parallélogramme et triangle) et leur aire. Les élèves doivent construire les concepts de « hauteur » et de « base » par l'intermédiaire d'activités qui les aident à comprendre que n'importe lequel des côtés d'une figure peut être la base et que, pour chaque base, il y a une « hauteur » correspondante.
Rectangle
Les élèves devraient commencer par établir la relation entre les dimensions d'un rectangle et son aire. Elles et ils pourront ensuite utiliser cette relation pour établir les dimensions du parallélogramme et celles du triangle. Lorsqu'il est question de rectangles, il est aussi question de carrés, puisque tous les carrés font partie de l'ensemble des rectangles.
Exemple
Le personnel enseignant remet aux élèves une série de rectangles, ainsi que le transparent d'une grille quadrillée en centimètres carrés. Les élèves posent le transparent sur chaque rectangle, déterminent la mesure de la base, de la hauteur et de l'aire de la figure et notent les résultats dans un tableau.

|
Rectangle |
Base |
Hauteur |
Aire |
|
Bleu |
6 cm |
1 cm |
6 cm2 |
|
Jaune |
4 cm |
3 cm |
12 cm2 |
|
Rouge |
2,5 cm |
4 cm |
10 cm2 |
Au moment de l'échange mathématique, le personnel enseignant fait ressortir les différentes stratégies qu'ont utilisées les élèves pour déterminer l'aire.
- J'ai placé le transparent sur le rectangle et j'ai dénombré les carrés qui recouvrent sa surface.
- L'aire de chaque rectangle est comme une disposition rectangulaire. J'ai dénombré les carrés dans une rangée et j'ai multiplié par le nombre de rangées. Dans le rectangle jaune, par exemple, il y a 3 rangées de 4 carrés chacune. J'ai dénombré les carrés dans une colonne et j'ai multiplié par le nombre de colonnes. Dans le rectangle rouge, par exemple, il y a 2,5 colonnes de 4 carrés chacune.
Le personnel enseignant incite ensuite les élèves à formuler une généralisation relative à la relation qui existe
entre les dimensions d'un rectangle et son aire. La formulation se fait d'abord en mots (l'aire du rectangle est
égale au produit de la mesure de sa base et de sa hauteur), puis à l'aide de symboles mathématiques (A =
b × h).
La formule de l'aire d'un rectangle est l'une des premières qu'apprennent les élèves. Elle se présente généralement sous la forme A = L × l et se lit « l'aire est égale à la longueur multipliée par la largeur ». Si l'on pense à d'autres formules d'aire, il existe une expression équivalente, mais dont le concept sous-jacent est plus unificateur. Il s'agit de la formule A = b × h, qui se lit « l'aire est égale à la base multipliée par la hauteur ». Cette formulation en fonction de la base et de la hauteur peut être généralisée à tous les parallélogrammes et facilite l'élaboration de formules de l'aire d'un triangle et [celui]d'un trapèze (J. Van de Walle et L. H. Lovin, L'enseignement des mathématiques : L'élève au centre de son apprentissage, tome 3, 2008, p. 274, cités dans Ministère de l'Éducation de l'Ontario, Guide d'enseignement efficace des mathématiques, de la 4e à la 6e année – Mesure, 2010, p. 72).
Mesure de la longueur, le diamètre, la circonférence, le périmètre et l’aire
 Description de la vidéo
Description de la vidéo
Description à venir
Parallélogramme
Lorsque les élèves ont bien compris la façon de déterminer l'aire d'un rectangle, ainsi que le sens de la formule
usuelle correspondante (A = b × h), elles et ils peuvent utiliser ces connaissances pour
établir la relation entre les dimensions d'un parallélogramme et son aire.
La plupart des étapes de passage de la formule d'aire d'une figure à une autre sont des démarches de découverte, de construction, permettant l'induction : à partir de ce qu'[elle ou] il connaît, l'enfant combine, recherche et construit la formule d'aire qu'[elle ou] il ne connaît pas (X. Roegiers, Les mathématiques à l'école primaire, tome 2, 2000, p. 134, cité dans Ministère de l'Éducation de l'Ontario, Guide d'enseignement efficace des mathématiques, de la 4e à la 6e année – Mesure, 2010, p. 175).
Exemple
Le personnel enseignant groupe les élèves en équipes de deux. Il remet à chaque équipe un parallélogramme, dont la mesure de la base et celle de la hauteur correspondent à des valeurs entières (par exemple, base de 4 cm et hauteur de 5 cm), ainsi que le transparent d'une grille quadrillée en centimètres carrés. Elle ou il demande aux élèves si elles et ils peuvent trouver une façon de déterminer l'aire du parallélogramme.
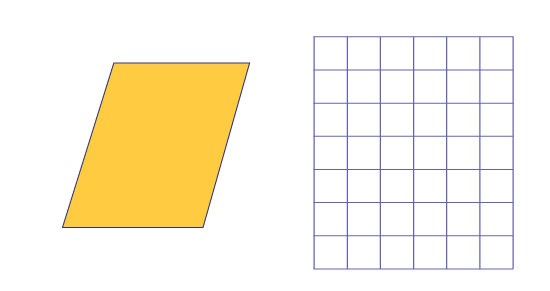
Au moment de l'échange mathématique, le personnel enseignant fait ressortir les différentes stratégies qu'ont
utilisées les élèves pour déterminer l'aire.
Exemple :
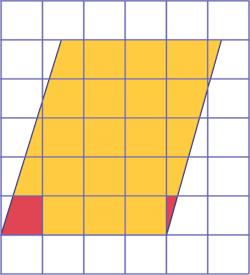
- Nous avons placé le transparent sur le rectangle et nous avons dénombré les carrés entiers. Puis, nous avons
remarqué que, pour chaque rangée, la partie de carré à gauche combinée à la partie de carré à droite donnait un
carré entier. Nous avons donc pu déterminer que l'aire du parallélogramme est égale à
20 cm2.
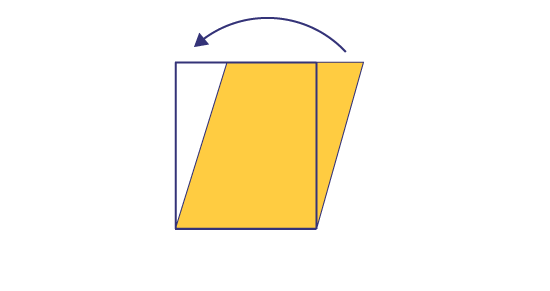
-
Nous avons remarqué que si nous tracions un triangle à droite, à l'intérieur du parallélogramme, que nous le
découpions et le déplacions à gauche, nous obtenions un rectangle dont la base mesure 4 cm et la hauteur mesure
5 cm. Puisque l'aire du rectangle est égale à 20 cm2 (A = b × h),
c'est aussi l'aire du parallélogramme.
Le personnel enseignant amène ensuite les élèves à formuler une généralisation concernant la relation entre les dimensions d'un parallélogramme et son aire, en leur posant des questions telles que :
- Quelle est la mesure de la base du parallélogramme? (La base du parallélogramme mesure 4 cm.)
- Quelle est la mesure de la hauteur du parallélogramme? Comment le savez-vous? (La hauteur du parallélogramme mesure 5 cm. C'est ce que nous obtenons lorsque nous plaçons le parallélogramme verticalement sur la table et lorsque nous mesurons sa hauteur à l'aide d'une règle.)
Note : Plusieurs élèves ont tendance à associer la hauteur du parallélogramme à la mesure de son côté oblique. Elles et ils auront besoin d'examiner différentes situations avant de bien comprendre que la hauteur d'une figure correspond à la distance perpendiculaire entre sa base et son sommet.
image Il y a un parallélogramme. Une ligne pointillée verticale passe au centre du parallélogramme et une ligne pointillée horizontale passe à la base. À côté de la ligne verticale est écrit: hauteur. Sous la ligne horizontale est écrit: base. Le point ou la ligne verticale et horizontale se rencontre est marqué par un carré.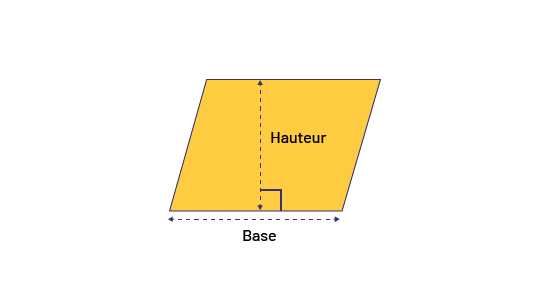
- Quelle relation y a-t-il entre ces deux mesures et l'aire du parallélogramme? (Si nous multiplions ces deux mesures, nous obtenons la mesure de l'aire du parallélogramme.)
- Pensez-vous que cette relation est vraie pour tous les parallélogrammes? Pourquoi? (Oui, parce que la stratégie utilisée pour déterminer l'aire du parallélogramme est la même pour n'importe quel parallélogramme et mène à la même conclusion.)
- Pouvez-vous décrire, en mots et à l'aide de symboles mathématiques, la relation entre les dimensions d'un parallélogramme et son aire? (L'aire d'un parallélogramme est égale au produit de la mesure de sa base et de sa hauteur, soit A = b × h.)
- Comment expliquez-vous que cette relation soit identique à celle d'un rectangle? (Il est possible de transformer un parallélogramme en un rectangle de façon que les deux figures aient la même base et la même hauteur. Ces deux figures ont donc la même aire.)
Note : Le personnel enseignant profite de cette situation pour rappeler aux élèves que tous les rectangles sont
des parallélogrammes.
Le personnel enseignant peut ensuite présenter aux élèves la figure ci-dessous et leur demander :
- Que pouvez-vous dire au sujet de l'aire du parallélogramme vert, de l'aire du parallélogramme orangé et de l'aire du parallélogramme bleu? (Les trois parallélogrammes ont la même aire, puisque les trois ont la même base et la même hauteur.)

Triangle
Lorsque les élèves ont bien compris la façon de déterminer l'aire d'un rectangle et l'aire d'un parallélogramme, ainsi que le sens de la formule A = b × h, elles et ils peuvent utiliser ces connaissances pour établir la relation entre les dimensions d'un triangle et son aire.
Exemple
Le personnel enseignant demande aux élèves de dessiner deux paires de triangles congruents, de les découper et d'assembler chaque paire de façon à former un parallélogramme. Si l'une des paires de triangles est composée de triangles rectangles, le parallélogramme formé sera un rectangle.
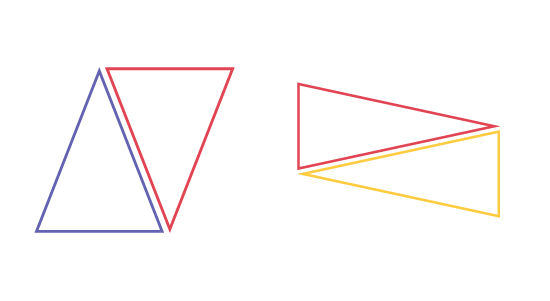
Le personnel enseignant incite ensuite les élèves à établir la relation entre les dimensions du triangle et son aire en leur posant des questions telles que :
- Quelle relation y a-t-il entre la hauteur et la base d'un des triangles, et la hauteur et la base du parallélogramme correspondant? (Le triangle et le parallélogramme correspondant ont la même base et la même hauteur.)
- Comment est-il possible d'utiliser cette relation pour déterminer l'aire d'un triangle? (Nous pouvons d'abord déterminer l'aire du parallélogramme. Ensuite, nous remarquons qu'il faut deux triangles congruents pour former le parallélogramme. Alors, l'aire de chaque triangle doit être égale à la moitié de l'aire du parallélogramme.)
- Pouvez-vous décrire, en mots et à l'aide de symboles mathématiques, la relation entre les dimensions d'un
triangle et son aire? (L'aire du triangle est égale à la moitié du produit de la mesure de sa base et de sa
hauteur, soit \(A = \frac{1}{2}(b \times h)\).)
Dans la vidéo suivante, les élèves calculent l’aire d’un triangle à l’aide du découpage d’un rectangle.
 Description de la vidéo
Description de la vidéo
Description à venir
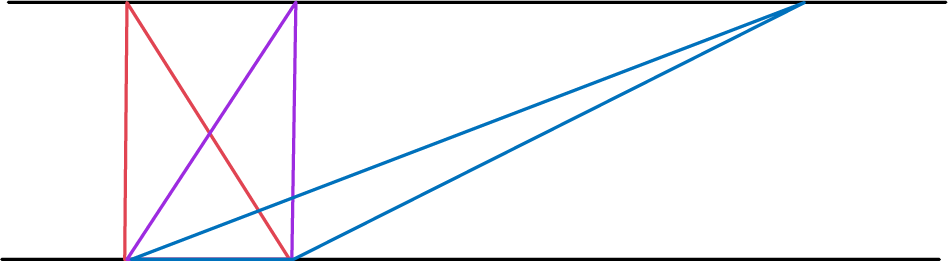
Le personnel enseignant peut ensuite présenter aux élèves la figure ci-dessous et leur demander :
- Que pouvez-vous dire au sujet de l'aire du triangle rouge, de l'aire du triangle violet et de l'aire du triangle bleu? (Les trois triangles ont la même aire, puisque les trois ont la même base et la même hauteur.)
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 70-76.
