At a Glance...

E2.5 Use the area relationships among rectangles, parallelograms, and triangles to develop the formulas for the area of a parallelogram and the area of a triangle, and solve related problems.

Skill: Using the Area Relationships of Rectangles, Parallelograms and Triangles to Develop Formulas for the Area of a Parallelogram and the Area of a Triangle

---

Relationships Between Attributes

Exploring the relationships between attributes allows students to develop a better understanding of the common formulas used to determine the area of certain two-dimensional shape, and to apply them knowledgeably in various problem-solving situations.

Relationship Between Length and Area

Teachers should introduce students to measurement activities that allow them to relate the dimensions (base and height) of certain two-dimensional shapes (rectangle, parallelogram, and triangle) to their area. Students should build the concepts of "height" and "base" through activities that help them understand that any of the sides of a shape can be the base and that for every base there is a corresponding "height".

Rectangle

Students should begin by establishing the relationship between the dimensions of a rectangle and its area. They can then use this relationship to determine the dimensions of the parallelogram and the triangle. When we talk about rectangles, we are also talking about squares, since all squares are part of the set of rectangles.

Example

The teacher gives the students a series of rectangles, as well as the transparency of a grid in square centimetres. The students place the transparency on each rectangle, and determine its base, height and area, recording the results in a table.

During the mathematical conversations, teachers highlight the different strategies that students used to determine the area.

• I placed the transparency on the rectangle and I counted the squares that cover it.
• The area of each rectangle is like an array. I counted the squares in a row and multiplied by the number of rows. In the yellow rectangle, for example, there are 3 rows of 4 squares each. I counted the squares in a column and multiplied by the number of columns. In the red rectangle, for example, there are 2.5 columns of 4 squares each.

The teacher then encourages students to make a generalization about the relationship between the dimensions of a rectangle and its area, first in words (the area of the rectangle is equal to the product of the measurements of its base and its height), then using mathematical symbols (A = b × h).

Parallelogram

Once students understand how to determine the area of a rectangle and the area of a parallelogram, as well as the meaning of the formula A = b × h, they can use this knowledge to establish the relationship between the dimensions of a triangle and its area.

Example

The teacher groups the students into teams of two and gives each team a parallelogram, whose measurement of the base and height correspond to whole numbers (for example, base of 4 cm and height of 5 cm), as well as the transparency of a grid in square centimetres. They then ask the students to find a way to determine the area of the parallelogram.

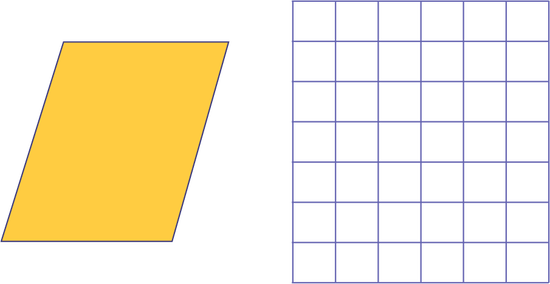
During the mathematical conversations, the teacher highlights the different strategies that students used to determine the area.

Example:

• We placed the transparency on the rectangle and counted the whole squares. Then we noticed that for each row, the part of the square on the left combined with the part of the square on the right resulted in a whole square. We were therefore able to determine that the area of the parallelogram is equal to 20 cm².

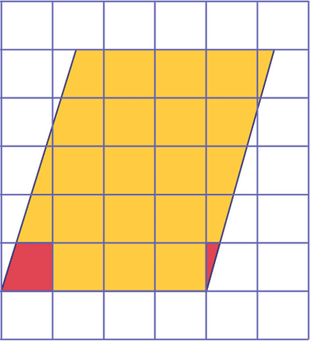
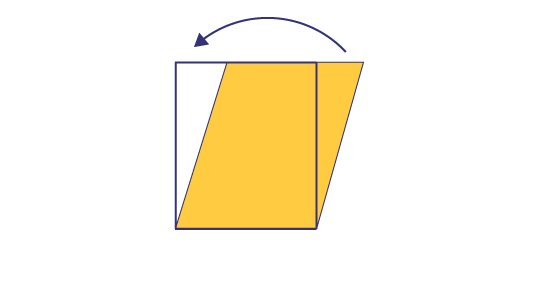
• We noticed that if we drew a triangle on the right, inside the parallelogram, cut it out and moved it to the left, we would get a rectangle with a base of 4 cm and a height of 5 cm. Since the area of the rectangle is equal to 20 cm² (A= b× h), this is also the area of the parallelogram.

The teacher then leads students to formulate a generalization about the relationship between the dimensions of a parallelogram and its area by asking questions such as:

• What is the measurement of the base of the parallelogram? (The base of the parallelogram measures 4 cm.)
• What is the measurement of the height of the parallelogram? (The height of the parallelogram is 5 cm. This is what we get when we place the parallelogram vertically on the table and measure its height with a ruler.)

Note: Many students tend to associate the height of a parallelogram with the measurement of its slanting side, and they will need to examine different situations before they fully understand that the height of a shape is the perpendicular distance between its base and vertex.

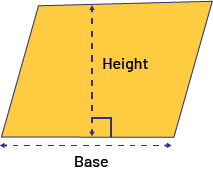image There is a parallelogram. A vertical dotted line passes through the center of the parallelogram and a horizontal dotted line passes through the base. Next to the vertical line is labeled: height. Under the horizontal line is labeled: base. The point where the vertical and horizontal lines meet is marked by a square.

• What is the relationship between these two measurements and the area of the parallelogram? (If we multiply these two measurements, we get the area of the parallelogram.)
• Do you think this relationship is true for all parallelograms? Why? (Yes, because the strategy used to determine the area of the parallelogram is the same for any parallelogram and leads to the same conclusion.)
• Can you describe, in words and using mathematical symbols, the relationship between the dimensions of a parallelogram and its area? (The area of a parallelogram is equal to the product of the measurement of its base and its height, in other words  A = b × h.)
• How do you explain that this relationship is the same as that of a rectangle? (It is possible to transform a parallelogram into a rectangle so that both shapes have the same base and height, so it makes sense that both shapes have the same area.)

Note: The teacher uses this situation to remind students that all rectangles are parallelograms.

The teacher can then show the students the shape below and ask:

• What can you say about the area of the green parallelogram, the area of the orange parallelogram, and the area of the blue parallelogram?(All three parallelograms have the same area, since all three have the same base and height.)

Triangle

Once students understand how to determine the area of a rectangle and the meaning of the common formula (A = b × h), they can use this knowledge to relate the dimensions of a triangle to its area.

Example

The teacher asks students to draw two pairs of congruent triangles, cut them out, and put each pair together to form a parallelogram. If one of the pairs of triangles is made up of right triangles, the parallelogram formed will be a rectangle.

The teacher then prompts students to establish the relationship between the dimensions of the triangle and its area by asking questions such as:

• What is the relationship between the height and base of one of the triangles, and the height and base of the corresponding parallelogram? (The triangle and the corresponding parallelogram have the same base and height.)
• How can we use this relationship to determine the area of a triangle? (First, we can determine the area of the parallelogram. Then, we notice that we need two congruent triangles to form the parallelogram. So, the area of each triangle must be equal to half the area of the parallelogram.)
• Can you describe, in words and using mathematical symbols, the relationship between the dimensions of a triangle and its area?(The area of the triangle is equal to half the product of the measurement of its base and height, in other words, \(A = \frac{1}{2}(b \times h)\).

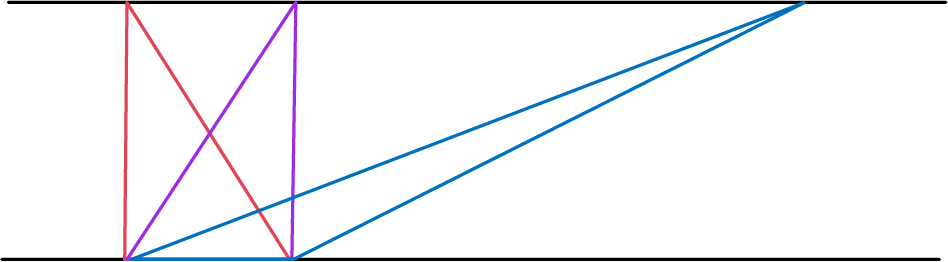
The teacher can then show the students the shape below and ask:

• What can you say about the area of the red triangle, the area of the purple triangle, and the area of the blue triangle? (All three triangles have the same area, since all three have the same base and height.)

Source: translated from Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, Mesure, p. 70-76.