E1. Raisonnement géométrique et spatial
Décrire et représenter la forme, la position et le déplacement en se servant de propriétés géométriques et de relations spatiales pour s’orienter dans le monde qui l’entoure.
SITUATION D'APPRENTISSAGE : UN LOGO DE TRIANGLES!
Durée totale : 90 minutes
Sommaire
Dans cette situation d'apprentissage, les élèves explorent la relation entre la mesure de chacun des côtés d'un triangle en construisant trois triangles différents de même périmètre.
|
Attente |
Contenus |
|
E1. Décrire et représenter la forme, la position et le déplacement en se servant de propriétés géométriques et de relations spatiales pour s’orienter dans le monde qui l’entoure. |
E1.1 reconnaître les propriétés géométriques des triangles et construire divers types de triangles en utilisant des mesures d’angles ou de côtés données. E1.2 reconnaître et construire des triangles, des rectangles et des parallélogrammes congruents. |
Intention pédagogique
Cette situation d'apprentissage a pour but d'amener les élèves :
- à identifier les triangles en fonction de la mesure de chacun de leurs côtés;
- à construire des triangles en tenant compte de restrictions relatives à la mesure de chacun de leurs côtés;
- à développer des stratégies de résolution de problèmes.
|
Contexte |
Préalables |
|
Au cycle primaire, les élèves ont appris à identifier les triangles parmi les figures planes, à les construire et à décrire leurs propriétés relatives au nombre de côtés et de sommets. Selon la théorie des niveaux de pensée en géométrie de Pierre et Dina van Hiele, elles et ils ont progressé du niveau 0, soit visualisation, au niveau 1, soit l'analyse, (voir Fondements généraux). En 5e année, les élèves poursuivent l'étude des triangles. Elles et ils apprennent à les classifier en fonction des mesures des angles et des côtés. |
Dans la présente situation d'apprentissage, les élèves construisent différentes représentations de triangles à l'aide de matériel concret et apprennent à définir ces triangles en fonction des mesures de leurs côtés :
|
Note : Tous les triangles équilatéraux sont aussi des triangles isocèles.
Pour être en mesure de réaliser cette situation d'apprentissage, les élèves doivent comprendre les concepts de périmètre et de congruence de triangles.
Vocabulaire mathématique
figures congruentes, côtés congrus, segment de droite, ligne ouverte, ligne fermée, supérieur à, inférieur à, multiple, périmètre, triangle isocèle, triangle équilatéral, triangle scalène
Matériel
- tableau blanc interactif
- Annexe – Les trois triangles (une copie par équipe)
- grandes feuilles de papier (un par équipe)
- marqueurs (un par équipe)
- bâtonnets à café de même longueur (30 par équipe)
- bâtonnets géo (facultatif)
- logiciel ou application de géométrie dynamique (facultatif)
Avant l'apprentissage (mise en train)
Durée : 15 minutes
Présenter aux élèves la situation suivante :
La direction de l'école souhaite avoir un logo afin de faire la promotion de l'école. Elle aimerait que ce logo représente à la fois les élèves, le personnel de l'école ainsi que les parents, les tutrices et les tuteurs. Elle en a parlé au personnel enseignant lors de la dernière réunion. Au cours des discussions, il a été suggéré que le triangle serait un bon symbole pour représenter chacun des trois groupes qui forment la communauté scolaire. De plus, pour illustrer le fait que chaque groupe tient un rôle différent dans la vie de l'école, il a été recommandé que le logo soit composé de trois triangles différents, mais ayant le même périmètre. Étant donné que nous étudions les triangles cette année, j'ai pensé que le groupe-classe pourrait soumettre certaines suggestions de logos.
Avant de poursuivre l'activité, s'assurer que les élèves comprennent ce qu'est un logo. Au besoin, leur montrer quelques exemples de logos connus et revoir avec elles et eux la définition de périmètre.
Dire aux élèves : « Vous allez d'abord utiliser du matériel concret pour bien visualiser la façon de construire des triangles différents ayant le même périmètre. Vous utiliserez des bâtonnets à café comme unité de mesure. Ainsi, un triangle formé de trois bâtonnets à café, par exemple, aura un périmètre de 3 unités (au besoin, montrer un exemple d'un triangle formé de trois bâtonnets à café). La question est de savoir s'il est possible de former trois triangles différents comportant trois bâtonnets à café chacun. Sinon, est-ce possible avec quatre bâtonnets à café? cinq bâtonnets à café? six bâtonnets à café? Bref, il s'agit de déterminer le nombre de bâtonnets à café qui permet de construire trois triangles différents de même périmètre. Pour des raisons pratiques, vous n'utiliserez pas plus de 10 bâtonnets à café par triangle. »
Au tableau blanc interactif, présenter aux élèves l'Annexe – Les trois triangles. Leur présenter l'énoncé du problème et les critères à respecter dans la construction des trois triangles. Remettre une copie de l'annexe à chaque élève. Leur mentionner également les trois questions ainsi que les éléments à noter en prévision de l'échange mathématique.
Problème
Construire trois triangles différents de même périmètre à l'aide de bâtonnets à café.
Critères
- Les trois triangles doivent être différents, c'est-à-dire non congruents.
- Les trois triangles doivent être construits en utilisant le même nombre de bâtonnets à café (même périmètre).
- Chaque triangle doit être construit en se servant d'au plus 10 bâtonnets à café.
- Les bâtonnets à café ne peuvent pas être superposés ou coupés.
Questions à se poser
- Quel nombre de bâtonnets à café permet de construire trois triangles différents de même périmètre?
- Est-ce le seul nombre possible?
- Y a-t-il une relation entre le nombre de bâtonnets à café de chaque côté du triangle et le fait d'être capable ou pas de construire un triangle?
Communication
- Demander aux élèves de noter leurs essais et leurs observations concernant les combinaisons possibles de bâtonnets à café de chaque côté qui permettent de construire un triangle et les combinaisons qui ne le permettent pas.
- Animer un échange mathématique où les élèves communiquent leurs observations, leurs conclusions et leurs stratégies pour résoudre le problème.
- S'assurer que les élèves ont bien compris le problème à résoudre et les critères à respecter en leur posant
des
questions telles que :
- Qui peut expliquer la tâche à effectuer en ses propres mots?
- Qu'est-ce qu'on entend par des triangles différents?
- Rappeler aux élèves l'importance de noter leurs essais et d'examiner les combinaisons de bâtonnets à café de
chaque côté qui permettent de construire un triangle et les combinaisons qui ne le permettent pas.
Note : En tentant de résoudre le problème, les élèves devraient constater qu'il est impossible de former un
triangle :
- lorsque la somme des mesures de deux côtés est égale à la mesure du troisième, puisqu'une ligne droite est formée (voir l'Exemple 1);
Exemple 1
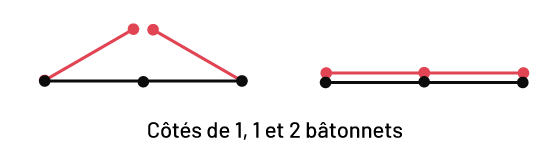image Un segment horizontal de trois bâtonnets. Deux segments de deux
bâtonnets diagonaux vers le haut, chacun partant des extrémités du premier bâtonnet, ne se rejoignent pas tout à
fait au centre. À la droite du premier ensemble de bâtonnets, se trouve un deuxième ensemble. Dans celui-ci, il y a
deux segments de trois bâtonnets horizontaux de longueur égale un par-dessus l’autre. Sous l’image, on peut lire:
côtés de un, un et deux bâtonnets.
- lorsque la somme des mesures de deux côtés est inférieure à la mesure du troisième, puisqu'une ligne ouverte est formée (voir l'Exemple 2).
Exemple 2
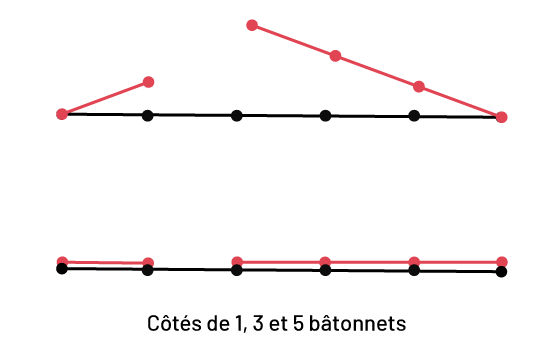image Un segment de six bâtonnets horizontaux. Il y a deux segments de, un
et trois bâtonnets, respectivement, diagonaux vers le haut des extrémités du premier segment. Les deux bâtonnets ne
se rencontrent pas. Sous le premier ensemble de bâtonnets, il y a trois segments horizontaux, ,de, un, trois et cinq
bâtonnets. Sous l’image on peut lire: côtés de un, trois et cinq bâtonnets.
- Les élèves pourraient alors conclure, à l'aide du raisonnement déductif informel (niveau 2 de la pensée en géométrie des van Hiele), qu'il est possible de construire un triangle, si et seulement si, la somme des mesures de deux des côtés est supérieure à la mesure du troisième côté (Exemple 3).
Exemple 3
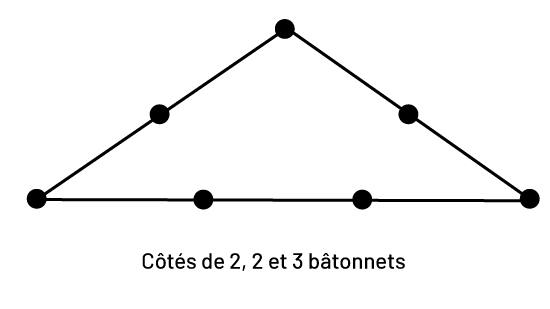
Pendant l'apprentissage (exploration)
Durée : 45 minutes
Grouper les élèves en équipes de deux. Remettre à chaque équipe 30 bâtonnets à café de longueurs égales, une grande feuille et un marqueur.
Allouer suffisamment de temps aux élèves pour leur permettre d'explorer diverses stratégies afin de résoudre le problème. Circuler et observer les stratégies qu'utilise chacune des équipes. Intervenir, au besoin, afin d'aider certaines équipes à cheminer.
|
Observations possibles |
Interventions possibles |
|
Une équipe procède par essais et erreurs et découvre, en dressant une liste partielle, qu'avec 5, 6, 7 ou 8 bâtonnets à café il n'est pas possible de construire trois triangles différents, mais qu'avec 9 bâtonnets à café, c'est possible. |
|
|
Une équipe élimine immédiatement tous les nombres qui ne se divisent pas par 3. Elle commence en utilisant 6 bâtonnets à café, puis passe à 9. |
|
|
Une équipe construit trois triangles congruents, mais dont l'orientation est différente. |
|
|
Une équipe indique qu'en utilisant 8 bâtonnets à café, il est possible de former le triangle 2, 2, 4. |
|
|
Une équipe identifie des situations qui permettent de construire des triangles qui « ferment » et d'autres situations qui permettent de construire des triangles qui « ne ferment pas ». Elle réussit à faire, à l'aide de 4 bâtonnets à café, un triangle qui « ferme un peu ». |
|
Demander aux équipes de noter leurs essais, leurs réflexions et leurs constructions sur les grandes feuilles. Leur demander aussi de préparer leur présentation en utilisant des arguments mathématiques clairs et convaincants ainsi que des termes de causalité (par exemple, puisque, si… alors).
Examiner attentivement les différentes solutions afin de choisir celles qui contribueront le plus à la discussion. Choisir, par exemple, une ou des équipes :
- qui ont fait des observations mettant en évidence certains concepts ou certaines relations (par exemple, pour construire un triangle ayant trois côtés congrus, il faut utiliser 3, 6 ou 9 bâtonnets à café);
- qui ont utilisé différentes stratégies de résolution de problèmes (par exemple, essais et erreurs, liste ordonnée);
- qui ont découvert que certaines combinaisons de bâtonnets à café de chaque côté ne permettent pas de construire un triangle (par exemple, 1, 1, 2 ou 1, 3, 5);
- qui peuvent expliquer la raison pour laquelle neuf est le seul nombre de bâtonnets à café avec lequel il est possible de construire trois triangles différents.
Note : Le tableau ci-dessous présente l'ensemble des triangles possibles en fonction du nombre de bâtonnets à café utilisés. Il est présenté à titre indicatif seulement. Les élèves n'ont pas nécessairement besoin de développer un tableau semblable.
Triangles possibles en fonction du nombre de bâtonnets à café utilisés
| Nombre de bâtonnets | Triangles possibles | ||
|---|---|---|---|
| 1 | Aucun | ||
| 2 | Aucun | ||
| 3 |
1, 1, 1 | ||
| 4 | Aucun | ||
| 5 | 1, 2, 2 | ||
| 6 | 2, 2, 2 | ||
| 7 | 1, 2, 3 | 1, 3, 3 | |
| 8 | 2, 3, 3 | ||
| 9 | 3, 3, 3 | 1, 4, 4 | 2, 3, 4 |
| 10 | 2, 4, 4 | 3, 3, 4 | |
Après l'apprentissage (objectivation et échange mathématique)
Durée : 30 minutes
Demander aux équipes choisies de communiquer leur solution, leur démarche et leurs observations. Profiter de l'occasion pour présenter ou revoir la classification des triangles selon la congruence des côtés (triangles équilatéral, isocèle et scalène).
Voici quelques exemples d'observations possibles formulées à l'aide de termes de causalité :
- Si deux triangles ont une orientation différente, mais qu'ils sont congruents, alors ils ne sont pas différents.
Note : Pour vérifier cette observation, tracer les triangles sur du papier, les découper et les superposer.
- Puisque tous les triangles ont trois côtés, alors il n'est pas possible de construire un triangle en utilisant seulement 1 ou 2 bâtonnets à café.
- Si un triangle a trois côtés congrus, alors, pour le construire, il faut utiliser un multiple de 3 bâtonnets à café.
- Si l'on utilise un maximum de 10 bâtonnets à café par triangle, alors c'est uniquement avec
9 bâtonnets à café qu'il est possible de construire trois triangles différents. Il s'agit des
triangles 2, 3, 4 (trois côtés non congrus), 1, 4, 4 (deux côtés congrus) et 3, 3, 3 (trois côtés congrus).
Note : Cette observation peut servir à présenter ou à revoir la classification des triangles selon la congruence des côtés. - Si la somme des mesures de deux côtés est égale ou inférieure à la mesure du troisième côté, alors il n'est pas possible de construire un triangle.
- Si la somme des mesures de deux côtés est supérieure à la mesure du troisième côté, alors il est possible de construire un triangle.
Exemple d'observation d'une ou d'un élève :
« Nous nous sommes rendu compte que si l'on additionnait un côté à un autre côté, soit le premier côté et le deuxième côté, comme si 1 plus 4 égalent 5, le résultat est toujours plus haut que le troisième côté. »
Inviter les autres élèves à poser des questions ou à résumer ce qu'elles et ils ont compris. Leur demander par exemple :
- Qui peut résumer en ses propres mots l'argument présenté par cette équipe pour expliquer sa solution?
- Est-ce que l'argument présenté était clair et convaincant?
- Qui peut me donner un autre exemple ou un contre-exemple?
- Est-ce toujours vrai?
Représenter la mise en situation et demander à chaque équipe de créer un logo en utilisant les trois différents triangles dont le périmètre est de 9 unités. Cette activité peut être intégrée à la programmation du cours Éducation artistique. Par la suite, demander aux équipes de présenter leur logo au groupe-classe et d'expliquer en quoi il représente bien l'école.
Différenciation pédagogique
|
Pour faciliter la tâche |
Pour enrichir la tâche |
|
|
Note : Le tableau ci-dessous présente l'ensemble des triangles qu'il est possible de construire en utilisant 11 ou 12 bâtonnets à café. On constate qu'avec 11 bâtonnets à café, il est possible de construire quatre triangles différents, dont trois sont isocèles et un est scalène.
Triangles possibles en fonction du nombre de bâtonnets à café utilisés
|
Nombre de bâtonnets |
Triangles possibles |
|||
|
11 |
3, 4, 4 |
1, 5, 5 |
3, 3, 5 |
2, 4, 5 |
|
12 |
3, 4, 5 |
2, 5, 5 |
4, 4, 4 |
|
Suivi à la maison
À la maison, les élèves peuvent :
- trouver des objets de forme triangulaire et en mesurer les côtés afin de vérifier la propriété des triangles relative à la mesure de chaque côté;
- montrer à un membre de sa famille, à l'aide d'exemples et de contre-exemples, que la somme des mesures de n'importe quels deux côtés d'un triangle est toujours supérieure à la mesure du troisième côté.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 53.