E1. Geometric and Spatial Reasoning
Describe and represent shape, location, and movement by applying geometric properties and spatial relationships in order to navigate the world around them.
Learning Situation: A Logo of Triangles!
Total duration: 90 minutes
Summary
In this learning situation, students explore the relationship between the measurement of each side of a triangle by constructing three different triangles of the same perimeter.
|
Overall Expectation |
Specific Expectations |
|
E1. Describe and represent shape, location, and movement by applying geometric properties and spatial relationships in order to navigate the world around them. |
E1.1 Identify geometric properties of triangles, and construct different types of triangles when given side or angle measurements. E1.2 Identify and construct congruent triangles, rectangles, and parallelograms. |
| Learning Goals |
|---|
|
The purpose of this learning situation is to have students:
|
|
Context |
Prerequisites |
|---|---|
|
In the primary grades, students have learned to identify triangles among two-dimensional shapes, to construct them and to describe their properties with respect to the number of sides and vertices. According to Pierre and Dina van Hiele's theory of geometric thinking, they have progressed from Level 0, visualization, to Level 1, analysis (see General Foundations). In Grade 5, students continue their study of triangles. They learn to classify triangles based on angle and side measurements. |
In this learning situation, students construct different representations of triangles using concrete materials and learn to define these triangles based on the measurements of their sides:
Note: All equilateral triangles are also isosceles triangles.
To be able to complete this learning situation, students must understand the concepts of perimeter and congruence of triangles.
|
Mathematical Vocabulary
congruent shapes, congruent sides, line segment, open shape, closed shape, greater than, less than, multiple, perimeter, isosceles triangle, equilateral triangle, scalene triangle
Material
- interactive whiteboard
- Appendix 4.2 (one copy per team)
- large sheets of paper (one per team)
- markers (one per team)
- coffee stir sticks of the same length (30 per team)
- Geostix (optional)
- dynamic geometry software or application (optional)
Before Learning (Warm-Up)
Duration: approximately 15 minutes
Present students with the following situation:
The school administration would like to have a logo to promote the school. They would like this logo to represent the students, the school staff and the parents and guardians. They spoke to the school staff about this at the last meeting. During the discussions, it was suggested that the triangle would be a good symbol to represent each of the three groups that make up the school community. In addition, to illustrate that each group has a different role in the life of the school, it was recommended that the logo be composed of three different triangles, but with the same perimeter. Since we are studying triangles this year, I thought the class group could submit some logo suggestions.
Before continuing the activity, make sure students understand what a logo is. If necessary, show them some examples of known logos and review the definition of perimeter with them.
Tell students, "You will first use concrete materials to visualize how to construct different triangles with the same perimeter. You will use coffee sticks as a unit of measurement. For example, a triangle made of three coffee sticks will have a perimeter of 3 units (if necessary, show an example of a triangle made of three coffee sticks). The question is whether it is possible to form three different triangles with three coffee stir sticks each. If not, is it possible with four coffee stir sticks? five coffee stir sticks? six coffee stir sticks? In short, the question is how many coffee stir sticks are needed to construct three different triangles with the same perimeter. For practical purposes, you will use no more than 10 coffee stir sticks per triangle."
On the interactive whiteboard, introduce students to the Appendix - The Three Triangles. Present the problem and the criteria for constructing the three triangles. Give each student a copy of the Appendix. Also refer to the three questions and the items to be recorded in preparation for the consolidation of learning.
Problem
Construct three different triangles of the same perimeter using coffee stir sticks.
Criteria
- The three triangles must not be congruent.
- The three triangles must be constructed using the same number of stir sticks (same perimeter).
- Each triangle must be constructed using no more than 10 coffee stir sticks.
- Stir sticks cannot be stacked or cut.
Questions to Ask
- What number of stir sticks can be used to construct three different triangles having the same perimeter?
- Is this the only possible number?
- Is there a relationship between the number of coffee stir sticks on each side of the triangle and whether or not you are able to construct a triangle?
Communication
Ask students to record their trials and observations of stir sticks combinations, indicating which can construct a triangle and which cannot.
Facilitate a mathematical conversation during which students share their observations, conclusions, and strategies for solving the problem.
Ensure that students understand the problem to be solved and the criteria to be met by asking questions such as:
- Who would like to explain the task in their own words?
- What do we mean by different triangles?
Remind students of the importance of recording their trials and which combinations of coffee sticks can be used to construct build a triangle and which cannot.
Note: In attempting to solve the problem, students should see that it is impossible to construct a triangle:
- when the sum of the measurements of two sides is equal to the measurement of the third, since a straight line is formed (see Example 1);
Example 1
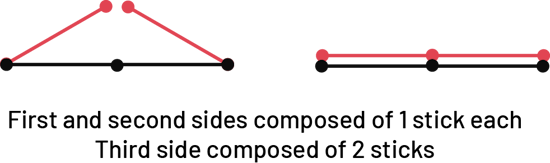image A horizontal segment of three sticks. Two segments of two sticks diagonally upward, each starting from the ends of the first stick, do not quite meet in the center. To the right of the first set of sticks is a second set. In this one, there are two segments of three horizontal sticks of equal length one on top of the other. Under the image is written: sides of one, one and two sticks
- when the sum of the measurements of two sides is less than the measurement of the third because the shape cannot be closed (see Example 2).
Example 2
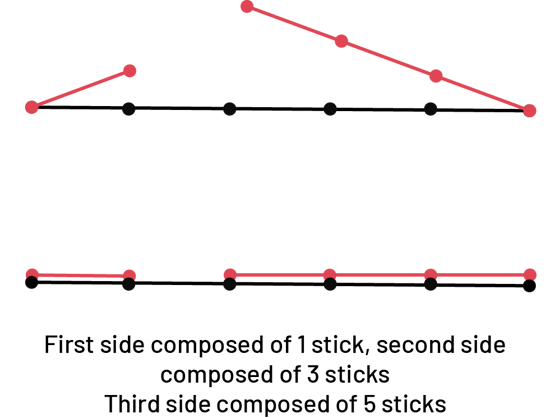image A segment of six horizontal rods. There are two segments of, one and three sticks, respectively, diagonal up from the ends of the first segment. The two sticks do not meet. Under the first set of sticks, there are three horizontal segments, of one, three and five sticks. Under the image is written: sides of one, three and five sticks
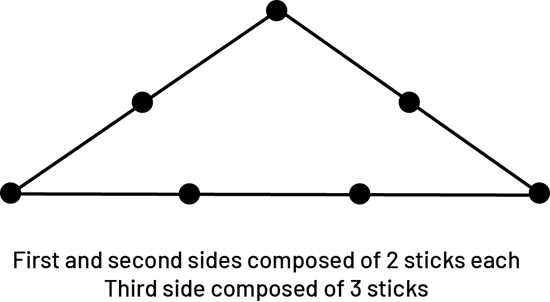
- Students could then conclude, using informal deductive reasoning (Level 2 of van Hiele's Geometric Thinking), that it is possible to construct a triangle, if and only if, the sum of the measurements of two of the sides is greater than the measurement of the third side (Example 3).
Example 3
Active Learning (Exploration)
Duration: approximately 45 minutes
Group students into teams of two. Give each team 30 coffee stir sticks of equal length, a large sheet of paper and a marker.
Allow sufficient time for students to explore various strategies to solve the problem. Circulate and observe the strategies used by each team. Provide support, as necessary to keep all teams moving forward with the task.
|
Possible Observations |
Possible Interventions |
|
A team proceeds by trial and error and discovers, by making a partial list, that with 5, 6, 7 or 8 coffee stir sticks it is not possible to construct three different triangles, but with 9 coffee stir sticks it is possible. |
|
|
One team immediately eliminates all numbers that do not divide by 3. They start with 6 coffee sticks, then move to 9. |
|
|
A team constructs three congruent triangles, but with different orientations. |
|
|
One team reports that using 8 coffee sticks, it is possible to construct the 2, 2, 4 triangle. |
|
|
A team identifies situations that allow them to construct triangles that "close" and other situations that allow them to construct triangles that "don't close". They succeed in making, with the help of 4 stir sticks, a triangle that "closes a little". |
|
Ask teams to record their attempts, reflections and constructions on the large sheets of paper and to prepare their presentation using clear and convincing mathematical arguments and causal terms (for example, since, if… then).
Carefully consider the different solutions to select those that will contribute most to the discussion. Choose, for example, a team or teams:
- who have made observations that highlight certain concepts or relationships (for example, to construct a triangle with three congruent sides, 3, 6, or 9 stir sticks must be used);
- who used different problem-solving strategies (for example, trial and error, ordered list);
- who discovered that certain combinations of stir sticks will not construct a triangle (for example, 1, 1, 2 or 1, 3, 5);
- who can explain why nine is the only number of stir sticks with which it is possible to construct three different triangles.
Note: The table below shows all the possible triangles depending on the number of coffee sticks used. It is presented as a guide only. Students do not necessarily need to develop a similar chart.
Possible Triangles Depending on the Number of Stir Sticks Used
| Number of Sticks | Possible Triangles | ||
|---|---|---|---|
| 1 | None | ||
| 2 | None | ||
| 3 | 1, 1, 1 | ||
| 4 | None | ||
| 5 | 1, 2, 2 | ||
| 6 | 2, 2, 2 | ||
| 7 | 1, 2, 3 | 1, 3, 3 | |
| 8 | 2, 3, 3 | ||
| 9 | 3, 3, 3 | 1, 4, 4 | 2, 3, 4 |
| 10 | 2, 4, 4 | 3, 3, 4 | |
Consolidation of Learning
Duration: approximately 30 minutes
Ask the selected teams to share their solution, approach and observations. Take the opportunity to present or review the classification of triangles according to the congruence of the sides (equilateral, isosceles and scalene triangles).
Examples of possible observations using causal terms include:
- If two triangles have different orientations, but are congruent, then they are not different.
Note: To verify this observation, trace the triangles on paper, cut them out and place them on top of each other.
- Since all triangles have three sides, then it is not possible to construct a triangle using only 1 or 2 coffee stir sticks.
- If a triangle has three congruent sides, then you must use a multiple of 3 coffee stir sticks to construct it.
- If we use a maximum of 10 coffee stir sticks per triangle, then only with 9 coffee stir sticks it is possible to construct three different triangles. These are the triangles 2, 3, 4 (three non-congruent sides), 1, 4, 4 (two congruent sides) and 3, 3, 3 (three congruent sides).
Note: This observation can be used to introduce or review the classification of triangles by side congruence. - If the sum of the measurements of two sides is equal to or less than the measurement of the third side, then it is not possible to construct a triangle.
- If the sum of the measurements of two sides is greater than the measurement of the third side, then it is possible to construct a triangle.
Example of a Student Observation:
"We realized that if you added one side to another side, which is the first side and the second side, like if 1 plus 4 equals 5, the result is always higher than the third side."
Invite other students to ask questions or summarize what they have understood. For example, ask them:
- Who can summarize in their own words the argument presented by this team to explain their solution?
- Was the argument presented clear and convincing?
- Who can give me another example or counterexample?
- Is this still true?
Show the scenario and ask each team to create a logo using the three different triangles with a perimeter of 9 units. This activity can be integrated into an Art class. Afterwards, ask the teams to present their logo to the class and explain how it represents the school.
Differentiated Instruction
|
To Facilitate the Task |
To Enrich the Task |
|
|
Note: The table below shows the set of triangles that can be constructed using 11 or 12 coffee sticks. We can see that with 11 coffee stir sticks, it is possible to construct four different triangles, three of which are isosceles and one is scalene.
Possible Triangles Depending on the Number of Stir Sticks Used
|
Number of Sticks |
Possible Triangles |
|||
|
11 |
3, 4, 4 |
1, 5, 5 |
3, 3, 5 |
2, 4, 5 |
|
12 |
3, 4, 5 |
2, 5, 5 |
4, 4, 4 |
|
Follow-up at Home
At home, students can:
- look for triangle-shaped objects and measure their sides to verify the property of triangles relating to length of each side;
- show a family member, using examples and counterexamples, that the sum of the measurements of any two sides of a triangle is always greater than the measurement of the third side.