E2.6 Déterminer l’aire totale de prismes et de pyramides en calculant les aires de chaque face et en les additionnant.
ACTIVITÉ 1 : EXPLORER L’AIRE TOTALE
Demander aux élèves d’explorer ces questions en équipes de deux.
- Déterminer l’aire de ce prisme.
- Quel est le nombre minimal d’aires que tu dois déterminer séparément pour être en mesure de déterminer l’aire du prisme? Pourquoi?
Source : Réduction des écarts de rendement, 9e année, p. 21-22.
ACTIVITÉ 2 : VRAI OU FAUX
Afficher les trois énoncés ci-dessous sur des murs de la salle de classe ou dans le corridor.
Demander aux élèves de se rendre, avec une ou un partenaire, aux trois énoncés et de discuter de leurs réponses (vrai ou faux).
Animer un échange mathématique afin que les élèves défendent leur choix.
Situation
Dans une situation où l’on cherche à déterminer l’aire d’un prisme dont la base est un quadrilatère, indique si les énoncés sont vrais ou faux. Explique tes réponses.
A : Toutes les faces peuvent avoir la même aire.
B : Au moins deux faces ont nécessairement la même aire.
C : Il est possible d’avoir exactement quatre faces avec la même aire.
Source : Réduction des écarts de rendement, 9e année, p. 22.
ACTIVITÉ 3 : POSSIBLE OU IMPOSSIBLE
Est-il possible qu’un prisme d’une certaine hauteur ait une aire plus petite qu’un prisme moins haut?
Explique ta réponse.
Source : Réduction des écarts de rendement, 9e année, p. 23.
ACTIVITÉ 4 : MESURER L’AIRE TOTALE DE PRISMES ET DE PYRAMIDES À PARTIR DES DÉVELOPPEMENTS – PRATIQUE GUIDÉE
Exemple 1
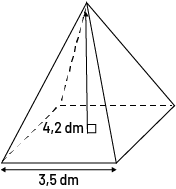
a) Crée le développement de cette pyramide à base carrée et utilise-le pour déterminer l’aire totale du solide.
Image
Pyramide à base carrée, une flèche qui part du sommet d’une des faces triangulaires. À côté de la flèche est écrit:
quatre virgule deux décimètres. Il y a une autre flèche le long de la base. Sous la flèche est écrit trois virgule
cinq décimètres.
b) Crée le développement de ce prisme et utilise-le pour déterminer l’aire totale du solide.
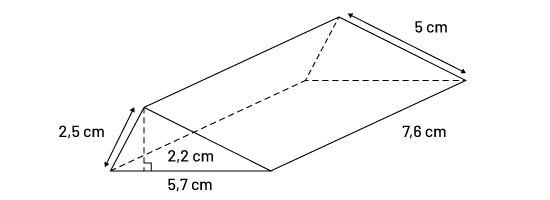Image Il
y a un prisme dont trois faces triangulaires et deux bases triangulaires sont visibles. À côté d’une flèche le long
d’un des côtés de la base est écrit: cinq centimètres. À côté d’une flèche le long du côté le plus court de la base
est écrit deux virgule cinq centimètre. Sous le dernier côté du triangle est écrit: cinq virgule sept centimètres.
Dans le triangle, il y une ligne pointillée qui va d’un sommet à la base. Le long de cette ligne est écrit: deux
virgules deux centimètres. Sur le côté le plus long d’une des faces est écrit: sept virgule six centimètres.
Exemple 2
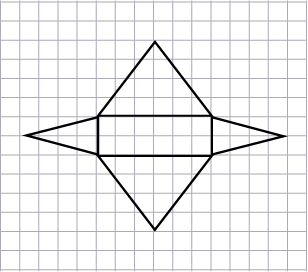
a) Voici le développement d’un prisme. Utilise le développement pour déterminer l’aire totale du solide en sachant qu’un carré représente 1 cm2.
b) Voici le développement d’une pyramide. Utilise ce développement pour déterminer l’aire totale de ce solide en sachant qu’un carré représente 1 cm2.
Source : En avant, les maths!, 6e année, ML, Sens de l’espace, p. 4-10.