E2.6 Determine the surface areas of prisms and pyramids by calculating the areas of their two-dimensional faces and adding them together.
Activity 1: Exploring the Surface Area
Have students explore these questions in pairs.
- Determine the area of this prism.
Image There is a prism, of which two rectangular faces and one square base are visible. On the longest side is written: ten centimeters. On the shortest side is written: five centimeters.
- What is the minimum number of areas you must determine separately to be able to determine the surface area of the prism? Why?
Source: translated from Réduction des écarts de rendement, 9e année, p. 21-22.
Activity 2: True or False
Post the three statements below on classroom walls or in the hallway.
Ask students to go with a partner to the three statements and discuss their answers (true or false).
Facilitate a mathematical conversation so that students justify their choices.
Situation
In a situation where you are trying to determine the surface area of a prism whose base is a quadrilateral, indicate whether the statements are true or false. Explain your answers.
A: All faces can have the same area.
B: At least two faces must have the same area.
C: It is possible to have exactly four faces having the same area.
Source: translated from Réduction des écarts de rendement, 9e année, p. 22.
Activity 3: Possible or Impossible
Is it possible for a prism of a certain height to have a smaller area than a prism of lesser height?
Explain your answer.
Source: translated from Réduction des écarts de rendement, 9e année, p. 23.
Activity 4: Measuring the Surface Area of Prisms and Pyramids from the Nets - Guided Practice
Example 1
a) Create the net of this square-based pyramid and use it to determine its surface area.
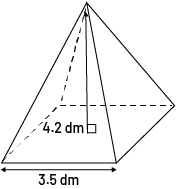Image pyramid with a square base, an arrow starts from the base of one of the triangular bases. Next to the arrow is written: four comma two decimeters. There is another arrow along the base. Below the arrow is written three coma five decimeters.
b) Create the net of this prism and use it to determine its surface area.
Image there is a prism with three triangular faces and two triangular bases, all of which are visible. Next to one of the arrows along of the side of the base is written: five centimeters. Next to the shortest sides is written: two comma five centimeters. Below the last corner of the triangle is written: five comma seven centimeters. In the triangle, there is a dotted line that goes from the base on the basis. Along this line is written: two comma two centimeters. On the longest side of one of the faces is written seven comma six centimeters.
Example 2
a) Here is the net of a prism. Use the net to determine its surface area where one square has an area of 1 cm2.
b) Here is the net of a pyramid. Use this net to determine its surface area where one square has an area of 1 cm2.
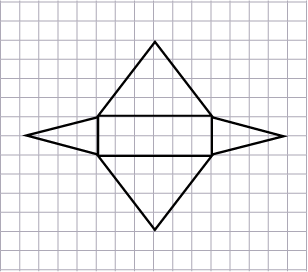
Source: translated from En avant, les maths!, 6e année, ML, Sens de l’espace, p. 4-10.