E1.1 Créer des listes des propriétés géométriques de divers types de quadrilatères, y compris les propriétés des diagonales, la symétrie rotationnelle et les axes de symétrie.
HABILETÉ : CRÉER DES LISTES DES PROPRIÉTÉS GÉOMÉTRIQUES DES DIAGONALES DES QUADRILATÈRES
Les activités de classement et de comparaison de différents quadrilatères sont très importantes pour développer la compréhension des nombreuses propriétés qu’ils possèdent. Au départ, inviter les élèves à comparer deux ou trois quadrilatères et à justifier leurs réponses. Au fil du temps, les élèves seront à l’aise d’utiliser le vocabulaire des propriétés et de classer les diagonales des quadrilatères à l’aide de listes.
Trapèze

Deux diagonales
Parallélogramme

Deux diagonales qui se coupent en leur milieu.
Cerf-volant

Deux diagonales perpendiculaires
Losange
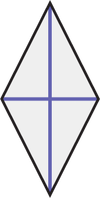
Deux diagonales congrues qui se coupent en leur milieu.
Rectangle

Deux diagonales qui se coupent en leur milieu.
Carré

Deux diagonales congrues et perpendiculaires qui se coupent en leur milieu.
Deltoïde
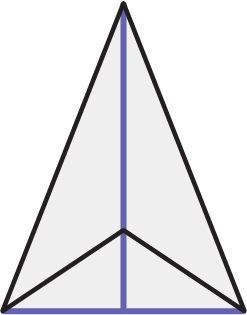
Deux diagonales perpendiculaires dont l’une est à l’extérieur de la figure.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 35-36.
HABILETÉ : CRÉER DES LISTES DES PROPRIÉTÉS GÉOMÉTRIQUES DE LA SYMÉTRIE ROTATIONNELLE DES QUADRILATÈRES
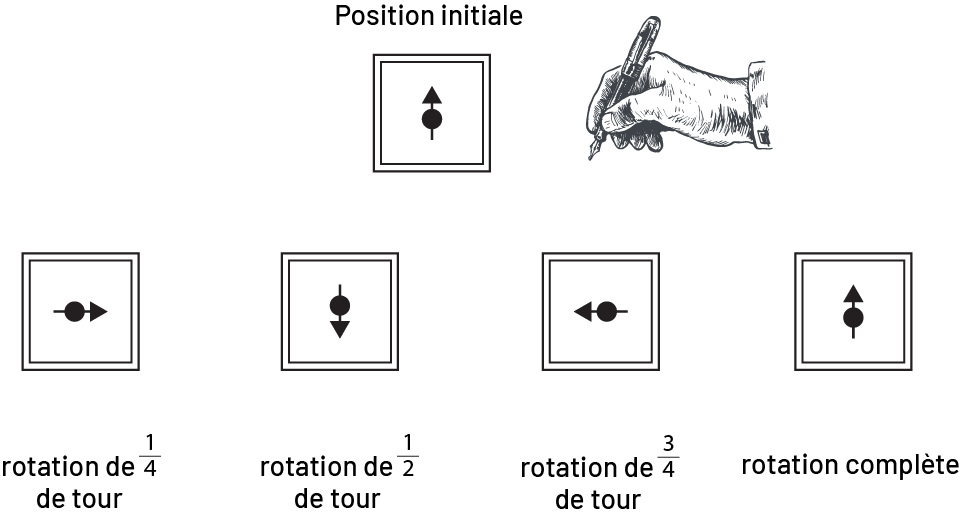 Image Figure un : Deux rectangles dont l’un est plus petit que l’autre, il est inséré dans le premier.
Au centre de
ce rectangle, il y a une flèche de rotation. Figure 2 : Le petit carré a fait une rotation d’un quart de tour vers la
droite. Figure 3 : Le petit carré a fait une rotation d’un demi-tour. Figure 4 : Le petit carré a fait une rotation de
trois quarts. Figure 5 : Le petit carré a fait une rotation complète, et est revenu au point initial.
Image Figure un : Deux rectangles dont l’un est plus petit que l’autre, il est inséré dans le premier.
Au centre de
ce rectangle, il y a une flèche de rotation. Figure 2 : Le petit carré a fait une rotation d’un quart de tour vers la
droite. Figure 3 : Le petit carré a fait une rotation d’un demi-tour. Figure 4 : Le petit carré a fait une rotation de
trois quarts. Figure 5 : Le petit carré a fait une rotation complète, et est revenu au point initial.
Lorsqu’on fait tourner un carré autour de son centre, sa position correspond à sa position initiale après une rotation de \(\frac{1}{4}\), de \(\frac{1}{2}\) et de \(\frac{3}{4}\) de tour: le carré présente donc une symétrie de rotation. Il possède une symétrie de rotation d’ordre 4, car sa position correspond à la position initiale quatre fois au cours d’une rotation complète. Une recherche importante consiste à explorer la relation entre le nombre de côtés du polygone et son ordre de symétrie de rotation. Tous les polygones réguliers ont un ordre de symétrie égal à leur nombre de côtés – un carré a un ordre de symétrie de 4, un hexagone régulier a un ordre de symétrie de rotation de 6, et ainsi de suite. Les élèves du cycle moyen peuvent déterminer la symétrie de rotation et l’ordre de symétrie de rotation de formes bidimensionnelles en traçant une forme, puis en la faisant tourner à l’intérieur du tracé pour déterminer si elle s’adaptera à plus d’un sens.
Le personnel enseignant devrait donner aux élèves l’occasion de déterminer la symétrie de rotation dans une variété de formes bidimensionnelles et leur demander de créer leurs propres formes bidimensionnelles en tenant compte de l’ordre de symétrie de rotation. Au fil du temps, les élèves seront à l’aise d’utiliser le vocabulaire des propriétés et de classer les axes de symétrie rotationnelle des quadrilatères à l’aide de listes.
Source : A Guide to Effective Instruction in Mathematics, Kindergarten to Grade 6, p. 47-48.
HABILETÉ : CRÉER DES LISTES DES PROPRIÉTÉS GÉOMÉTRIQUES DES AXES DE SYMÉTRIE DES QUADRILATÈRES
Des activités de classement et de comparaison de différents quadrilatères sont très importantes pour développer la compréhension des nombreuses propriétés qu’ils possèdent. Au départ, inviter les élèves à comparer deux ou trois quadrilatères et à justifier leurs réponses. Au fil du temps, les élèves seront à l’aise d’utiliser le vocabulaire des propriétés et de classer les axes de symétrie des quadrilatères à l’aide de listes.
Trapèze

Peut avoir un axe de symétrie. Pas dans ce cas.
Parallélogramme

Aucun axe de symétrie
Cerf-volant

Un axe de symétrie
Losange
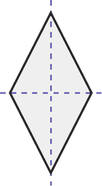
Deux axes de symétrie
Rectangle
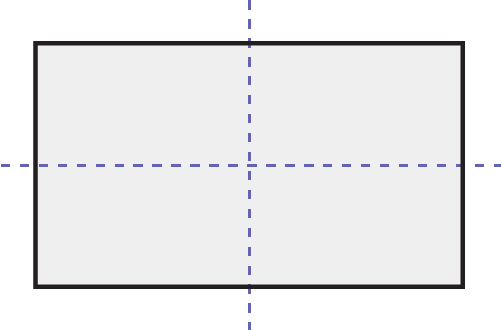
Deux axes de symétrie
Carré
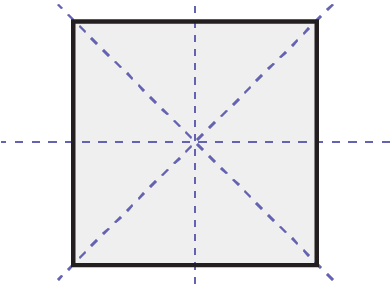
Quatre axes de symétrie
Deltoïde
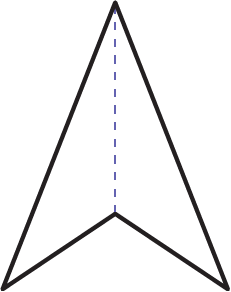
Un axe de symétrie
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 35-36.
Les élèves croient souvent qu’une diagonale d’un parallélogramme est un axe de symétrie. Cela est vrai pour les losanges et les carrés, mais pas pour les autres parallélogrammes. Cette erreur courante vient du fait que les deux triangles de part et d’autre de la diagonale sont congruents.
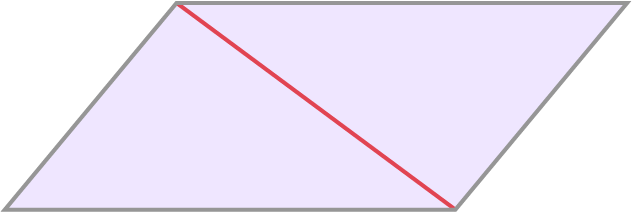
La comparaison des différents types de parallélogrammes permet aux élèves de voir :
- que les losanges et les carrés ont des côtés congrus qui permettent la formation de deux axes de symétrie;
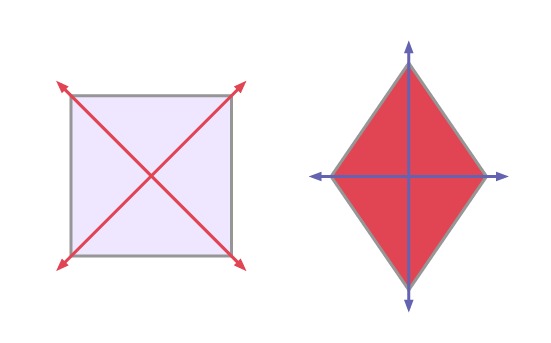
- que les rectangles et les carrés ont des angles de 90º qui permettent la formation de deux axes de symétrie;
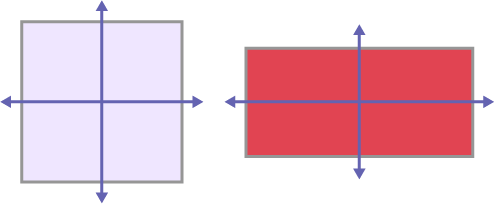
- qu’il est impossible de plier un parallélogramme pour que les deux parties soient identiques.
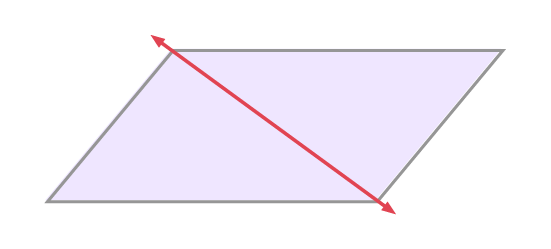
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 38-39.
CONNAISSANCE : PROPRIÉTÉ GÉOMÉTRIQUE
Une propriété est une caractéristique particulière qui sert à définir une forme géométrique ou une famille de formes géométriques, c’est-à-dire le nombre de côtés, la mesure des angles, le nombre de diagonales. Attention à ne pas confondre les propriétés avec les attributs. Les attributs décrivent l’apparence physique d’une forme, par exemple, sa taille, sa couleur et sa texture.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 5.
Au cycle primaire, les élèves apprennent à décrire les formes géométriques en fonction d’une liste de propriétés nécessaires (par exemple, un rectangle est une figure plane qui a quatre côtés, quatre angles droits et des côtés opposés qui sont congrus et parallèles).
Propriétés nécessaires : Les propriétés nécessaires d’une forme géométrique constituent l’ensemble des propriétés que possède cette forme. Au cycle moyen, la pensée géométrique des élèves progresse vers le niveau 2 au fur et à mesure que leur capacité d’abstraction se développe. Cette capacité est liée à la faculté de concentrer son attention sur certaines propriétés de façon isolée. Elle leur permet entre autres de choisir, parmi la liste de propriétés nécessaires d’une forme géométrique, celles qui suffisent à la définir (propriétés suffisantes). Par exemple, un rectangle est une figure plane qui a quatre angles droits et deux paires de côtés congrus. Propriétés suffisantes : Les propriétés suffisantes d’une forme géométrique constituent une liste minimale de propriétés qui suffisent à définir la forme. Cette liste forme donc un sous-ensemble de l’ensemble des propriétés nécessaires.
Source : adapté Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 32-33.
CONNAISSANCE : TYPES DE QUADRILATÈRES
Un quadrilatère est un polygone qui possède quatre côtés, quatre angles et au moins deux diagonales. La somme intérieure des angles est 360°.
Les quadrilatères forment une classe complexe de polygones. Les rectangles étant les plus connus et vus dans le quotidien, il importe de présenter les familles de quadrilatères en utilisant des critères d’inclusion et d’exclusion. Il y a différentes écoles de pensée pour décrire et classer les quadrilatères selon leurs propriétés. Par exemple, certains mathématiciens et mathématiciennes considèrent un parallélogramme comme étant un trapèze, puisqu’il a au moins une paire de côtés parallèles; d’autres préfèrent que les trapèzes soient dans une classe à part.
Voici les différents types de quadrilatères :
Trapèze
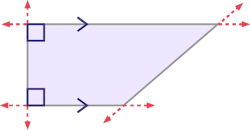
Parallélogramme
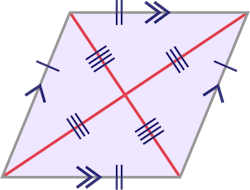
Cerf-volant
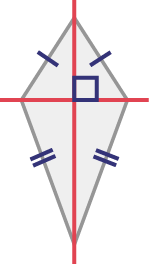
Losange
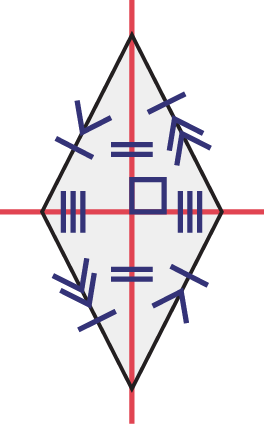
Rectangle
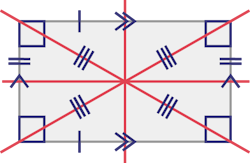 Image Un quadrilatère ayant deux
ensembles de ligne parallèles égales. Une ligne verticale et une ligne horizontale se croisent au centre de la forme
et deux lignes obliques se croisent au centre de la figure.
Image Un quadrilatère ayant deux
ensembles de ligne parallèles égales. Une ligne verticale et une ligne horizontale se croisent au centre de la forme
et deux lignes obliques se croisent au centre de la figure.
Carré
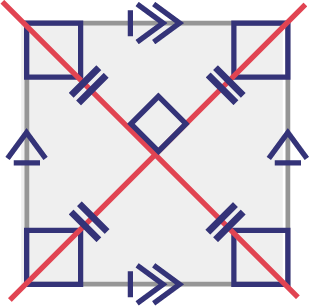
Deltoïde
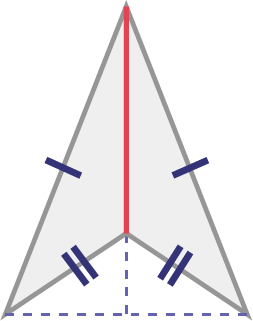
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 34-36.
CONNAISSANCE : DIAGONALE
Tout segment reliant deux sommets non consécutifs (non reliés par un côté).
• Deux diagonales congrues
• Deux diagonales perpendiculaires
• Deux diagonales qui se coupent en leur milieu.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 28.
Exemple
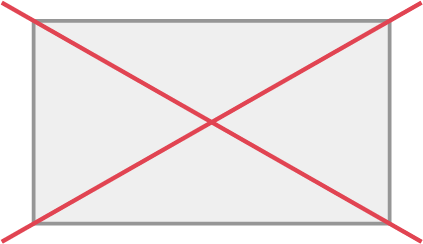
CONNAISSANCE : SYMÉTRIE ROTATIONNELLE
Il y a symétrie rotationnelle lorsque la position d’une forme correspond à sa position d’origine après que la forme a
été tournée de moins de 360°. L’ordre de symétrie rotationnelle se réfère au nombre de fois que la position d’une
forme correspond à sa position originale pendant une rotation complète autour de son centre.
Exemples
Carré
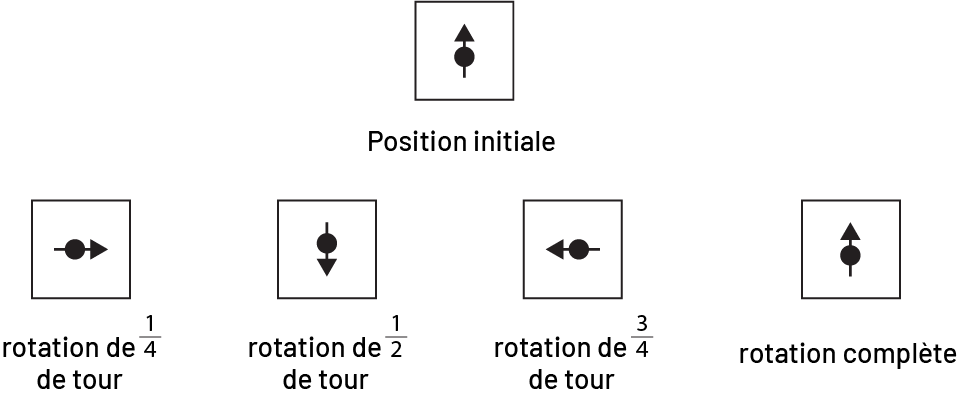 Image Une série, de cinq carrés, ayant un
point de rotation au centre. Sous le premier carré est écrit: position initiale. Sous le deuxième carré est écrit:
rotation d’un quart de tour. Sous le troisième carré est écrit: rotation d’un demi-tour. Sous le quatrième carré est
écrit: rotation de trois quart de tour. Sous le cinquième carré est écrit: rotation complète.
Image Une série, de cinq carrés, ayant un
point de rotation au centre. Sous le premier carré est écrit: position initiale. Sous le deuxième carré est écrit:
rotation d’un quart de tour. Sous le troisième carré est écrit: rotation d’un demi-tour. Sous le quatrième carré est
écrit: rotation de trois quart de tour. Sous le cinquième carré est écrit: rotation complète.
Le carré présente une symétrie de rotation de l’ordre de 4.
Source : A Guide to Effective Instruction in Mathematics, Kindergarten to Grade 6, p. 47.
Losange
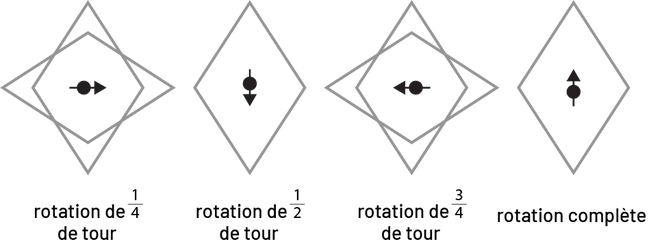 Image Quatre ensembles de losanges sont
présentés. Le premier est un losange horizontal superposé à un losange vertical. Au centre, il y a une flèche qui
pointe à droite. En dessous il est écrit : rotation d’un quart de tour. Le deuxième est un losange vertical, avec une
flèche au centre qui pointe vers le bas. En dessous, il est écrit : rotation d’un demi-tour. Le troisième est un
losange horizontal superposé à un losange vertical. La flèche au centre pointe à gauche. En dessous, il est écrit :
rotation de trois quarts de tour. Le quatrième est un losange vertical avec la flèche au centre qui pointe en haut. En
dessous, il est écrit : rotation complète.
Image Quatre ensembles de losanges sont
présentés. Le premier est un losange horizontal superposé à un losange vertical. Au centre, il y a une flèche qui
pointe à droite. En dessous il est écrit : rotation d’un quart de tour. Le deuxième est un losange vertical, avec une
flèche au centre qui pointe vers le bas. En dessous, il est écrit : rotation d’un demi-tour. Le troisième est un
losange horizontal superposé à un losange vertical. La flèche au centre pointe à gauche. En dessous, il est écrit :
rotation de trois quarts de tour. Le quatrième est un losange vertical avec la flèche au centre qui pointe en haut. En
dessous, il est écrit : rotation complète.
Le losange présente une symétrie de rotation de l’ordre de 2 (au moins).
Rectangle
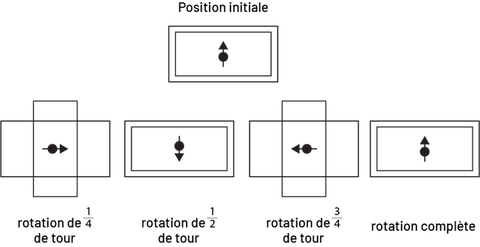 Image Quatre ensembles de rectangles sont
présentés. Le premier est un rectangle horizontal superposé à un rectangle vertical. Au centre, il y a une flèche qui
pointe à droite. En dessous il est écrit : rotation d’un quart de tour. Le deuxième est un rectangle horizontal, avec
une flèche au centre qui pointe vers le bas. En dessous, il est écrit : rotation d’un demi-tour. Le troisième est un
rectangle horizontal superposé à un rectangle vertical. La flèche au centre pointe à gauche. En dessous, il est écrit
: rotation de trois quarts de tour. Le quatrième est un rectangle horizontal avec la flèche au centre qui pointe en
haut. En dessous, il est écrit : rotation complète.
Image Quatre ensembles de rectangles sont
présentés. Le premier est un rectangle horizontal superposé à un rectangle vertical. Au centre, il y a une flèche qui
pointe à droite. En dessous il est écrit : rotation d’un quart de tour. Le deuxième est un rectangle horizontal, avec
une flèche au centre qui pointe vers le bas. En dessous, il est écrit : rotation d’un demi-tour. Le troisième est un
rectangle horizontal superposé à un rectangle vertical. La flèche au centre pointe à gauche. En dessous, il est écrit
: rotation de trois quarts de tour. Le quatrième est un rectangle horizontal avec la flèche au centre qui pointe en
haut. En dessous, il est écrit : rotation complète.
Le rectangle présente une symétrie de rotation de l’ordre de 2.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario
CONNAISSANCE : AXE DE SYMÉTRIE
Une figure a une symétrie de réflexion si une moitié de la figure est une réflexion de l’autre moitié par rapport à un axe appelé l’axe de symétrie. Les figures peuvent avoir un ou plusieurs axes de symétrie.
• Un axe de symétrie
• Deux axes de symétrie (ou plus)
• Aucun axe de symétrie
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 28.
Exemple
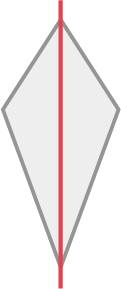
Ce cerf-volant a un axe de symétrie.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 35.
