E1.1 Create lists of the geometric properties of various types of quadrilaterals, including the properties of the diagonals, rotational symmetry, and line symmetry.
Skill: Creating Lists of Geometric Properties of Diagonals of Quadrilaterals
Classifying and comparing different quadrilaterals are very important skills for developing an understanding of their geometric properties, such as diagonals. Initially, invite students to compare two or three quadrilaterals and justify their answers. Over time, students will become comfortable using the vocabulary associated with classifying and comparing the diagonals of quadrilaterals. For example :
Trapezoid
Two diagonals
Parallelogram
Two diagonals that bisect each other.
Kite
Two perpendicular diagonals
Rhombus
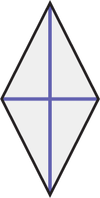
Two perpendicular diagonals that bisect each other.
Rectangle
Two congruent diagonals that bisect each other.
Square
Two congruent and perpendicular diagonals that bisect each other.
Deltoid
Two perpendicular diagonals, one of which is outside the shape.
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Géométrie et sens de l'espace, Document d'appui, Fascicule 1, p. 35-36.
Skill: Creating Lists of Geometric Properties of Rotational Symmetry of Quadrilaterals
Image Figure one: Two rectangles, one of which is smaller than the other, is inserted in the first. At the centre of this rectangle there is a rotating arrow. Figure two: The small square has made a quarter-turn rotation to the right. Figure three: The little square has made a half-turn rotation. Figure four: The little square has made a three-quarter-turn rotation. Figure five: The little square has made a complete rotation and has returned to the starting point.
When a square is rotated about its centre, its position matches its original position after a \(\frac{1}{4}\) rotation, a \(\frac{1}{2}\) rotation, and a \(\frac{3}{4}\) rotation. Therefore, a square has rotational symmetry of order 4 because its position matches the original position four times during a complete rotation. It is important to explore the relationship between the number of sides of the polygon and its order of rotational symmetry. All regular polygons have a rotational symmetry order equal to their number of sides – a square has a rotational symmetry order of 4, a regular hexagon has a rotational symmetry order of 6, and so on. Students in the junior grades can determine the rotational symmetry and order of rotational symmetry of two-dimensional shapes by tracing a shape, then rotating it within the drawing to determine if it will fit in more than one direction.
Teachers should give students the opportunity to determine rotational symmetry in a variety of two-dimensional shapes and have them create their own two-dimensional shapes with the order of rotational symmetry in mind. Over time, students will become comfortable using the vocabulary of properties and classifying the lines of rotational symmetry of quadrilaterals using lists.
Source: A Guide to Effective Instruction in Mathematics, Kindergarten to Grade 6, p. 47-48.
Skill: Creating Lists of Geometric Properties of Lines of Symmetry of Quadrilaterals
Classifying and comparing different quadrilaterals are very important skills for developing an understanding of their geometric properties, such as lines of symmetry. Initially, invite students to compare two or three quadrilaterals and justify their answers. Over time, students will become comfortable using the vocabulary associated with classifying and comparing lines of symmetry.
Trapezoid
May have lines of symmetry; however the illustrated trapezoid does not.
Parallelogram
No line of symmetry
Kite
One line of symmetry
Rhombus
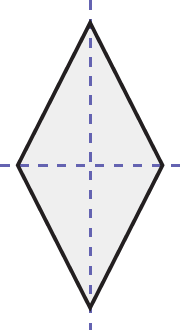A diamond whose sides are all equal. There is a dotted vertical line and a dotted horizontal line which intersect in the centre of the shape.
Two lines of symmetry
Rectangle
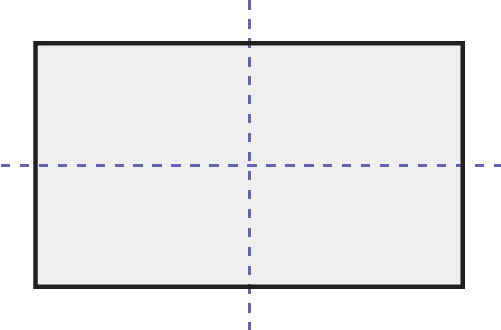Image A rectangle with two sets of equal parallel lines. There is a dotted vertical line and a dotted horizontal line which intersect in the centre of the shape.
Two lines of symmetry
Square
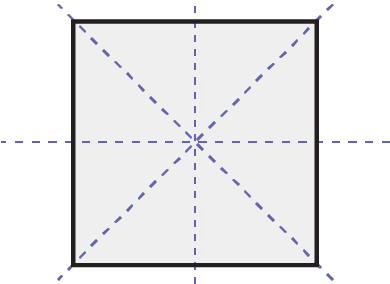Image a square whose sides are all equal. There is a dotted vertical line and a dotted horizontal line which intersect in the centre of the shape.
Four lines of symmetry
Deltoid
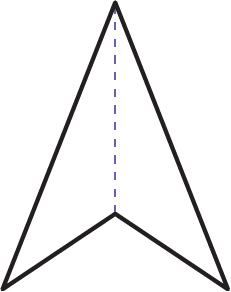Image a deltoid with two sets of equal lines, each forming an angle. There is a dotted vertical line and a dotted horizontal line which intersect in the centre of the shape.
One line of symmetry
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Géométrie et sens de l'espace, Document d'appui, Fascicule 1, p. 35-36.
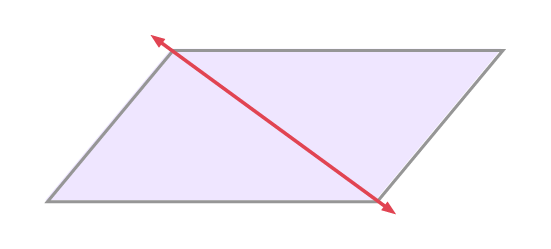
Students often believe that a diagonal of a parallelogram is a line of symmetry. This is true for rhombuses and squares, but not for other parallelograms. This common mistake is because the two triangles on either side of the diagonal are congruent.
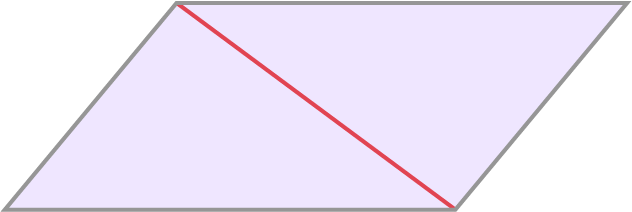
Comparing the different types of parallelograms allows students to see that:
- rhombuses and squares have congruent sides and two lines of symmetry
- rectangles and squares have 90º angles and two lines of symmetry;
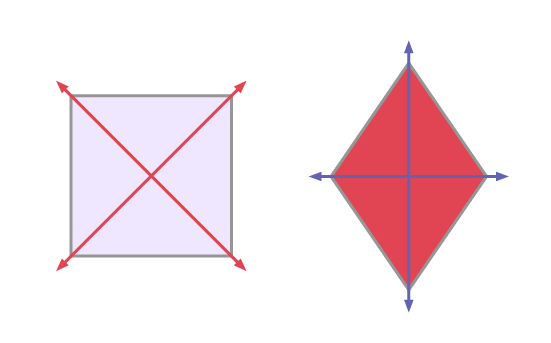Image a square and a diamond. Two oblique lines intersect in the centre of the square. A vertical and a horizontal line intersect in the centre of the diamond.
- rectangles and squares have 90º angles that allow for the generation of two lines of symmetry;
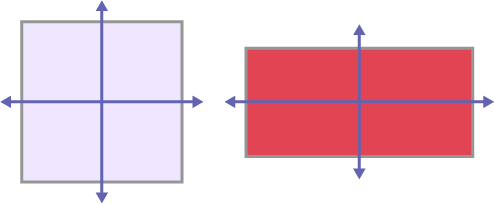Image a square and a rectangle. Two oblique lines intersect in the centre of the square. A vertical and a horizontal line intersect in the centre of the rectangle.
- it is impossible to fold a parallelogram so that the two parts are identical.
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Géométrie et sens de l'espace, Document d'appui, Fascicule 1, p. 38-39.
Knowledge: Geometric Property
A property is a particular characteristic that is used to sort and define a geometric shape or a class of geometric shapes, namely, the number of sides, the measure of angles, the number of diagonals. Be careful not to confuse properties and attributes. Attributes describe the physical appearance of a shape, such as its size, colour, and texture.
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Géométrie et sens de l'espace, Document d'appui, Fascicule 1, p. 5.
In primary grades, students learn to describe geometric shapes based on a list of necessary properties (for example, a rectangle is a two-dimensional shape that has four sides, four right angles, and opposite sides that are congruent and parallel). The necessary properties of a geometric shape constitute the set of properties possessed by this shape. In the junior grades, students' geometric thinking progresses as their ability to think abstractly develops. This ability is related to the ability to focus one's attention on certain properties in isolation. Among other things, it allows them to choose, from the list of necessary properties of a geometric shape, those that are sufficient to define it (sufficient properties). For example, a rectangle is a two-dimensional shape that has four right angles and two pairs of congruent sides. The sufficient properties of a geometric shape constitute a minimum list of properties that are sufficient to define the shape. Therefore, this list forms a subset of the set of necessary properties.
Source: adapted and translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 1, p. 32-33.
Knowledge: Types of Quadrilaterals
A quadrilateral is a polygon with four sides, four angles, and at least two diagonals. The interior angles add up to 360°.
Quadrilaterals are a complex class of polygons. Since rectangles are the most familiar and seen in everyday life, it is important to present families of quadrilaterals using inclusion and exclusion criteria. There are different schools of thought for describing and classifying quadrilaterals according to their properties. For example, some mathematicians consider a parallelogram to be a trapezoid, since it has at least one pair of parallel sides; others prefer trapezoids to be in a separate class.
What follows is a list of some types of quadrilaterals:
Trapezoid
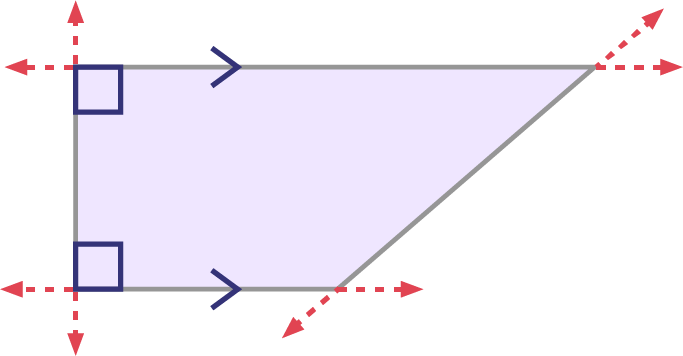
Parallelogram
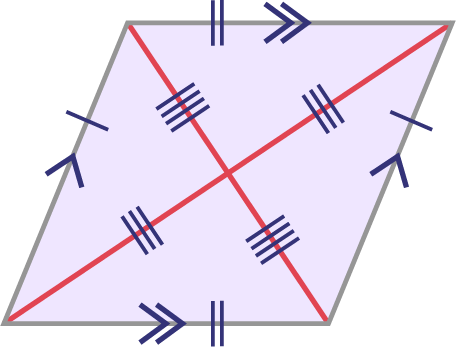Image a quadrilateral with two sets of equal sides. There are two oblique lines of different lengths which intersect in the centre of the figure.
Kite
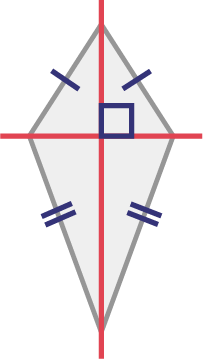Image Un quadrilateral with two sets of equal parallel sides. There is a vertical and a horizontal line intersecting in the centre of the shape, forming a square angle.
Rhombus
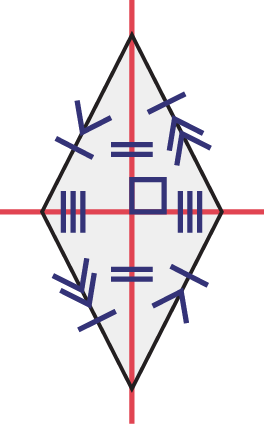Image a quadrilateral whose sides are all equal. There is a vertical and a horizontal line intersecting in the centre of the shape, forming a square angle.
Rectangle
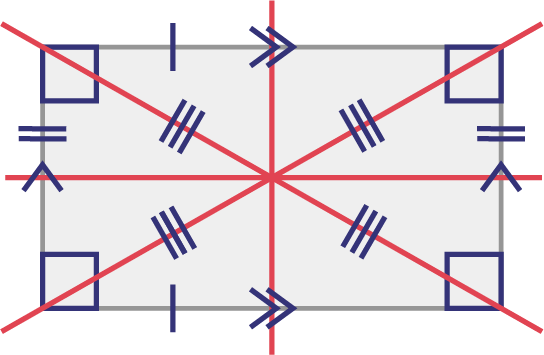Image a quadrilateral with two sets of equal parallel lines. There is a vertical and a horizontal line intersecting in the centre of the shape, and two oblique lines intersecting in the centre of the shape.
Square
Image a quadrilateral whose sides are all equal. Two oblique lines intersect in the centre of the shape, forming a square angle. The four square angles of the shape are indicated in the corners.
Deltoid
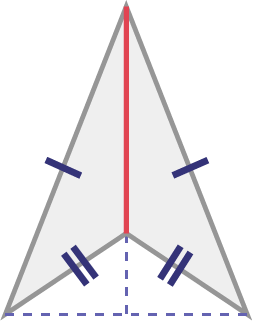
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Géométrie et sens de l'espace, Document d'appui, Fascicule 1, p. 34-36.
Knowledge: Diagonal
A line segment joining two non-adjacent vertices.
• Two congruent diagonals
• Two perpendicular diagonals
• Two diagonals that bisect each other.
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Géométrie et sens de l'espace, Document d'appui, Fascicule 1, p. 28.
Example
Knowledge: Rotational Symmetry
Rotational symmetry occurs when the position of a shape matches its original position after the shape has been rotated less than 360°. The order of rotational symmetry refers to the number of times the position of a shape matches its original position during a complete rotation around its centre.
Examples
Square
Image a series, of five squares, with a rotation point. Below the first square is written: starting position. Under the second square is written: quarter-turn rotation. Under the third square is written: half-turn rotation. Under the fourth square is written: three-quarter-turn rotation. Under the fifth square is written: complete rotation.
The square has a rotational symmetry of order 4.
Source: A Guide to Effective Instruction in Mathematics, Kindergarten to Grade 6, p. 47.
Rhombus
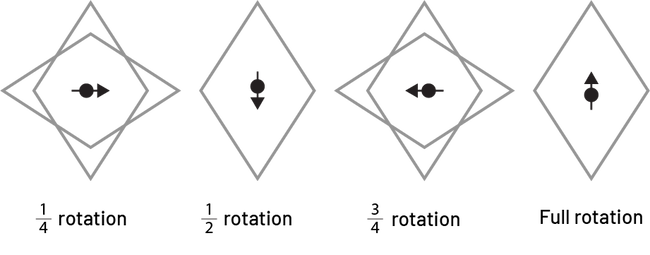Image Four sets of diamonds are presented. The first is a horizontal diamond superimposed on a vertical diamond. In the centre, there is an arrow pointing to the right. Under it is written: one quarter rotation. The second is a vertical diamond, with an arrow in the centre pointing down. Under it is written: one half rotation. The third is a horizontal diamond superimposed on a vertical diamond. The arrow in the centre points to the left. Under it is written: three quarter rotation. The fourth is a vertical diamond with the arrow in the centre pointing up. Under it is written: full rotation.
The rhombus has a rotational symmetry.
Rectangle
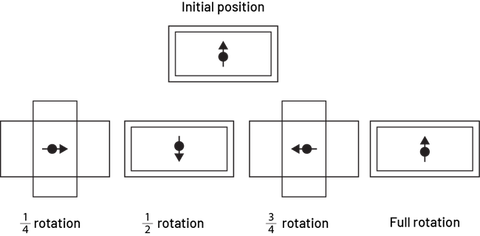Image Four sets of diamonds are presented. The first is a horizontal rectangle superimposed on a vertical rectangle. In the centre, there is an arrow pointing to the right. Under it is written: one quarter rotation. The second is a horizontal rectangle, with an arrow in the centre pointing down. Under it is written: one half rotation. The third is a horizontal rectangle superimposed on a vertical rectangle. The arrow in the centre points to the left. Under it is written: three quarter rotation. The fourth is a horizontal rectangle with the arrow in the centre pointing up. Under it is written: full rotation.
The rectangle has a rotational symmetry of order 2.
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
Knowledge: Line of Symmetry
A shape has reflection symmetry if one half of the shape is a reflection of the other half about a line called the line of symmetry. Shapes can have:
• A line of symmetry
• Two or more lines of symmetry
• No line of symmetry
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Géométrie et sens de l'espace, Document d'appui, Fascicule 1, p. 28.
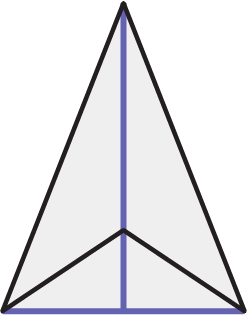
Example
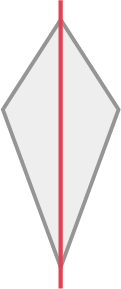
This kite has one line of symmetry.
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Géométrie et sens de l'espace, Document d'appui, Fascicule 1, p. 35.