E1.4 Décrire et effectuer des combinaisons de translations, de réflexions et de rotations jusqu’à 360° dans une grille, et prédire les résultats de ces transformations.
HABILETÉ : DÉCRIRE ET EFFECTUER DES TRANSLATIONS
Pour décrire et effectuer une translation oblique, par exemple, il faut vérifier à la fois le déplacement horizontal et le déplacement vertical. Pour ce faire, les élèves utilisent une notation symbolique entre parenthèses. Par exemple, une translation de trois unités vers la droite et de deux unités vers le bas est représentée symboliquement par (3D, 2B) ou (3 \(\rightarrow\), 2 \(\downarrow\)) ou (3, -2). Il est préférable d’habituer les élèves à toujours décrire la translation en indiquant d’abord le déplacement horizontal et ensuite le déplacement vertical.
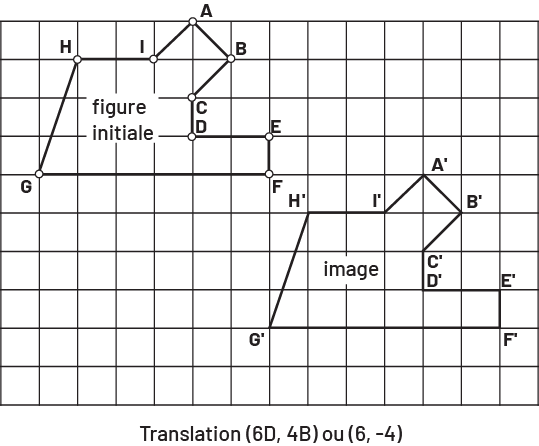Image Une grille dans laquelle se trouve deux figures. La première, soit la figure initiale, est
marquée par les points « a », « b », « c », « d », « e », « f », « g », « h », et « i ». La seconde, soit l’image, est
marquée par les points « a » prime, « b » prime, « c » prime, « d » prime, « e » prime, « f » prime, « g » prime, « h
» prime, et « i » prime. Sous la grille est écrit: translation (parenthèse ouvrante) six « d », quatre « b »
(parenthèse fermante) ou (parenthèse ouvrante) six, moins quatre (parenthèse fermante)
Les élèves peuvent décrire et effectuer des translations horizontales, verticales ou obliques définies à l’aide d’une flèche. Cette flèche peut être placée sur la figure ou à l’extérieur de la figure. La direction de la flèche correspond à la direction de la translation et sa longueur correspond à la grandeur du déplacement.
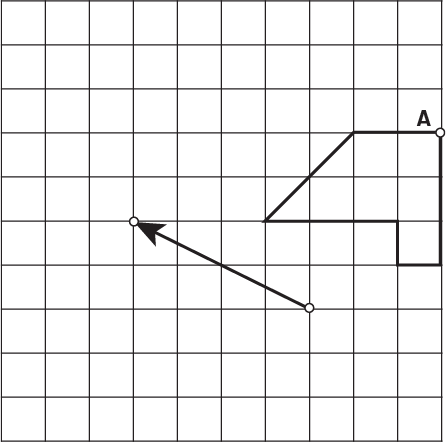
Pour décrire et effectuer la translation, les élèves doivent déterminer la grandeur des déplacements horizontal et vertical représentés par la flèche. Par exemple, la flèche ci-dessus définit la translation (4G, 2H), soit un déplacement de quatre unités vers la gauche et de deux unités vers le haut.
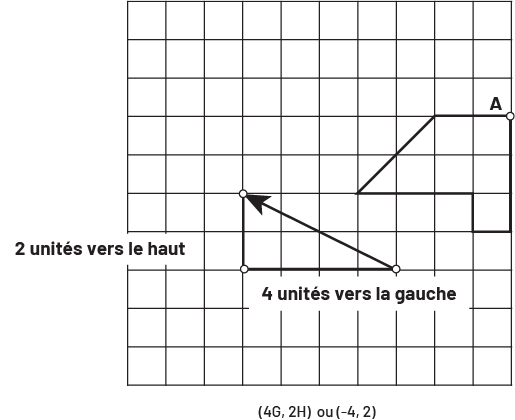Image Une grille dans laquelle se trouve une figure marquée par un point « a ». À la diagonale de la
figure, il y a une flèche oblique vers le haut à la gauche. La flèche forme un côté d’un triangle rectangle. Sur le
côté de ce triangle est écrit: deux unités vers le haut; sous le triangle est écrit: quatre unités vers la gauche.
Sous la grille est écrit: (parenthèse ouvrante) quatre « g », deux « h » (parenthèse fermante) ou (parenthèse
ouvrante) moins quatre, deux (parenthèse fermante).
Au moment d’une translation, tous les points de la figure initiale subissent le même déplacement, c’est-à-dire que tous les points de la figure initiale sont déplacés dans la même direction et sont équidistants des points correspondants de l’image.
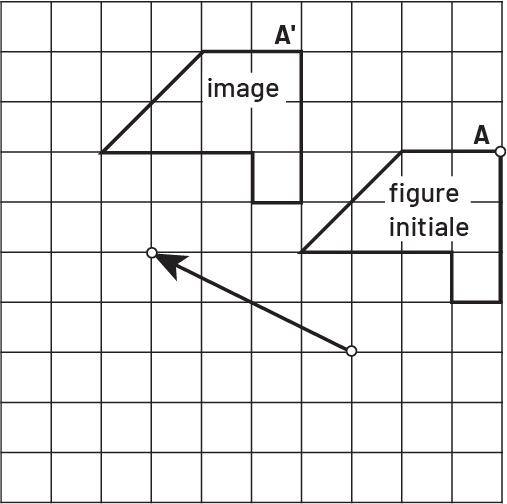Image Une grille dans laquelle se trouve deux figures. La première,
soit la figure initiale, est marquée par un point « a ». La seconde, soit l’image, est marquée par un point « a »
prime. Sous les figures, il y a une flèche oblique vers le haut à la gauche.
Chaque point de la figure initiale a subi une translation de 4 unités vers la gauche et de 2 unités vers le haut.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 28-30.
HABILETÉ : DÉCRIRE ET EFFECTUER DES RÉFLEXIONS
Pour décrire et effectuer une réflexion, il faut comprendre que tous les points sur la figure initiale et les points correspondants sur l’image sont à égale distance de l’axe de réflexion. La réflexion entraîne un changement de la position et de l’orientation originales d’une forme, mais l’image réfléchie est congruente à l’originale. En d’autres termes, l’image réfléchie a la même taille et la même forme, mais elle sera « orientée » dans une autre direction, et se trouvera dans une autre position. Il est important de noter que l’axe de réflexion peut être tracé dans n’importe quelle direction par rapport à la forme originale – horizontalement, verticalement ou diagonalement, selon n’importe quel angle.
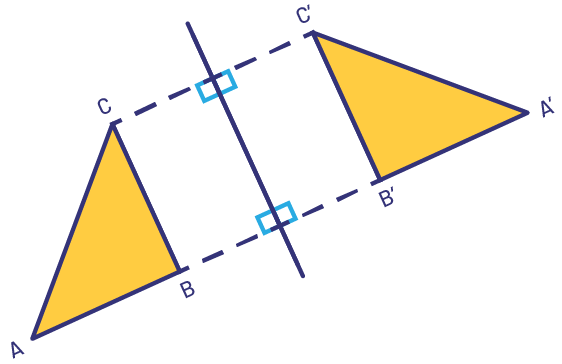Image Une figure composée d’un rectangle et deux triangles marqué par
les points « a », « b » et « c », et « a » prime, « b » prime et « c » prime respectivement. Il y a une ligne qui
passe à travers le centre du rectangle. Quatre angles rectangles sont identifiés dans la figure.
Source : A Guide to Effective Instruction in Mathematics, Kindergarten to Grade 6, p. 35.
Les élèves effectuent des réflexions de figures simples et complexes (par exemple, pour créer des frises et des dallages) sur du papier à points et du papier quadrillé, à l’aide d’un Mira, de papier calque ou d’un logiciel ou d’une application de géométrie dynamique.
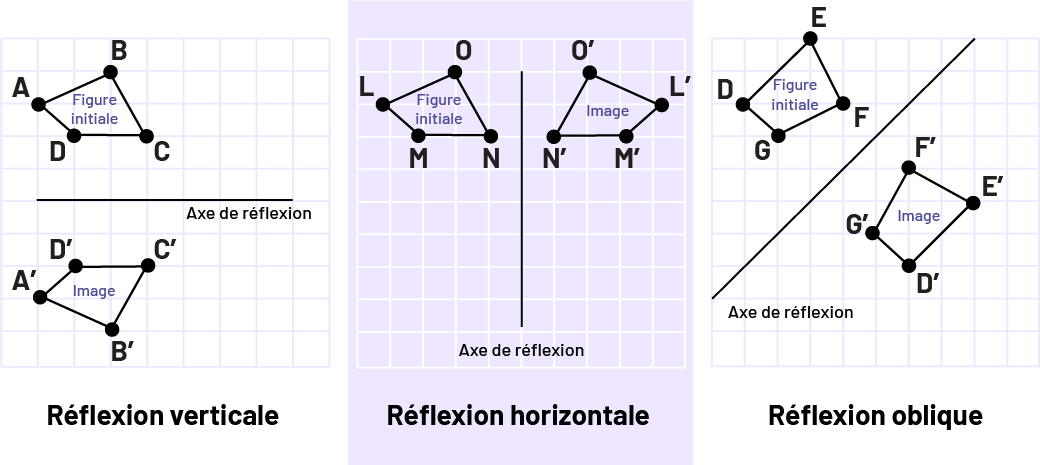Image Il y a trois grilles représentant une réflexion verticale, une
réflexion horizontale, et une réflexion oblique. Dans la première grille, il y a deux figures, soit la figure initiale
et l’image, d’un côté chaque d’une ligne horizontale, soit l’axe de réflexion. Dans la deuxième grille, il y a deux
figures, soit la figure initiale et l’image, d’un côté chaque d’une ligne verticale, soit l’axe de réflexion. Dans la
troisième grille, il y a deux figures, soit la figure initiale et l’image, d’un côté chaque d’une ligne oblique, soit
l’axe de réflexion.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 31.
HABILETÉ : DÉCRIRE ET EFFECTUER DES ROTATIONS JUSQU’À 360° DANS UNE GRILLE
Pour décrire et effectuer une rotation, il faut comprendre et indiquer :
1. l’emplacement du centre de rotation (par exemple, un point sur le contour de la figure, à l’intérieur de la figure ou à l’extérieur de la figure);
2. la mesure de la rotation (par exemple, un quart de tour ou 90°, un demi-tour ou 180°, trois quarts de tour ou 270° ou un tour ou 360°);
3. le sens de la rotation (par exemple, dans le sens des aiguilles d’une montre, dans le sens contraire des aiguilles d’une montre).
Les élèves doivent comprendre ce que représente une rotation d’un quart de tour, d’un demi-tour et de trois quarts de tour dans le sens des aiguilles d’une montre ou dans le sens contraire des aiguilles d’une montre. Il est important de leur présenter diverses activités kinesthésiques qui leur permettent de développer cette compréhension.
L’utilisation de l’horloge (par exemple, une horloge en carton avec deux aiguilles fixées à l’aide d’une attache parisienne) est une stratégie efficace pour aider les élèves à développer le sens des fractions de tour. Les élèves placent d’abord les aiguilles à 12. Pour représenter une rotation d’un quart de tour dans le sens des aiguilles d’une montre, elles et ils déplacent l’aiguille des minutes à 3. L’aiguille des heures représente la direction initiale alors que celle des minutes représente la direction après la rotation.
Les élèves peuvent faire le lien entre la fraction de tour de rotation de la grande aiguille d’une horloge, le nombre de minutes et le nombre de degrés. Par exemple, une rotation d’un quart de tour de la grande aiguille correspond à 15 minutes ou à 90°.
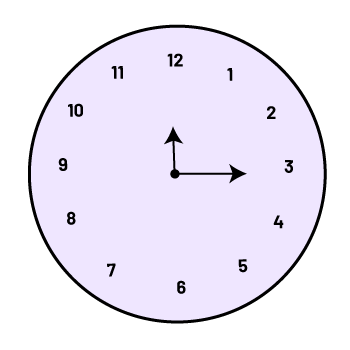
15 minutes = \(\frac{1}{4}\) de tour = 90°
Note : Sur une véritable horloge, cette correspondance n’est pas tout à fait exacte puisque l’aiguille des heures se déplace légèrement lorsque l’aiguille des minutes effectue une rotation d’un quart de tour.
Il importe encore une fois de varier la direction initiale des aiguilles. Par exemple, le personnel enseignant peut placer les deux aiguilles de l’horloge à 2 et demander aux élèves d’effectuer une rotation d’un demi-tour dans le sens des aiguilles d’une montre. Les élèves peuvent alors se baser sur le fait qu’une rotation d’un demi-tour de la grande aiguille correspond à 180° ou à 30 minutes pour déterminer que l’aiguille des minutes doit être placée à 8.
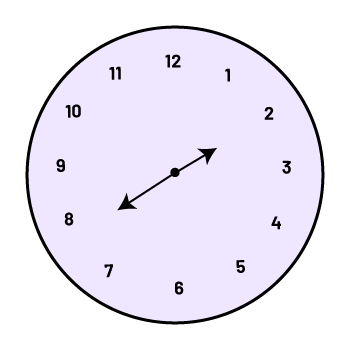
30 minutes = \(\frac{1}{2}\) tour = 180°
Une fois que les élèves ont développé leur compréhension des fractions de tour à l’aide de matériel concret, elles et ils sont en mesure de les représenter sur des cercles tracés sur papier.
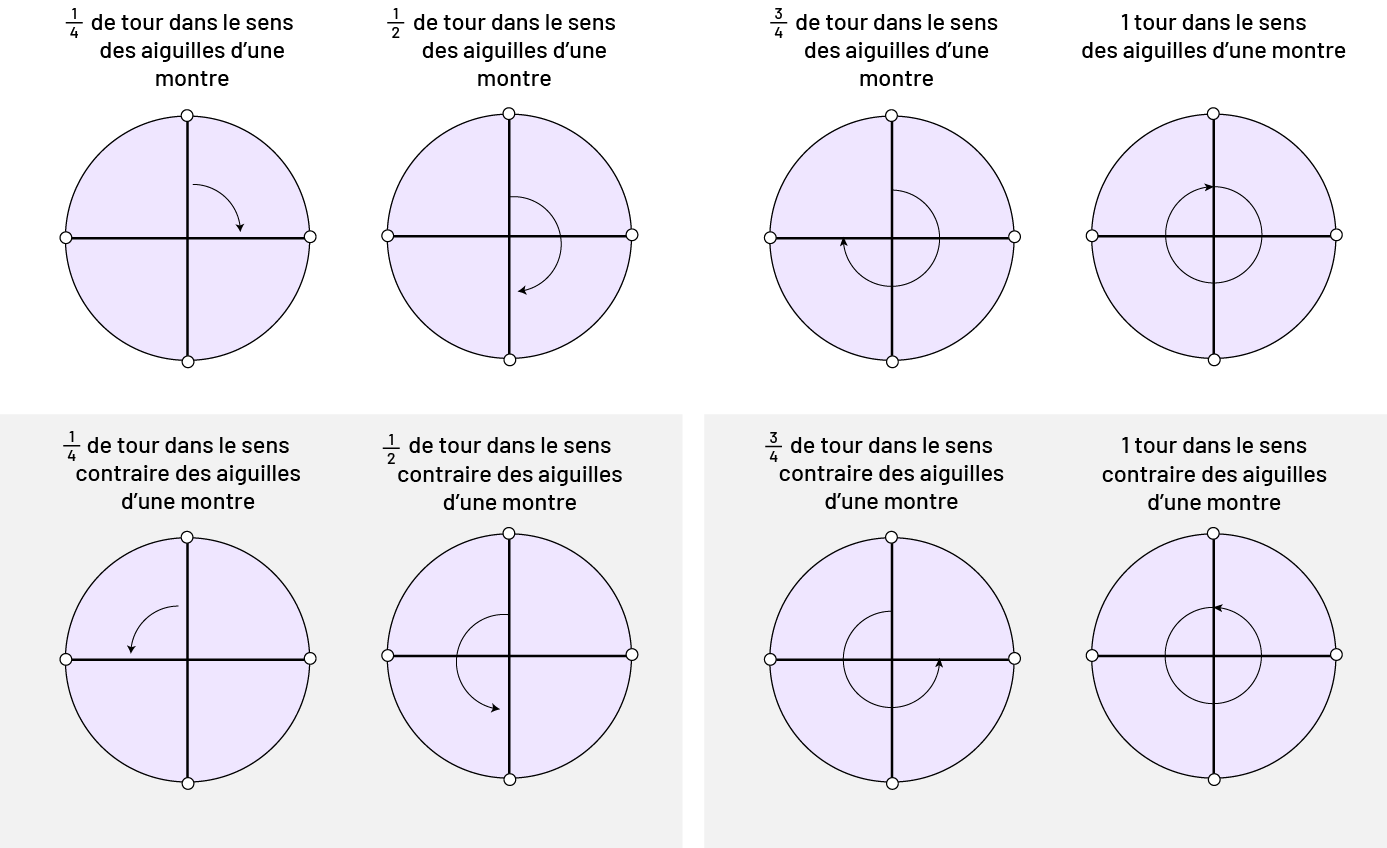Image Il y a huit cercles divisés en quart. Il y a une flèche courbée vers le bas dans le premier
quadrant du premier cercle. Au-dessus est écrit: un quart de tour dans le sens des aiguilles d’une montre. Il y a une
flèche
courbée vers le gauche passant dans le premier et le quatrième quadrant du deuxième cercle. Au-dessus est écrit: un
demi-tour dans le sens des aiguilles d’une montre. Il y a une flèche courbée vers le haut passant dans le premier,
le quatrième et le troisième quadrant du troisième cercle. Au-dessus est écrit: trois quart de tour dans le sens des
aiguilles d’une montre. Il y a un plus petit cercle complet dans le quatrième cercle. Au-dessus est écrit: un tour
dans le sens des aiguilles d’une montre.Il y a une flèche courbée vers le bas dans le deuxième quadrant du cinquième
cercle. Au-dessus est écrit: un quart
de tour dans le sens contraire des aiguilles d’une montre. Il y a une flèche courbée vers le gauche passant dans le
deuxième et le troisième quadrant du sixième cercle. Au-dessus est écrit: un demi-tour dans le sens contraire des
aiguilles d’une montre. Il y a une flèche courbée vers le haut passant dans le deuxième, le troisième et le
quatrième quadrant du troisième cercle. Au-dessus est écrit: trois quart de tour dans le sens contraire des
aiguilles d’une montre. Il y a un plus petit cercle complet dans le huitième cercle. Au-dessus est écrit: un tour
dans le sens contraire des aiguilles d’une montre.
Les élèves doivent effectuer des rotations de figures en utilisant un des sommets de la figure comme centre de rotation. L’utilisation de divers outils (par exemple, papier calque, papier à coordonnées polaires, équerre, logiciel ou application de géométrie dynamique) pour effectuer la rotation selon la fraction de tour spécifiée aide les élèves à mieux comprendre cette transformation. Les élèves effectuent aussi des rotations dont le centre est situé sur le contour ou à l’intérieur de la figure, et des rotations dont le centre est situé à l’extérieur de la figure.
Exemple
Rotation d’un quart de tour dans le sens des aiguilles d’une montre, avec le centre de rotation :
- sur un sommet de la figure;
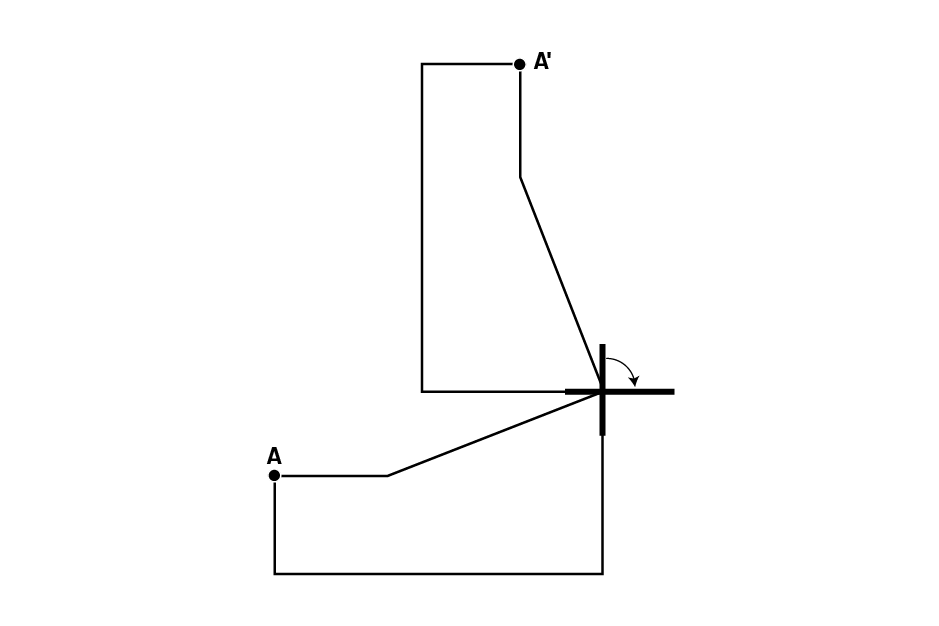
- sur le contour de la figure ou à l’intérieur de la figure;
Image Il y a deux ensembles de figures congrues d’orientation différente. Dans le premier ensemble, la
première figure est marquée par un point « a » et la seconde par un point « a » prime. Les deux figures sont
connectées à la base. Dans le second ensemble, la première figure est marquée par un point « a » et la seconde par un
point « a » prime. Les deux figures se croisent au centre.
- à l’extérieur de la figure.
Image Il y a deux figures congrues d’orientation différente. La première figure est marquée par un
point « a ». La seconde figure est marquée par un point « a » prime. Il y a une croix inversée entre les deux figures.
Dans le premier quadrant de la croix, il y a une flèche arrondie qui point vers le bas.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 32-35.
HABILETÉ : DÉCRIRE ET EFFECTUER DES COMBINAISONS DE TRANSLATIONS, DE RÉFLEXIONS ET DE ROTATIONS JUSQU’À 360° DANS UNE GRILLE
Les stratégies d’enseignement de la position et du mouvement au cycle moyen doivent être axées sur la compréhension des relations spatiales. L’emplacement d’un point est lié à la fois à une position horizontale et à une position verticale. Les transformations sont liées les unes aux autres – par exemple, la position d’une image après une rotation peut souvent être reproduite par une combinaison d’autres transformations. Bien que la position et le mouvement puissent être traités comme des composantes distinctes d’un programme d’enseignement du cycle moyen, lorsqu’ils sont enseignés en combinaison avec un accent mis sur les relations, les élèves sont capables d’établir d’importants liens mathématiques.
Source : A Guide to Effective Instruction in Mathematics, Kindergarten to Grade 6, p. 61.
L’élève décrit et effectue les changements subit par une figure initiale lorsqu’elle est transformée à l’aide d’une translation, d’une réflexion et d’une rotation. Les combinaisons peuvent inclure deux transformations ou plus d’une figure et sont effectuées sur une grille qui permet à l’élève d’indiquer, à l’aide du vocabulaire approprié, les déplacements d’une case de la grille à une autre de la figure initiale. Les logiciels ou les applications de géométrie dynamique peuvent aider les élèves à visualiser le fonctionnement de combinaisons de transformations.
Exemple
La figure initiale subit une translation de six unités vers la droite et une rotation de 180° dans le sens des aiguilles d’une montre sur un point à l’extérieur de la figure.
Image Il y a trois figures. La première est marquée par un point « a » à un des sommets. La deuxième
figure est marquée par un point « a » prime. La troisième figure est inversée et marquée par un point « a » double
prime. La deuxième et la troisième figures sont liés par deux lignes de longueur différentes qui s’intersecte à un
centre de rotation. Sous les deux premières figures, il y a une flèche horizontale.
Source : adapté de Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 37.
HABILETÉ : PRÉDIRE LES RÉSULTATS DES TRANSFORMATIONS
Au cycle moyen, les élèves prédisent le résultat des transformations et décrivent ce qui arrive à l’objet au fur et à mesure que sont effectuées les transformations. Grâce à des observations guidées, les élèves seront ultimement capables d’observer l’orientation initiale d’un objet et le résultat de plusieurs transformations, et de décrire les transformations effectuées sans les voir se produire.
Source : A Guide to Effective Instruction in Mathematics, Kindergarten to Grade 6, p. 34.
CONNAISSANCE : TRANSLATION
La translation est définie par sa grandeur et sa direction (représentées symboliquement par des coordonnées ou par une flèche). Elle représente un déplacement linéaire, horizontal, vertical ou oblique dans lequel la figure initiale et l’image sont congruentes. La distance entre chaque point sur la figure initiale et le point correspondant sur l’image est constante. L’orientation de l’image est la même que l’orientation de la figure initiale.
CONNAISSANCE : RÉFLEXION
Une réflexion est un déplacement réflexif perpendiculaire à un axe de réflexion. Chaque point sur la figure initiale et le point correspondant sur l’image sont à la même distance de l’axe de réflexion. La figure initiale et l’image sont congruentes, mais l’orientation de l’image est différente de l’orientation de la figure initiale.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 36.
CONNAISSANCE : ROTATION
Une rotation est une transformation qui déplace chaque point d'une forme ou d'une figure autour d'un point fixe, appelé centre de rotation. Une rotation crée une image qui est congruente à la forme d'origine. Toutefois, l’orientation de l’image est différente de l’orientation de la figure initiale.
Le centre de rotation peut se retrouver n'importe où sur le plan, soit à l'extérieur de la figure, soit à l'intérieur.
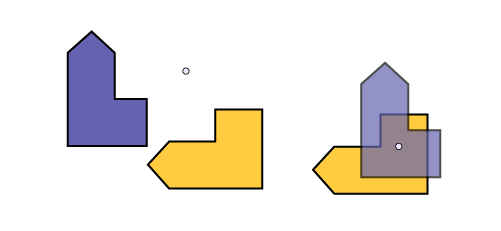Image Il
y a deux ensembles de figures. Dans la première, il y a deux figures congrues à orientation différent. Entre les deux
figures, il y a un point. Dans le second ensemble, les deux figures sont super-imposé et il y a un point au centre des
deux figures.
Lorsque le centre de rotation se retrouve sur un sommet de la figure, la figure initiale et son image partageront ce point.
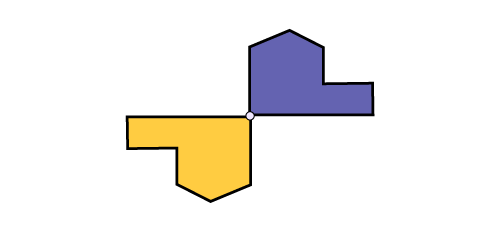
Source : A Guide to Effective Instruction in Mathematics, Kindergarten to Grade 6, p. 36.
CONNAISSANCE : COMBINAISON DE TRANSFORMATIONS
Une combinaison de transformations est une séquence de figures obtenues à la suite de diverses transformations successives, telles que des translations, des réflexions et des rotations.
Exemple
La figure initiale subit une réflexion par rapport à un axe de réflexion vertical et une translation de six unités vers la droite et de deux unités vers le bas.
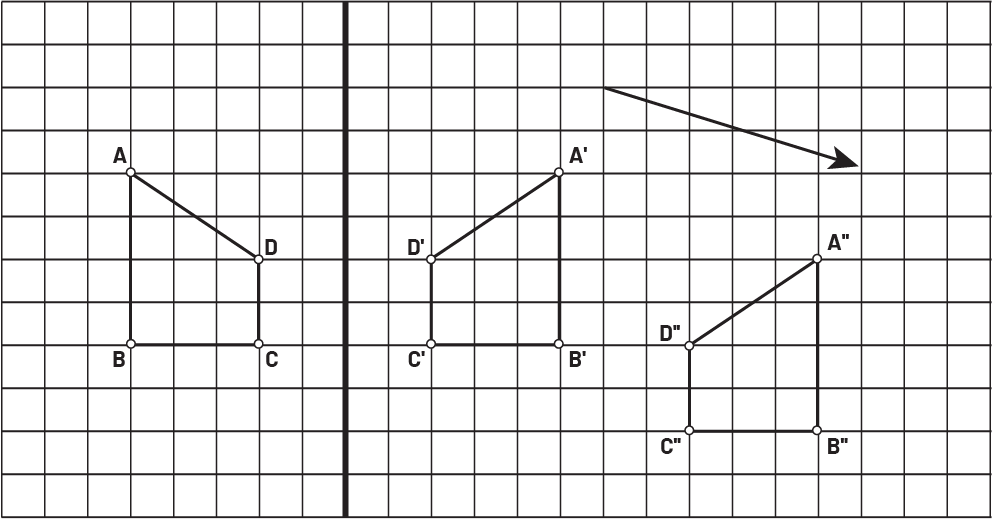Image Il y a une grille divisée en deux sections. Dans la
première section, il y a une figure marquée par les points « a », « b », « c » et « d ». De l’autre côté, il y a la
figure inverse de celle du premier côté, marquée par les points « a » prime, « b » prime, « c » prime et « d » prime.
À la diagonale, il y a une deuxième figure congrue marquée par les points « a » double prime, « b » double prime, « c
» double prime et « d » double prime. Au-dessus, il y a une flèche oblique vers la droite.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 31.