E1.4 Describe and perform combinations of translations, reflections, and rotations up to 360° on a grid, and predict the results of these transformations.
Skill: Describing and Performing Translations
To describe and perform an oblique translation, for example, one must verify both the horizontal movement and the vertical movement. To do this, students use symbolic notation in parentheses. For example, a translation of three units to the right and two units down is represented symbolically by 3 right, 2 down or (3 \(\rightarrow\), 2 \(\downarrow\)) or (x + 3, y -2). It is best to get the students used to always describing the translation by first indicating the horizontal movement and then the vertical movement.
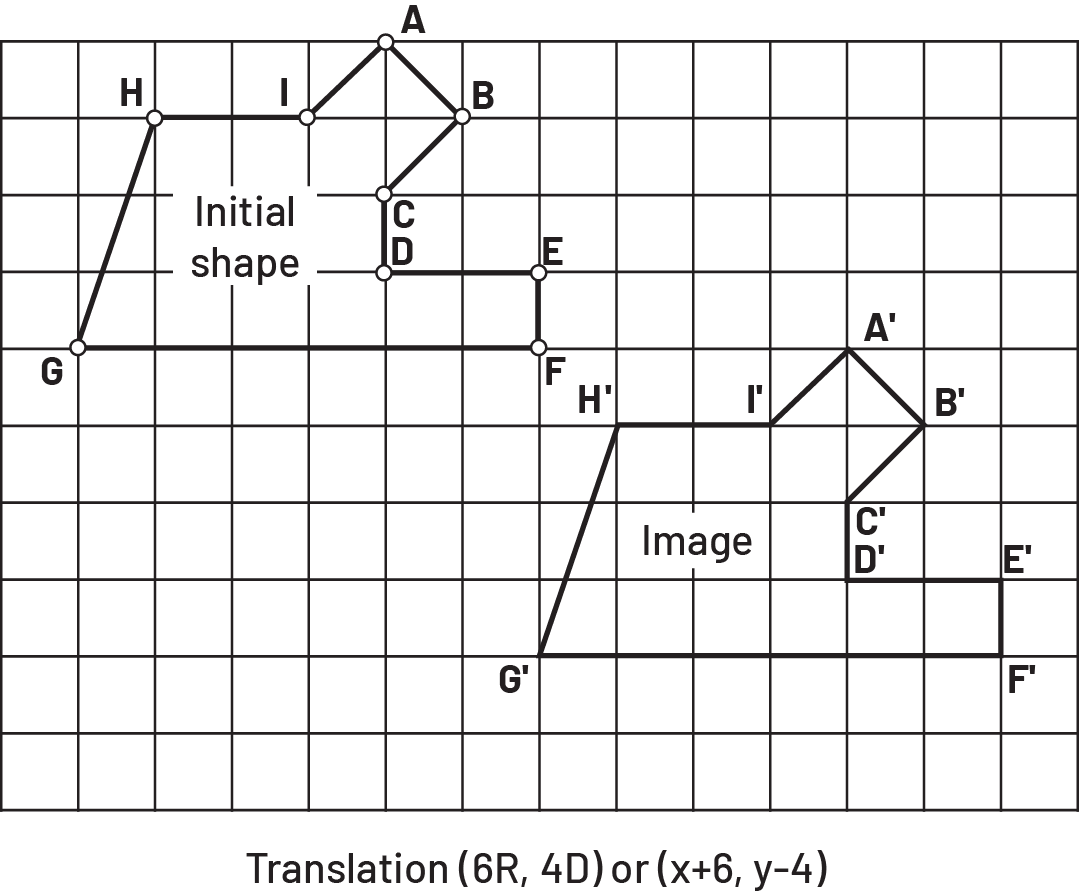Image A grid in which there are two figures. The first, being the initial figure, is marked by the points “ a ”, “ b ”, “ c ”, “ d ”, “ e ”, “ f ”, “ g ”, “ h ” and “ i ”. The second, being the image, is marked by the points “ a ” prime, “ b ” prime, “ c ” prime, “ d ” prime, “ e ” prime, “ f ” prime, “ g ” prime, “ h ” prime and “ i ” prime. Below the grid is written: translation (opening parenthesis) six “ d ”, four “ b ” (closing parenthesis) or (opening parenthesis) six, minus four (closing parenthesis).
Students can describe and perform horizontal, vertical, or oblique translations defined with an arrow. The arrow can be placed on the shape or outside the shape. The direction of the arrow corresponds to the direction of the translation and its length corresponds to the size of the movement.
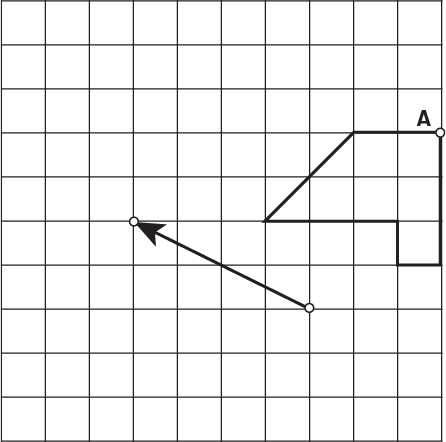Image a grid in which there is a figure marked by a point “a ”. To the diagonal of the figure, there is an oblique arrow towards the upper left.
To describe and perform the translation, students must determine the size of the horizontal and vertical movements represented by the arrow. For example, the arrow in the following plane describes the translation 4 left, 2 up.
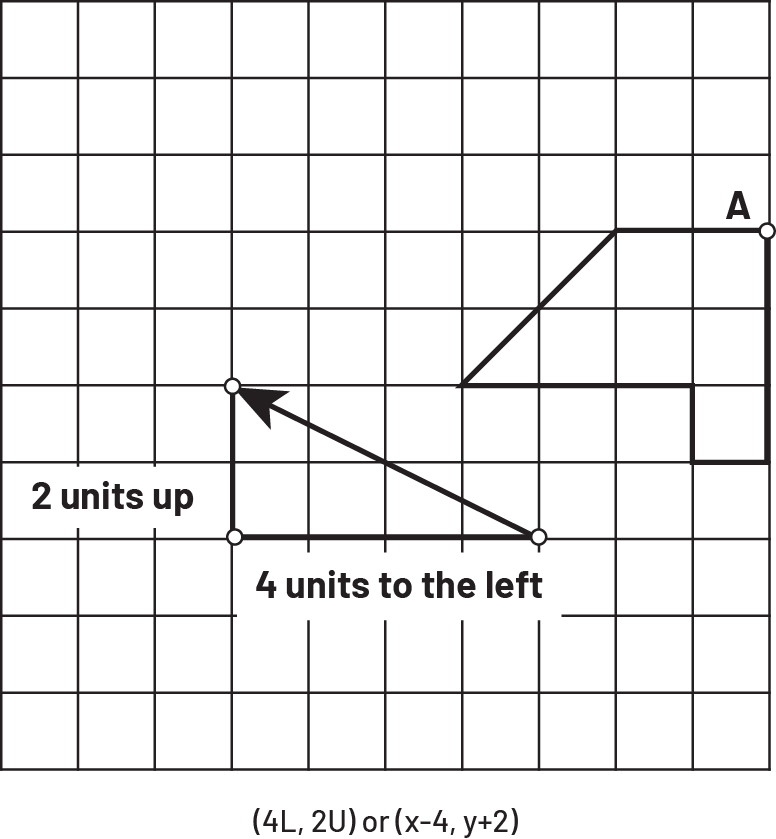Image a grid in which there is a figure marked by a point “ a ”. To the diagonal of the figure, there is an oblique arrow towards the upper left. The arrow forms one side of a right-angled triangle. On the side of the triangle is written: two units upwards; below the triangle is written: four units to the left. Below the grid is written (opening parenthesis) four “ g ”, two “ h ”(closing parenthesis) or (opening parenthesis) minus four, two (closing parenthesis).
During a translation, all the points of the original shape undergo the same movement, and all the points of the original shape are moved in the same direction, so all the points of the image are equidistant from the corresponding points of the original shape.
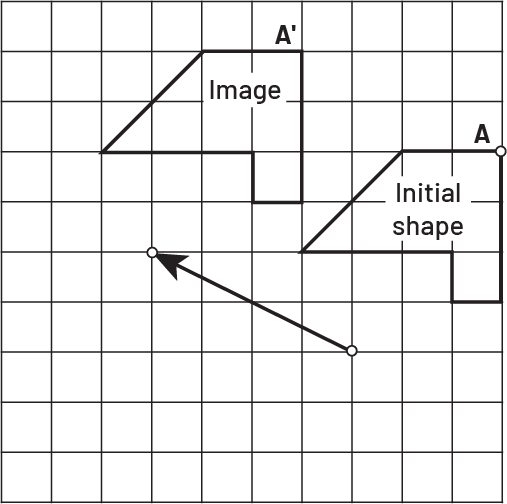Image A grid in which there are two figures. The first, being the initial figure, is marked by a point “ a ”. The second, being the image, is marked by a point “ a ” prime. Below the figure, there is an oblique arrow towards the upper left.
Each point of the original shape has undergone a translation of 4 units to the left and 2 units up.
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 2, p. 28-30.
Skill: Describing and Performing Reflections
To describe and perform a reflection, it is necessary to understand that all the points on the original shape and the corresponding points on the image are equidistant from the line of reflection. The reflection results in a change in the original position and orientation of a shape, and the reflected image is congruent with the original. In other words, the reflected image is the same size and shape, but it will be ”oriented“ in a different direction, and will be in a different location. It is important to note that the line of reflection can be drawn anywhere - horizontally, vertically, or diagonally, at any angle.
Image a figure made up of a rectangle and two triangles marked by the points “ a ”, “ b ” and “ c ”, and the points “ a ” prime, “ b ” prime and “ c ” prime respectively. There is a line passing through the centre of the rectangle. Four square angles are indicated in the figure.
Source: A Guide to Effective Instruction in Mathematics, Kindergarten to Grade 6, p. 35.
Students perform reflections of simple and complex shapes (for example, to create friezes and tessellations) on dot paper or grid paper, using a Mira, tracing paper, or dynamic geometry software or application.
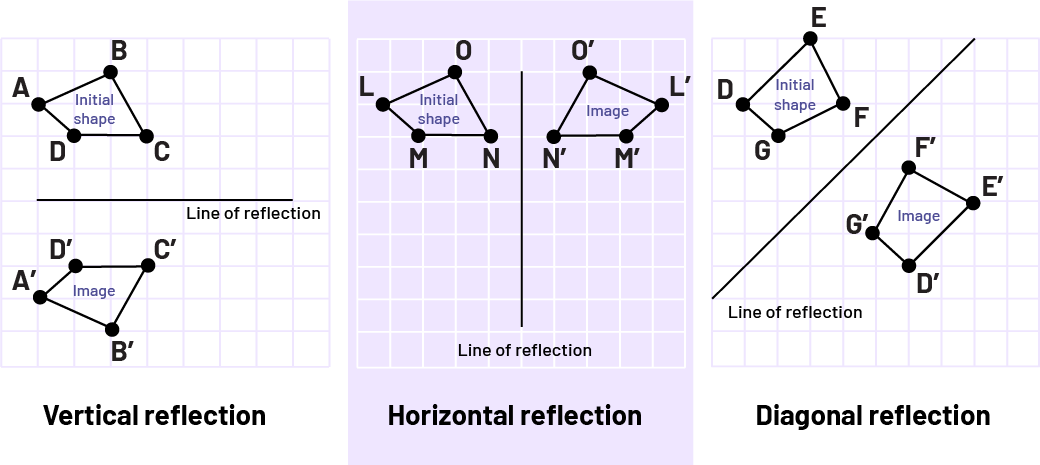Image there are three grids representing a vertical reflection, a horizontal reflection, and an oblique reflection. In the first grid, there are two figures, the initial figure and the image, of one side each of a horizontal line, being the line of reflection. In the second grid, there are two figure, the initial figure and the image, or one side each of a vertical line, being the line of reflection. In the third image, there are two figure, the initial figure and the image, of one side each of an oblique line, being the line of reflection.
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 2, p. 31.
Skill: Describing and Perform Rotations up to 360° on a Grid
To describe and perform a rotation, you must understand and state:
- the location of the centre of rotation (for example, a point on the outline of the shape, inside the shape, or outside the shape);
- the measurement of rotation (for example, a quarter turn or 90°, a half turn or 180°, a three-quarter turn or 270°, or a full turn or 360°);
- the direction of rotation (for example, clockwise, counterclockwise).
Students need to understand what a quarter, half, and three-quarter turn clockwise or counterclockwise represents, and it is important to introduce them with a variety of kinesthetic activities that help them develop this understanding.
Using the clock as a model is an effective strategy to help students develop a sense of how a full revolution can be represented using fractions. For examples, students could use a cardboard clock made with two hands attached using a brass fastener. Ask students to place both hands at 12. Then, to represent a rotation of one quarter-turn clockwise, ask students to move the minute hand to 3. The hour hand represents the initial position while the minute hand represents the position after the rotation.
Students can relate the fraction of a turn of the large clock hand to the number of minutes and the number of degrees. For example, a quarter turn of the large hand is 15 minutes or 90°.
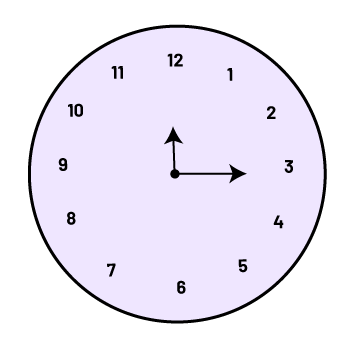
15 minutes = \(\frac{1}{4}\) turn = 90°
Note: On a real clock, this correspondence is not quite exact since the hour hand moves slightly when the minute hand rotates a quarter turn.
Again, it is important to vary the initial direction of the hands. For example, teachers can place both hands of the clock at 2 and have students rotate the minute hand clockwise one-half turn. Students can then use the fact that a one-half turn of the minute hand is 180° or 30 minutes to determine that the minute hand should be placed at 8.
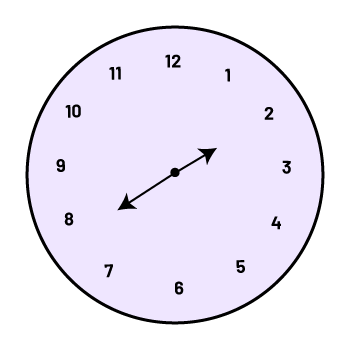
30 minutes = \(\frac{1}{2}\) turn = 180°
Once students have developed their understanding of fractions of a turn using concrete materials, they are able to represent them on circles drawn on paper.
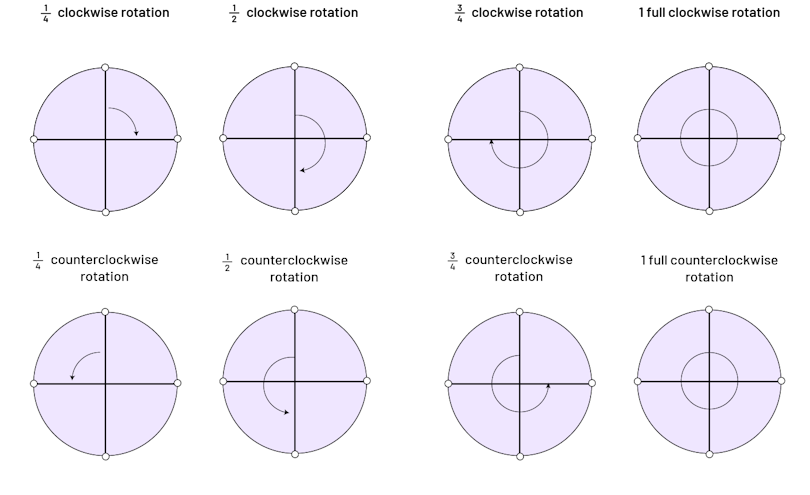Image there are eight circles divided in quarters. There is a curved arrow in the first quadrant of the first circle. Above is written: a quarter clockwise rotation of the needles of a watch. There is a curved arrow passing through the first and fourth quadrants of the second circle. Above is written: a half clockwise rotation of the needles of a watch. There is a curve arrow passing through the first, fourth, and third quadrants. Above is written: three-quarter clockwise rotation of the needles of a watch. There is a smaller circle in the fourth circle. Above is written: one full clockwise rotation of the needles of a watch. There is a curved arrow in the second quadrant of the first circle. Above is written: a quarter counter-clockwise rotation of the needles of a watch. There is a curved arrow passing through the second and third quadrants of the second circle. Above is written: a half counter-clockwise rotation of the needles of a watch. There is a curve arrow passing through the second, third, and fourth quadrants. Above is written: three-quarter counter-clockwise rotation of the needles of a watch. There is a smaller circle in the fourth circle. Above is written: one full counter-clockwise rotation of the needles of a watch.
Students should perform rotations of shapes using one of the vertices of the shape as the centre of rotation. Using a variety of tools (for example, tracing paper, polar coordinate graph paper, square grid paper, dynamic geometry software or application) to perform the rotation according to the specified fraction of a revolution helps students better understand this transformation. Students should also perform rotations with the centre on the perimeter of the shape or inside of the shape, and rotations with the centre outside the shape.
Example
Rotation of a quarter turn clockwise, with the centre of rotation.
- on a vertex of the shape;
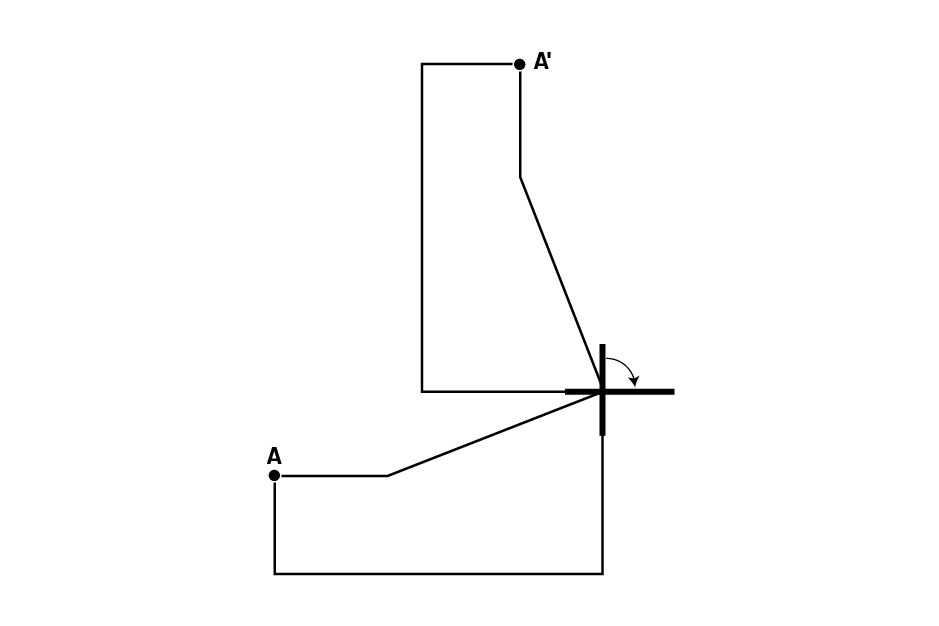Image There are two congruous figures with different orientations connect at a peak. The first figure is marked by a point “ a ”. The second figure is marked by a point “ a ” prime.
- on the perimeter of the shape or inside the shape;
Image There are two sets of congruous figures with different orientations. In the first set, the first figure is marked by a point “ a ” and the second by a point “ a ” prime. The two figures are connected at the base. In the second set, the first figure is marked by a point “ a ” and the second by a point “ a ” prime. The two figures intersect in the middle.
- outside the shape.
Image there are two congruous figures with different orientations. The first figure is marked by a point “ a ”. The second figure is marked by a point “ a ” prime. There is an inversed cross between the two figures. In the first quadrant of the cross, there is a rounded arrow pointing towards the bottom.
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 2, p. 32-35.
Skill: Describing and Performing Combinations of Translations, Reflections, and Rotations of up to 360° on a Grid
Strategies for teaching location and movement in the junior grades should focus on understanding spatial relationships. The location of a point is related to both a horizontal and a vertical position. Transformations are related to each other - for example, the location of an image after a rotation can often be reproduced by a combination of other transformations. Although location and movement can be treated as separate components, when taught in combination with a focus on relationships, students are better able to make important mathematical connections.
Source: A Guide to Effective Instruction in Mathematics, Kindergarten to Grade 6, p. 61.
The student describes and performs the changes undergone by an original shape when it is transformed using a translation, a reflection, and a rotation. The combinations may include two or more transformations of a shape and are performed on a grid which allows the student to indicate, using the appropriate vocabulary, the movements of the original shape from one point or square of the grid to another. Dynamic geometry software or applications can help students visualize how combinations of transformations work.
Example
The original shape (A) is translated six units to the right (A’) and rotated around a point outside the shape 180° clockwise (A’’).
Image There are three figures. The first is marked by a point “ a ” at one of the peaks. The second figure is marked by a point “ a ” prime. The third figure is inversed and marked by a point “ a ” double prime. The second and third figures are linked by two lines of different lengths which intersects at a rotation point. Under the two first figures, there is a horizontal arrow.
Source: adapted and translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 2, p. 37.
Skill: Predicting the Results of Transformations
In the junior grades, students predict the outcome of transformations and describe what happens to a shape as the transformations are performed. Through guided observations, students will ultimately be able to observe the initial orientation of the shape and the outcome after several transformations, and describe the transformations performed without seeing them occur.
Source: A Guide to Effective Instruction in Mathematics, Kindergarten to Grade 6, p. 34.
Knowledge: Translation
The translation is defined by its size and direction (represented symbolically by coordinates or by an arrow). It represents a linear, horizontal, vertical, or oblique movement in which the original shape and the image are congruent. The distance between each point on the original shape and the corresponding point on the image is constant. The orientation of the image is the same as the orientation of the original shape.
Knowledge: Reflection
A reflection is a flip performed over to a line of reflection. Each point on the original shape and the corresponding point on the image are at the same distance from the line of reflection. The original shape and the image are congruent, but the orientation of the image is different from the orientation of the original shape.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 2, p. 36.
Knowledge: Rotation
A rotation is a transformation that moves each point of a shape around a fixed point, called the centre of rotation. A rotation creates an image that is congruent with the original shape. However, the orientation of the image is different from the orientation of the original shape.
The centre of rotation can be anywhere on the plane, either outside the shape or inside.
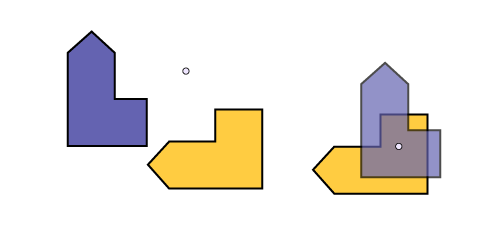Image There are two sets of figures. In the first, there are two congruous figures with different orientations. Between the two figures there is a point. In the second, the two figures are superimposed and there is a point in the centre of the two figures.
When the centre of rotation is on a vertex of the shape, the original shape and its image will share this point.
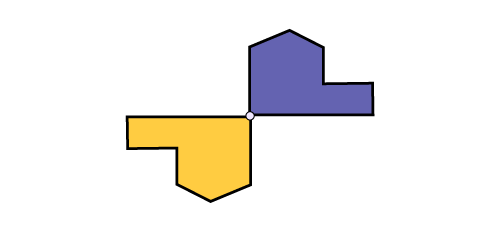
Source: A Guide to Effective Instruction in Mathematics, Kindergarten to Grade 6, p. 36.
Knowledge: Combination of Transformations
A combination of transformations such as translations, reflections, and rotations applied to a shape that results in an image of that shape following the application of a sequence of transformations, such as translations, reflections, and rotations.
Example
The original shape undergoes a reflection about a vertical line of reflection (A’) and a translation of six units to the right and two units downwards (A’’)..
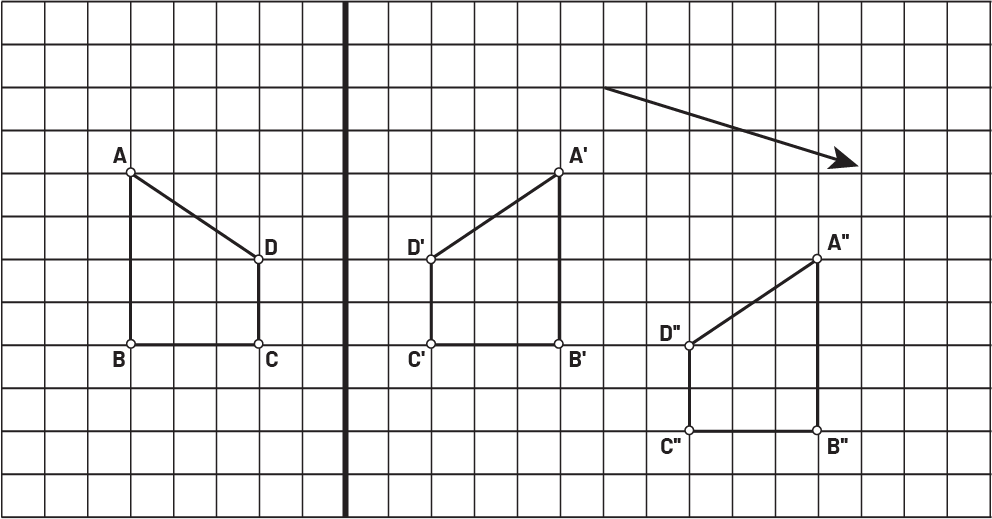Image there is a grid divided in two sections. In the first section, there is a figure marked by the points “ a ”, “ b ”, “ c ” and “ d ”. On the other side, there is an inversed figure to the one on the first side, marked by the points “ a “ prime, “ b ” prime, “ c ” prime et “ d ” prime. To the diagonal, there is a second congruous figure marked by the points “ a ” double prime, “ b ” double prime, “ c ” double prime and “ d ” double prime. Below, there is an oblique arrow to the right.
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 2, p. 31.