E2.5 Créer et utiliser les développements de solides pour déterminer les relations entre les faces de prismes et de pyramides, et leur aire totale.
HABILETÉ : DÉTERMINER LES RELATIONS ENTRE LES FACES ET L’AIRE TOTALE
L’aire totale est la somme des aires de toutes les faces d’un solide.
L’aire est additive : des aires partielles peuvent être additionnées pour trouver une aire complète. Pour trouver l’aire totale d’un prisme ou d’une pyramide, il faut se servir du concept fondamental d’additivité.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère
de l’Éducation de l’Ontario.
Additivité
L’élève qui comprend ce concept réalise que l’aire d’une figure est égale à la somme de l’aire de chacune de ses parties. De même, l’aire totale d’un solide est égale à la somme de l’aire de chacune de ses faces.
Source : Fiche de la 4e à la 6e année_Attribut aire, p. 3.
CONNAISSANCE : PRISME
Les faces latérales d’un prisme sont des parallélogrammes. Il possède au moins six sommets et cinq faces. Le prisme droit a des arêtes latérales perpendiculaires à sa base. Le prisme oblique a des arêtes latérales qui ne sont pas perpendiculaires à sa base.
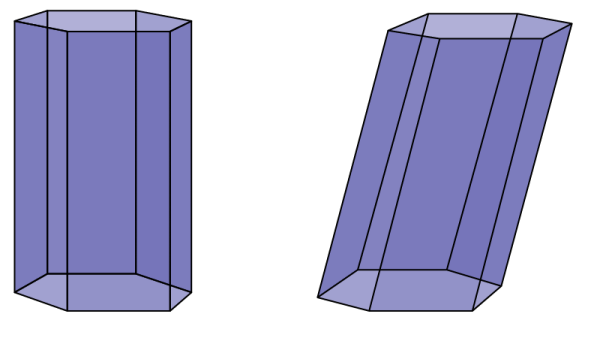
Plus le nombre de côtés de la base augmente, plus le prisme ressemble à un cylindre.

Propriétés suffisantes d’un prisme
Polyèdre ayant deux bases polygonales parallèles et congruentes.
La base du prisme détermine son nom.
- Triangle : prisme à base triangulaire
- Carré : prisme à base carrée
- Rectangle : prisme à base rectangulaire
- Pentagone : prisme à base pentagonale
- Hexagone : prisme à base hexagonale
- Octogone : prisme à base octogonale
- Ennéagone : prisme à base ennéagonale
- Décagone : prisme à base décagonale
Examiner le nombre de côtés de la base d’un prisme peut aider les élèves à en prédire le nombre de faces, d’arêtes et
de sommets.
Prisme à base pentagonale

- Faces : cinq faces latérales et deux bases = sept faces.
- Sommets : cinq sommets à chaque base.
- Arêtes : cinq arêtes qui relient les deux bases, et cinq arêtes à chaque base.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 44.
CONNAISSANCE : PYRAMIDE
Une pyramide a seulement une base, au moins quatre faces et au moins quatre sommets. Le sommet commun est la rencontre de toutes les faces triangulaires opposées à la base. Il faut tenir compte qu’on doit inclure ce sommet dans le dénombrement des sommets. Dans une pyramide, plus le nombre de côtés de la base augmente, plus la pyramide ressemble à un cône.
Propriétés suffisantes d’une pyramide
Polyèdre dont la base est un polygone et dont les faces latérales sont triangulaires et se rencontrent à un sommet.
La base de la pyramide détermine son nom.
- Triangle : pyramide à base triangulaire
- Carré : pyramide à base carrée
- Rectangle : pyramide à base rectangulaire
- Pentagone : pyramide à base pentagonale
- Hexagone : pyramide à base hexagonale
- Octogone : pyramide à base octogonale
- Ennéagone : pyramide à base ennéagonale
- Décagone : pyramide à base décagonale
Les faces latérales d’une pyramide à base carrée sont toutes des triangles isocèles congruents. Toutefois, les faces latérales d’une pyramide à base carrée oblique ne sont pas nécessairement congrues ni des triangles isocèles.
En examinant le nombre de côtés de la base d’une pyramide, les élèves peuvent en prédire le nombre de faces, d’arêtes et de sommets.
Pyramide à base pentagonale

Faces : une base et cinq faces triangulaires.
Sommets : six sommets.
Arêtes : cinq arêtes à la base et cinq arêtes qui se rencontrent à un sommet commun, donc 10 arêtes.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 44-45.
CONNAISSANCE : FACES DE PRISMES ET DE PYRAMIDES
En explorant et en manipulant des prismes et des pyramides, ainsi qu’en créant ou en utilisant leur développement, les élèves auront l’occasion de découvrir les propriétés ayant un lien avec leurs faces.
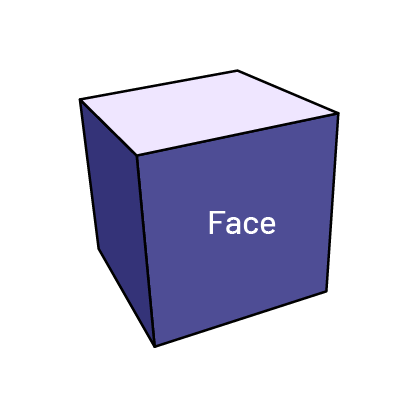
Face
Chacun des côtés qui forment un polyèdre (prismes et pyramides).
- Les faces des polyèdres sont toujours des polygones.
- Elles sont délimitées par des arêtes.
Cube
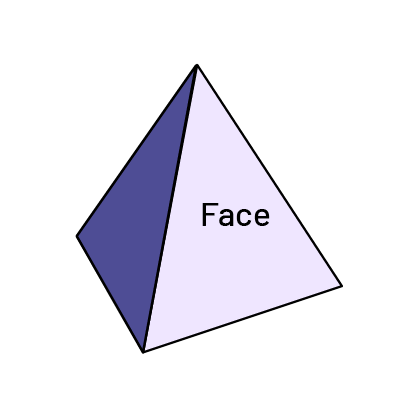
Pyramide à base carrée
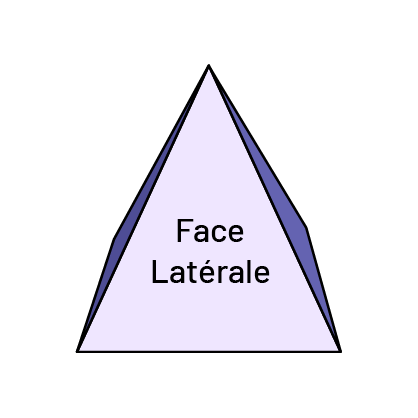
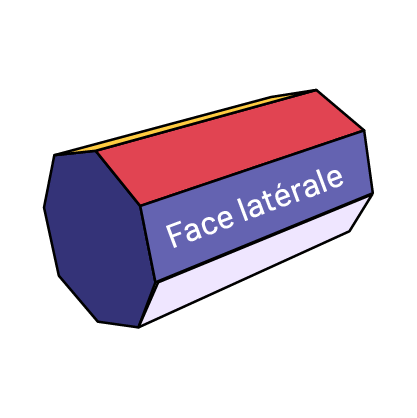
Face latérale
Dans un prisme ou une pyramide, une face latérale est une face qui ne joue pas le rôle de base.
- Les faces latérales des pyramides sont toujours des triangles.
- Les faces latérales des prismes sont généralement des rectangles ou des parallélogrammes.
Pyramide à base carrée
Pyramide à base octogonale
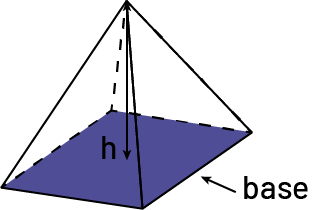
Base
Dans un prisme ou une pyramide, la base est la face à partir de laquelle on mesure la hauteur du prisme ou de la pyramide.
- Les deux bases des prismes et celle des pyramides sont toujours des polygones.
Pyramide à base carrée
Source : L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).
CONNAISSANCE : DÉVELOPPEMENT DE SOLIDES
Les développements de solides permettent de visualiser les figures planes qui composent les faces de prismes et de pyramides.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
La visualisation spatiale est un type particulier de raisonnement spatial qui implique l’utilisation de notre imagination pour « générer, mémoriser, extraire et transformer des images visuelles bien structurées » (Lohman, 1996, p. 98). Explorer les développements de solides permet aux élèves de la développer.

Un développement est une représentation en deux dimensions d’une forme en trois dimensions qu’on peut plier et recréer.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 48.
Pour visualiser le développement d’un prisme ou d’une pyramide, il faut pouvoir reconnaître le nombre et le type de polygones formant ses faces. Il faut également comprendre la façon dont les dimensions du prisme ou de la pyramide se rapportent aux dimensions des différentes faces. L’aptitude de visualiser un développement est utile pour déterminer l’aire totale.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Voici quelques exemples de développements de prismes et de pyramides.
Prisme à base triangulaire
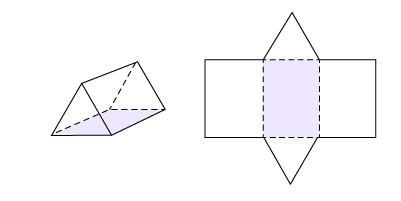
Prisme à base trapézoïdale

Pyramide à base triangulaire

Pyramide à base trapézoïdale
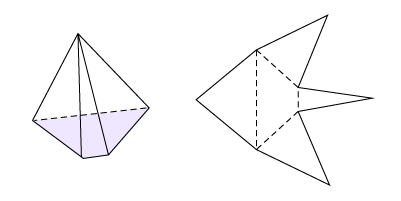
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
