La vue d'ensemble

At a Glance...

The Guides for Effective Instruction in Mathematics Revised

FrançaisEnglish

E2.5 Create and use nets to demonstrate the relationship between the faces of prisms and pyramids and their surface areas.

Skill: Determining the Relationship between the Area of Faces and the Surface Area

The surface area is the total area of the surface of a three-dimensional object.

Area is additive: partial areas can be added together to find a whole area. Finding the surface area of a prism or pyramid is an application of the property of additivity.

Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.

Additivity

The student who understands this concept realizes that the area of a shape is equal to the sum of each of the areas of its parts; similarly, the surface area of a three-dimensional object is equal to the sum of each of the areas of its faces.

Source: translated from Fiche de la 4e à la 6e année, Attribut aire, p. 3.

Knowledge: Prism

The lateral faces or sides, as opposed to top or bottom, of a prism are rectangles or parallelograms. It has at least six vertices and at least five faces. The right prism's sides are rectangles and are perpendicular to its base. The oblique prism's sides are parallelograms and are not perpendicular to its base.

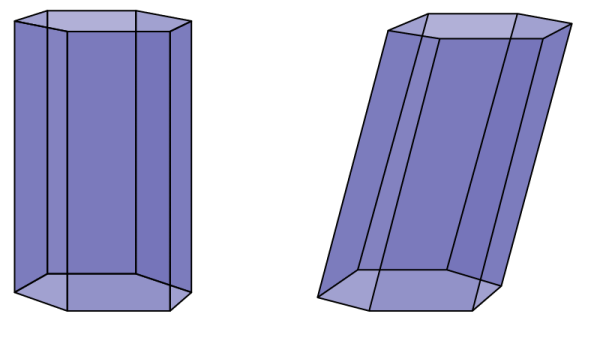
There are two three-dimensional prisms whose bases are hexagons. The first is upright while the second is oblique.

As the number of sides of the base increases, the prism looks more and more like a cylinder.

There is a three-dimensional prism placed on its side.

Sufficient Properties of a Prism

A polyhedron with two parallel and congruent polygonal bases.

The shape of the base of the prism determines its name.

  • Triangle-based prism: prism with triangular base
  • Square-based prism: prism with square base
  • Rectangle-based prism: prism with rectangular base
  • Pentagon-based prism: prism with pentagonal base
  • Hexagon-based prism: prism with hexagonal base
  • Octagon-based prism: prism with octagonal base
  • Nonagon-based prism: prism with an nonagonal base
  • Decagon-based prism: prism with a decagonal base

Examining the number of sides of the base of a prism can help students predict the number of faces, edges, and vertices.

Pentagon-Based Prism

Here is a crystal blue pentagonal prism.
  • Faces: five lateral faces and two bases = seven faces.
  • Vertices: five vertices for each base, so 10 vertices.
  • Edges: five edges that connect the two bases, and five edges at each base, so 15 edges.

Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Géométrie et sens de l'espace, Document d'appui, Fascicule 1, p. 44.

Knowledge: Pyramid

A pyramid has only one base, at least four sides and at least four vertices. The common vertex, known as the apex, is where all the triangular faces intersect. It is opposite the base. This vertex must be included in the counting of the vertices. As the number of sides of the base increases, the more the pyramid looks like a cone.

Sufficient Properties of a Pyramid

Polyhedron whose base is a polygon and whose triangular lateral faces meet at a common vertex called apex.

The base determines the name of the pyramid.

  • Triangle-based pyramid: pyramid with triangular base
  • Square-based pyramid: pyramid with square base
  • Rectangle-based pyramid: pyramid with a rectangular base
  • Pentagon-based pyramid: pyramid with a pentagonal base
  • Hexagon-based pyramid: pyramid with hexagonal base
  • Octagon-based pyramid: pyramid with an octagonal base
  • Nonagon-based pyramid: pyramid with an nanagonal base
  • Decagon-based pyramid: pyramid with a decagonal base

The side faces of a right square-based pyramid are all congruent isosceles triangles; however, the side faces of an oblique square-based pyramid are not necessarily congruent or isosceles triangles.

By examining the number of sides in the base of a pyramid, students can predict the number of faces, edges and vertices

Pentagon-Based Pyramid

Pyramid with a pentagonal base.
  • Faces: one base and five triangular faces.
  • Vertices: six vertices.
  • Edges: five edges at the base and five edges that meet at a common vertex, so 10 edges.

Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Géométrie et sens de l'espace, Document d'appui, Fascicule 1, p. 44-45.

Knowledge: Faces of Prisms and Pyramids

By exploring and manipulating prisms and pyramids, as well as creating or using their nets, students will have the opportunity to discover properties related to their faces.

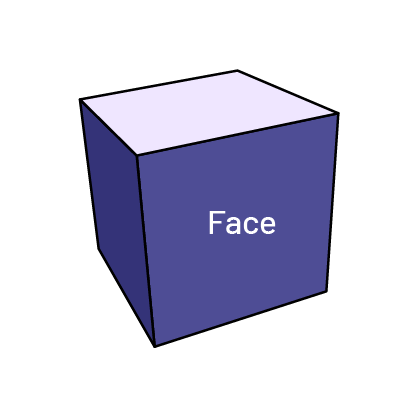
Face

Each of the sides that form a polyhedron (prisms and pyramids).

  • The faces of polyhedra are always polygons.
  • They are delineated by edges.

Cube

There is a cube, which on one side is written: face.

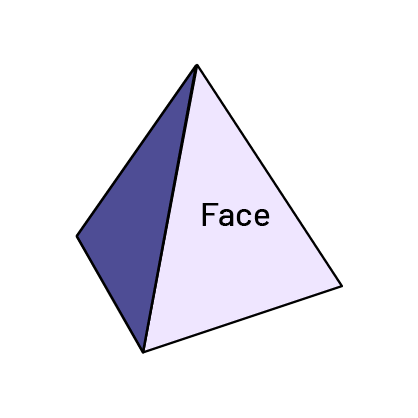
Square-Based Pyramid

There is a pyramid with a square base, which on one side is written: face.

Lateral Face

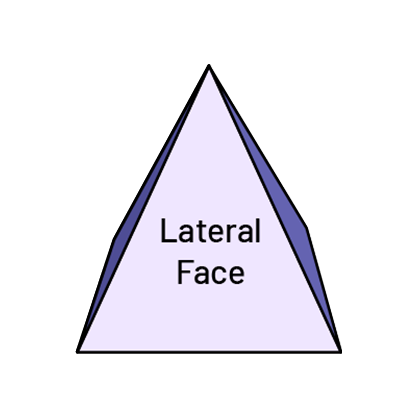
In a prism or pyramid, a lateral face is a face that does not act as a base.

  • The lateral faces of a pyramid are always triangles.
  • The lateral faces of prisms are usually rectangles.

Square-Based Pyramid

There is a pyramid with a square base, which is seen from the front. On the front facing side is written: lateral face.

Octagon-Based Prism

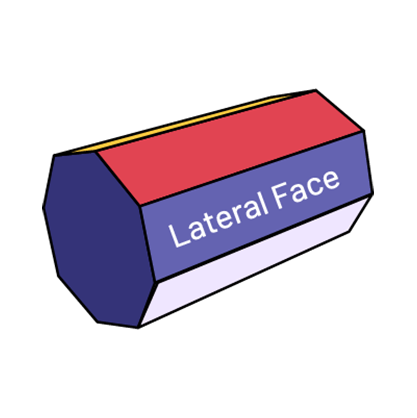
There is a prism with an octagonal base placed on its side. On one of the sides is written: lateral face.

Base

In a prism or pyramid, the base is the face from which the height of the prism or pyramid is measured.

  • The two bases of a prism and the single base of a pyramid are always polygons.

Square-Based Pyramid

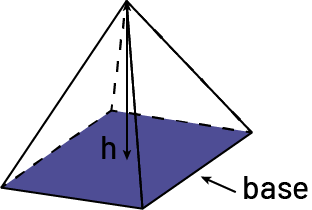
The base of a pyramid with a square base.

Source: translated from L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).

Knowledge: Net of Three-Dimensional Objects

Nets make it possible to visualize the two-dimensional shapes that make up the faces of prisms and pyramids.

Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.

Spatial visualization is a particular type of spatial reasoning that involves using our imaginations to ”generate, remember, retrieve, and transform well-structured visual images“ (Lohman, 1996, p. 98). Exploring nets of three-dimensional objects supports students to develop spatial visualization.

A spatial visualization of the development of a cube. In red, the solid is represented.

A net is a two-dimensional representation of a three-dimensional object which can be folded to create the object.

Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Géométrie et sens de l'espace, Document d'appui, Fascicule 1, p. 48.

To visualize the net of a prism or pyramid, one must be able to identify the number and type of polygons forming its faces. One must also understand how the dimensions of the prism or pyramid relate to the dimensions of the individual faces. The ability to visualize a net is useful in determining the surface area of a polyhedron.

Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.

Here are some examples of nets for prisms and pyramids.

Triangle-Based Prism

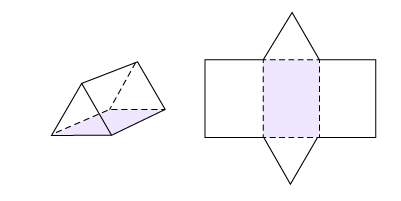
A pyramid with a triangular base and the spatial visualization of its development.

Trapezoid-Based Prism

A prism with a trapezoid base and the spatial visualization of its development.

Triangle-Based Pyramid

Pyramid with a triangular base and the spatial visualization of its development.

Trapezoid-Based Pyramid

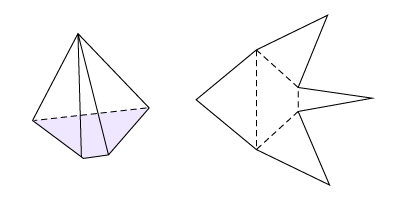
Pyramid with a trapezoidal base and the visualization of its development.

Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.