E2.6 Déterminer l’aire totale de prismes et de pyramides en calculant les aires de chaque face et en les additionnant.
HABILETÉ : DÉTERMINER L’AIRE TOTALE DE PRISMES ET DE PYRAMIDES
Les faces reliant les bases d’un prisme sont constituées de rectangles ou de parallélogrammes.
Les faces reliant la base d’une pyramide sont constituées de triangles.
L’aire de ces faces peut être déterminée au moyen de la formule d’aire d’un rectangle ou d’un parallélogramme (b × h) ou à celle d’un triangle \(\frac{1}{2} b \times h\).
Exemple
Déterminer l’aire totale d’une pyramide à base rectangulaire
Additionner les aires des cinq faces.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
On peut utiliser l’aire d’un solide pour déterminer, par exemple, la plus petite quantité de matériel qui est nécessaire pour le couvrir, ou encore la quantité de peinture qui est nécessaire pour le peindre. L’aire se mesure en unités carrées, comme des centimètres carrés ou des mètres carrés.
Le fait de connaître certaines relations entre les faces du solide permet de réduire le nombre de calculs à effectuer pour déterminer son aire. Par exemple, si on a le prisme à base rectangulaire ci-dessous, les six faces ne sont pas identiques.
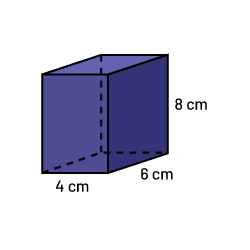Image Un prisme à base rectangulaire. Le long d’un des côtés est écrit: huit centimètres. Le long du
côté le plus court de la base est écrit: quatre centimètres; le long du côté le plus long de la base est écrit: six
centimètres.
On a plutôt trois paires de faces identiques :
- deux faces (devant et derrière) ont une aire de 32 cm2 (4 × 8) chacune;
- deux faces (sur les côtés) ont une aire de 48 cm2 (8 × 6) chacune;
- deux faces (en haut et en bas) ont une aire de 24 cm2 (4 × 6) chacune. Ainsi, l’aire totale sera égale à 208 cm2 (2 × 32 + 2 × 48 + 2 × 24).
Une façon de visualiser l’aire totale d’un solide consiste à utiliser son développement. Prenons, par exemple, le développement d’un prisme à base trapézoïdale.
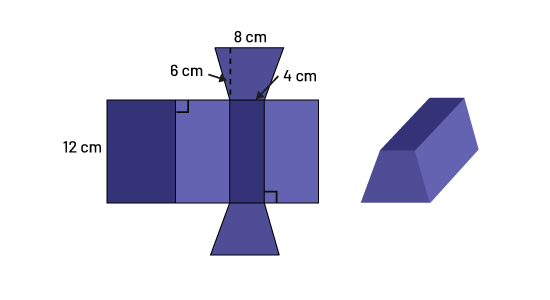Image Prisme à base trapézoïdale et son développement. La première
est une figure plate composé de quatre triangles et deux trapézoïdes. Le long d’un des côtés du trapézoïde est écrit:
huit centimètres; de l’autre côté est écrit: quatre centimètres. À côté d’une ligne pointillé allant d’un des sommets
à la base est écrit: six centimètres. Le long d’un des côtés d’un rectangle est écrit: 12 centimètres.
Afin de déterminer l’aire du prisme, il suffit d’additionner les aires des six figures planes qui composent son développement.
Les deux trapèzes ont chacun une aire de 36 cm2.
Afin de déterminer l’aire des quatre rectangles, on note que chacun a une hauteur de 12 cm et une largeur qui correspond à la mesure du côté du trapèze auquel il se rattache.
Ainsi, un rectangle a une largeur de 8 cm, un autre a une largeur de 4 cm, et les deux autres ont une largeur qui correspond à la mesure des côtés non parallèles du trapèze.
Par la suite, on fait la somme des aires des six figures du prisme.
On suit la même démarche pour trouver l’aire totale de pyramides.
Source : Réduction des écarts de rendement, 9e année, p. 19-20.