E2.6 Determine the surface areas of prisms and pyramids by calculating the areas of their two-dimensional faces and adding them together.
Skill: Determining the Surface Area of Prisms and Pyramids
The faces connecting the bases of a prism are rectangles or parallelograms.
The faces connecting the base of a pyramid are triangles.
The area of these faces can be determined using the area formula for a rectangle or parallelogram (\(\ b \times h\) ) or that of a triangle (\(\frac{1}{2} b \times h\) ).
Example
Determine the surface area of a rectangle-based pyramid.
Add the areas of the five faces.
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
The area of a three-dimensional object can be used to determine, for example, the smallest amount of material that is needed to cover it, or the amount of paint that is needed to paint it. Area is measured in square units, such as square centimetres or square metres.
Knowing some of the relationships between the faces of the three-dimensional object reduces the number of calculations needed to determine its surface area. For example, if we have the rectangle-based prism below, the six faces are not identical.
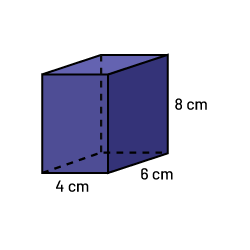Image A prism with a rectangular base. Along one of the sides is written: eight centimeters. Along the shortest side is written: four centimeters along the longest side of the base is written: six centimeters.
Instead, we have three pairs of identical faces:
- two faces (front and back) have an area of 32 cm2 (4 × 8) each;
- two faces (on the sides) have an area of 48 cm2 (8 × 6) each;
- two faces (top and bottom) have an area of 24 cm2 (4 × 6) each, so the surface area will be 208 cm2 (2 × 32 + 2 × 48 + 2 × 24).
One way to visualize the surface area of a three-dimensional object is to use its net. Take, for example, the net of a trapezoid-based prism.
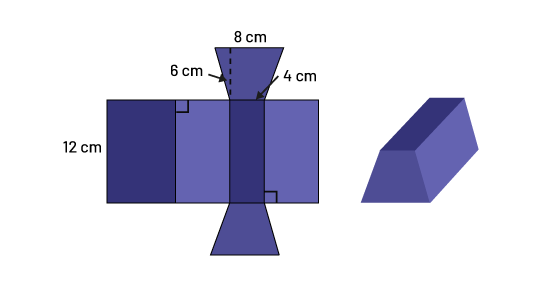Image a prism with a trapezoidal base and its development. The first is a flat figure composed of four triangles and two trapezoids. Along one of the sides of the trapezoids is written: eight centimeters; along the other side is written: four centimeters. Next to a dotted line along one of the peaks at the base is written: six centimeters. Along one of the sides of a rectangle is written 12 centimeters.
To determine the surface area of the prism, simply add the areas of the six faces that make up its net.
The two trapezoids each have an area of 36 cm2.
To determine the area of the four rectangles, note that each has a height of 12 cm and a width that corresponds to the measure of the side of the trapezoid to which it is attached.
Thus, one rectangle has a width of 8 cm, another has a width of 4 cm, and the other two have a width that corresponds to the measurement of the non-parallel sides of the trapezoid of 6.32 cm.
Thereafter, we calculate the sum of the areas of the six shapes of the prism.
We follow the same approach to find the surface area of pyramids.
Source: translated from Réduction des écarts de rendement, 9e année, p. 19-20.