La vue d'ensemble

À vue d'oeil...

Un remaniement des guides d'enseignement efficace en mathématiques

FrançaisEnglish

E2.2 Résoudre des problèmes associés au périmètre, à l’aire et au volume qui requièrent la conversion d’une unité de mesure métrique en une autre.

ACTIVITÉ 1 : PROBLÈMES D’AIRE ET DE VOLUME NÉCESSITANT DES CONVERSIONS D’UNITÉS DE MESURE

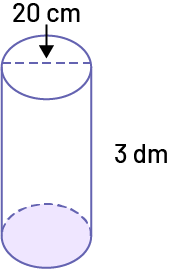
Un cylindre dont le diamètre de la base est de 20 centimètres et la hauteur est de 3 décimètres.

Tu désires envelopper ce cylindre dans du papier d’emballage pour éviter qu’il ne se brise. Quelle est l’aire totale qui doit être couverte par ce papier?

  • Quel est le volume du cylindre?
  • Quelle est la meilleure unité de mesure pour indiquer le volume? Pourquoi?

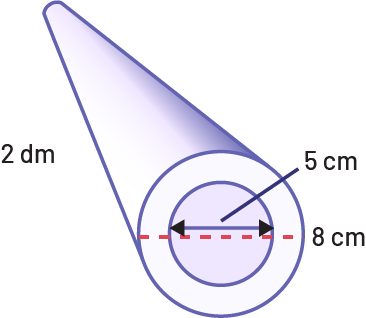
Un tuyau mesurant 2 dm de long a un diamètre extérieur de 8 cm et un diamètre intérieur de 5 cm. Quel volume de matériau faut-il pour le fabriquer? Montre ton travail.

Selon toi, quelle est la meilleure unité de mesure pour indiquer le volume?

Un tuyau dont le diamètre de l’espace vide intérieur a un diamètre de 5 centimètres., le diamètre total du tuyau est de 8 centimètres. La hauteur du tuyau est de 2 décimètres.

Source : Réduction des écarts de rendement, 9e année, p. 16.

ACTIVITÉ 2 : PROBLÈME DE PÉRIMÈTRE, D’AIRE ET DE VOLUME NÉCESSITANT DES CONVERSIONS D’UNITÉS DE MESURE

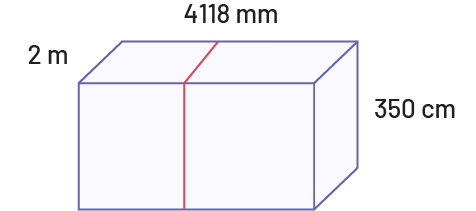
Une ficelle rouge fait le tour d’un prisme rectangulaire., la mesure est 4118 millimètres. Le côté du prisme mesure 2 mètres et sa hauteur est de 350 centimètres.
  • Quelle est la longueur de ficelle nécessaire pour entourer la boîte sur sa longueur?
  • Quel est le volume de ce prisme?
  • Si ce prisme est sur une table, quelle est l’aire totale des surfaces qui peuvent être vues?

ACTIVITÉ 3 : Quitte ou double

Former des équipes de deux, puis leur remettre un cube de un centimètre cube.

Leur demander de déterminer ses dimensions (longueur : 1 cm; largeur : 1 cm; hauteur : 1 cm), l’aire d’une face du cube (1 cm2), l’aire totale du cube (6 cm2) et son volume (1 cm3).

Inviter ensuite les élèves à déterminer les dimensions d’un prisme qui aurait le double de ce volume et à le montrer en utilisant le matériel de leur choix (par exemple, feuilles de papier quadrillé, cubes, dessin).

Circuler et observer les réponses obtenues et les stratégies utilisées afin de choisir de façon stratégique les équipes qui seront invitées à faire une présentation lors de l’échange mathématique.

Demander aux équipes choisies de présenter leur réponse et de l’expliquer. S’assurer que les présentations permettent aux élèves de comprendre :

• que pour doubler le volume, il suffit de doubler une seule des trois dimensions du cube (par exemple, 1 cm sur 1 cm sur 2 cm);

• que si on double chacune des trois dimensions (par exemple, 2 cm sur 2 cm sur 2 cm), le volume sera 8 fois plus grand.

Analyse approfondie (conversion d’unités de mesure, lien entre unités linéaires, de surface et de volume)

Modifier les arêtes du cube afin de questionner les élèves sur les changements d’aire et du volume du cube.

  • Qu’arrivera-t-il à l’aire d’une face du cube si je double la longueur de toutes les arêtes?
  • Qu’arrivera-t-il à l’aire totale du cube si je double la longueur de toutes les arêtes?
  • Qu’arrivera-t-il au volume du cube si je double la longueur de toutes les arêtes?
  • Compare les changements de l’aire avec ceux du volume. Que remarques-tu?
  • Si je double de nouveau la longueur des arêtes du cube (4 cm sur 4 cm sur 4 cm = quadruple), qu’arrivera-t-il à l’aire d’une face, l’aire totale du cube et au volume du cube?
  • Y a-t-il une façon de prédire l’aire d’une face, l’aire totale ou le volume d’un cube? Explique ta réponse.

Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 170.