La vue d'ensemble

At a Glance...

The Guides for Effective Instruction in Mathematics Revised

FrançaisEnglish

E2.2 Solve problems involving perimeter, area, and volume that require converting from one metric unit of measurement to another.

Activity 1: Area and Volume Problems Requiring Unit Conversions

A cylinder whose base diameter is 20 centimeters and the height is 3 decimeters.

A) You want to wrap this cylinder in wrapping paper to prevent it from breaking. What is the surface area that should be covered by this paper?

  • What is the volume of the cylinder?
  • What is the best unit of measurement to indicate volume? What is the reason for this?

A pipe measuring 2 dm long has an outside diameter of 8 cm and an inside diameter of 5 cm. How much material is needed to wrap it? Show your work.

What do you think is the best unit of measurement to indicate volume?

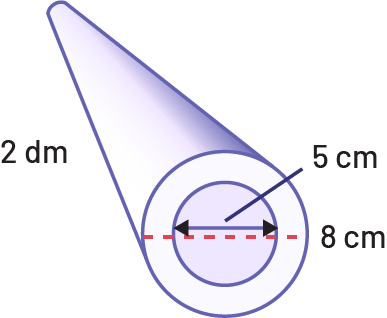
A pipe whose diameter of the inner empty space has a diameter of 5 centimeters., the total diameter of the pipe is 8 centimeters. The height of the pipe is 2 decimeters.

Source: translated from Réduction des écarts de rendement, 9e année, p. 16.

Activity 2: Perimeter, Area and Volume Problems Requiring Unit Conversions

A red string goes around a rectangular prism., the measurement is 4118 millimeters. The side of the prism measures 2 meters and its height is 350 centimeters.
  • How much string is needed to wrap around the length of the box?
  • What is the volume of this prism?
  • If this prism is on a table, what is the total area of the surfaces that can be seen?

Activity 3: Double or Nothing

Form teams of two, then give them a one-centimetre cube.

Ask them to determine its dimensions (length: 1 cm; width: 1 cm; height: 1 cm), the area of one face of the cube (1 cm2), the surface area of the cube (6 cm2) and its volume (1 cm3).

Then invite students to determine the dimensions of a prism that would have twice that volume and show it using materials of their choice (for example, sheets of graph paper, cubes, drawing).

Circulate and observe the responses and strategies used to strategically select the teams that will be invited to present at the math exchange.

Ask the selected teams to present their answer and explain it. Ensure that the presentations allow students to understand:

• that to double the volume, it is enough to double only one of the three dimensions of the cube (for example, 1 cm by 1 cm by 2 cm);

• that if we double each of the three dimensions (for example, 2 cm by 2 cm by 2 cm), the volume will be 8 times larger.

In-depth analysis (unit of measure conversion, link between linear, surface and volume units)

Modify the edges of the cube to ask students about changes in the area and volume of the cube.

  • What will happen to the area of one face of the cube if I double the length of all the edges?
  • What will happen to the total area of the cube if I double the length of all the edges?
  • What will happen to the volume of the cube if I double the length of all the edges?
  • Compare the changes in area with those in volume. What do you notice?
  • If I double the length of the edges of the cube again (4 cm by 4 cm by 4 cm = quadruple), what will happen to the area of one face, the surface area of the cube and the volume of the cube?
  • Is there a way to predict the area of a face, the surface area or the volume of a cube? Explain your answer.

Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Mesure, p. 170.