E1.1 Décrire et classer des cylindres, des pyramides et des prismes en fonction de leurs propriétés géométriques, y compris la symétrie de rotation et le plan de symétrie.
HABILETÉ : DÉCRIRE DES FIGURES GÉOMÉTRIQUES SELON LEURS PROPRIÉTÉS, Y COMPRIS LA SYMÉTRIE DE ROTATION ET LE PLAN DE SYMÉTRIE
Afin de pouvoir classer des figures géométriques, l’élève doit d’abord être capable de décrire les figures de base. Pour ce faire, il est essentiel de connaître le vocabulaire et de comprendre ce que chacune des propriétés signifie. Plusieurs de ces caractéristiques ont été vues dès le cycle primaire, ce qui ne signifie pas pour autant que les concepts associés à celles-ci ont été maîtrisés. Il est donc important de les revoir, particulièrement la symétrie rotationnelle abordée en 6e année.
Une fois les concepts maîtrisés, il est plus facile d’ajouter de nouveaux concepts sur cette base mathématique, comme le plan de symétrie.
Il est avantageux pour l’élève de produire des listes de propriétés et d’utiliser ces propriétés pour formuler des arguments géométriques afin de développer le sens de l’espace. Les listes de propriétés minimales ou suffisantes énoncent le plus petit nombre de propriétés nécessaires pour reconnaître une classe de formes géométriques (par exemple, si un prisme n’a qu’un seul plan de symétrie, il s’agit alors d’un prisme oblique).
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
CONNAISSANCE : PROPRIÉTÉS GÉOMÉTRIQUES
Une propriété géométrique est un attribut qui aide à définir une classe de solides, les trois grandes classes étant les cylindres, les pyramides et les prismes. Parmi ces attributs utilisés pour les distinguer, il y a :
- la forme de la base ou des bases;
- le nombre de bases;
- le nombre d’arêtes et de sommets;
- le fait d’être symétrique ou non;
- le fait que les faces soient ou non perpendiculaires aux bases.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
Voici des mots de vocabulaire qui permettent de décrire et de classer des cylindres, des pyramides et des prismes
- Base : La base ou les bases d’un prisme ou d’une pyramide sont des polygones qui donnent le nom au solide.
- Face : Chacun des côtés qui forment un polyèdre (prismes et pyramides). Les faces de ces solides sont toujours des polygones. Elles sont délimitées par des arêtes.
- Face latérale : Sur un prisme ou une pyramide, une face latérale est une face qui ne joue pas le rôle de base.
- Surface : Sur les corps ronds, les faces courbes sont nommées surface.
Note : Il est important de signaler que les termes face et surface sont parfois employés différemment selon les écoles de pensée ou les ressources utilisées.
- Arêtes : L’arête est un segment qui forme l’intersection de deux faces d’une pyramide ou d’un prisme.
- Sommet : Le sommet est le point de rencontre d’au moins deux arêtes d’une pyramide ou d’un prisme.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 43.
Ainsi, connaître les propriétés nécessaires d’une figure géométrique permet de décrire l’ensemble des propriétés de cette figure, tandis que connaître les propriétés suffisantes d’une figure permet de déterminer les propriétés clés qui sont essentielles pour décrire une figure géométrique et la distinguer des autres. Lorsqu’on connaît les propriétés suffisantes, on sait exactement la figure dont il est question.
Avant de pouvoir classer des figures géométriques, il est important de connaître leurs propriétés et de les décrire.
|
Propriété selon la classe de solide (figure tridimensionnelle) |
Cylindre |
Pyramide |
Prisme |
|
La forme de la base ou des bases |
Formes qui peuvent varier. (Note : Si les bases sont des polygones, ce sont des prismes.) |
Polygone qui peut varier. |
Polygones qui peuvent varier. |
|
Nombre de bases avec leurs propriétés |
Deux bases congruentes parallèles en ses extrémités. |
Une base sur laquelle reposent des triangles qui se rencontrent à l’apex. |
Deux bases congruentes parallèles, les autres faces étant des rectangles ou des parallélogrammes. |
|
Type(s) de symétrie |
Symétrie de translation, c’est-à-dire une base est l’image congruente d’une autre base ayant subi une translation. (Note : Cylindres droits circulaires : plan de symétrie et symétrie de rotation.) Peuvent avoir une symétrie de rotation ou de réflexion. |
Symétrie de rotation ou de réflexion entre les triangles. |
Symétrie de translation, c’est-à-dire une base est l’image congruente d’une autre base ayant subi une translation. Peuvent avoir une symétrie de rotation ou de réflexion. |
|
Lignes droites et faces par rapport à la base ou aux bases |
Les cylindres droits sont formés de lignes droites parallèles, perpendiculaires aux bases. Sinon, les cylindres sont obliques. |
Pyramides droites dont l’apex de la pyramide se situe au-dessus du centre de la base. Sinon, les pyramides sont obliques. |
Les prismes droits sont formés de lignes droites parallèles, perpendiculaires aux bases. Sinon, les prismes sont obliques. |
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
Voici un exemple de description de solides selon ses propriétés géométriques.
|
Solide |
Nom du solide et leurs propriétés géométriques |
 |
Pyramide droite à base triangulaire ou tétraèdre
|
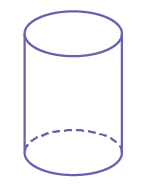 |
Cylindre droit à base circulaire
|
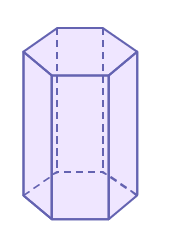 |
Cylindre ou prisme à base hexagonale
|
 |
Cube
|
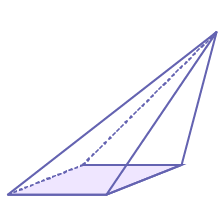 |
Pyramide oblique à base rectangulaire
|
 |
Prisme oblique à base rectangulaire
|
 |
Cylindre non circulaire
|
Source : En avant, les maths!, 7e année, CM, Sens de l'espace, p. 5-7.
HABILETÉ : CLASSER DES FIGURES GÉOMÉTRIQUES SELON LEURS PROPRIÉTÉS, Y COMPRIS LA SYMÉTRIE DE ROTATION ET LE PLAN DE SYMÉTRIE
L’analyse des propriétés des figures planes et des solides permet de développer les habiletés de la pensée liées au raisonnement déductif informel.
Les élèves peuvent formuler des hypothèses au sujet des propriétés géométriques et des liens entre elles à mesure que leur compréhension des formes géométriques évolue. En utilisant des dessins, du matériel de manipulation et des logiciels pour développer et vérifier cette compréhension, elles et ils acquièrent aussi l’habileté à articuler des arguments mathématiques clairs pour expliquer la raison pour laquelle une relation géométrique est vraie. (National Council of Teachers of Mathematics, 2003, p. 165-166, traduction libre)
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 31.
La mise en évidence des relations d’inclusion et d’exclusion aide les élèves à comparer, à évaluer et à analyser les concepts à l’étude. Cela permet donc une conceptualisation et un apprentissage plus profond de la part des élèves.
Voici un exemple d’inclusion : tous les prismes sont délimités par deux polygones identiques et parallèles, mais ce ne sont pas toutes les figures ayant deux polygones identiques et parallèles en leurs extrémités qui sont des prismes; tous les prismes sont des cylindres, mais ce ne sont pas tous les cylindres qui sont des prismes.
Voici un exemple d’exclusion : les prismes et les cylindres ont deux bases identiques et parallèles, contrairement aux pyramides qui n’en ont qu’une seule.
Le diagramme de Venn et le diagramme d’Euler sont des outils de choix pour distinguer les similitudes et les différences entre les solides.
Exemple
Dans l’exemple ci-dessous, il faut classer les solides selon s’ils ont au moins une face qui est un quadrilatère et selon s’ils ont une symétrie de rotation. Le nom des solides est donné. L’élève aurait pu devoir indiquer les noms après avoir pris connaissance des caractéristiques des différentes figures (vocabulaire).

Nom des solides
- Cube
- Prisme à base triangulaire
- Cylindre
- Prisme à base pentagonale
- Pyramide à base triangulaire
- Sphère
- Pyramide à base rectangulaire
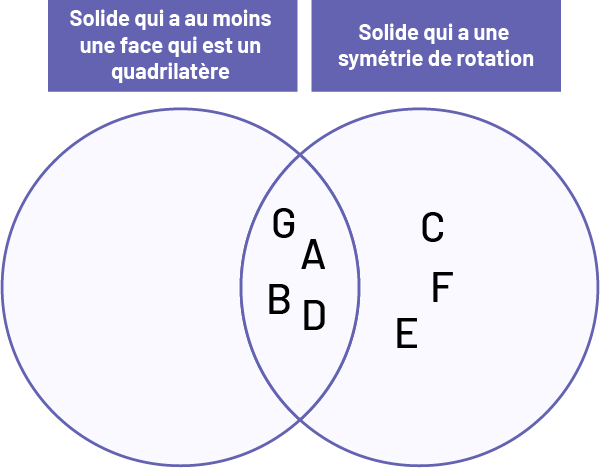
Voici le résultat de cette classification.
 image
Schéma de classification formé de deux cercles qui se chevauchent. Titre du premier cercle « solide qui a au moins une
face est un quadrilatère ». Titre du second cercle : « solide qui a une symétrie de rotation ». Dans ce cercle
uniquement on retrouve les solides : « C », « F », « E ». Dans l’espace de chevauchement des deux cercles, on
retrouve : « A », « B », « D », « G ».
image
Schéma de classification formé de deux cercles qui se chevauchent. Titre du premier cercle « solide qui a au moins une
face est un quadrilatère ». Titre du second cercle : « solide qui a une symétrie de rotation ». Dans ce cercle
uniquement on retrouve les solides : « C », « F », « E ». Dans l’espace de chevauchement des deux cercles, on
retrouve : « A », « B », « D », « G ».
CONNAISSANCE : CYLINDRE
Figure tridimensionnelle comprenant deux faces parallèles et congruentes appelées bases. Les bases du cylindre peuvent être des polygones, des faces courbes fermées ou une combinaison des deux.
Note : Si la base d’un cylindre est circulaire, il s’agit d’un cylindre à base circulaire (ou cylindre circulaire). Si la base d’un cylindre est un polygone, le cylindre est également un prisme.
Exemple
 image Cylindres circulaires, par exemple : Cylindre oblique à base
circulaire, cylindre droit à base circulaire, cylindre. Cylindre non circulaire. Cylindres de type spécial, prisme
triangulaire à base rectangle, Prisme oblique à base rectangulaire.
image Cylindres circulaires, par exemple : Cylindre oblique à base
circulaire, cylindre droit à base circulaire, cylindre. Cylindre non circulaire. Cylindres de type spécial, prisme
triangulaire à base rectangle, Prisme oblique à base rectangulaire.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
CONNAISSANCE : PRISME
Figure tridimensionnelle avec deux bases parallèles et congruentes. Un prisme se distingue par la forme de ses bases (par exemple, prisme à base rectangulaire, prisme à base triangulaire, prisme à base hexagonale). Les prismes sont des cas particuliers des cylindres dont les faces sont des polygones.
Note : Les prismes peuvent être droits ou obliques selon que les lignes, y compris les arêtes, qui relient les bases sont perpendiculaires ou non aux bases.
Exemple

Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
CONNAISSANCE : PYRAMIDE
Polyèdre dont la base est un polygone et dont les faces latérales triangulaires se rencontrent en un sommet commun nommé apex.
Note : Les pyramides peuvent être droites ou obliques selon que l’apex de la pyramide se situe directement au-dessus du centre de sa base.
Exemple

Source : En avant les maths 7e année, CM, Sens de l’espace, p. 3.
CONNAISSANCE : SYMÉTRIE DE ROTATION
Propriété géométrique selon laquelle la position d’un solide coïncide avec sa position initiale après une rotation de moins de 360° autour de son centre.
Exemple
La position d’un cube coïncide avec sa position initiale après \(\frac{1}{4}\) de tour, \(\frac{1}{2}\) tour et \(\frac{3}{4}\) de tour autour du point de rotation en son centre, ce qui signifie que le cube a une symétrie de rotation.
L’ordre de symétrie de rotation est le nombre de fois qu’une figure géométrique peut pivoter en conservant le même aspect avant une rotation complète. Ci-dessous, la vue de haut d’un cube après une rotation de 90° autour d’un axe de rotation; cet axe a un ordre de 4 (4 × 90° = 360°).
 image Un
cube est placé sur un axe. Une étoile est visible sur la vue d’en haut à un des coins. L’étoile change de position
pour tous les quarts de tour qu’effectue le cube. Donc en se basant sur sa position de départ, on peut voir, un quart
de tout, un demi-tour, un trois quart de tour.
image Un
cube est placé sur un axe. Une étoile est visible sur la vue d’en haut à un des coins. L’étoile change de position
pour tous les quarts de tour qu’effectue le cube. Donc en se basant sur sa position de départ, on peut voir, un quart
de tout, un demi-tour, un trois quart de tour.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
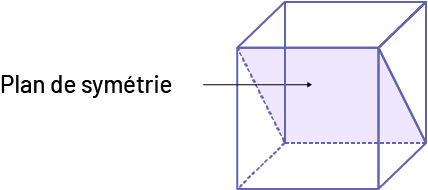
CONNAISSANCE : PLAN DE SYMÉTRIE
Plan traversant un objet tridimensionnel qui divise cet objet en deux parties, chacune étant l’image miroir de l’autre (symétrique).
Exemple
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
