E1.1Describe and classify cylinders, pyramids, and prisms according to their geometric properties, including plane and rotational symmetry.
Skill: Describing Three-Dimensional Objects According to Their Properties, Including Plane and Rotational Symmetry
In order to be able to classify three-dimensional objects, the student must first be able to describe the basic ones. To do this, it is essential to know the vocabulary and understand what each of the properties means. Several of these properties have been seen since the primary grades, but this does not mean that the concepts associated with them have been mastered. It is therefore important to review them, particularly the rotational symmetry introduced in Grade 6.
Once the concepts are mastered, it is easier to add new concepts on this solid foundation, such as the plane symmetry.
It is advantageous for the student to produce lists of properties and to use these properties to formulate geometric arguments in order to develop spatial sense. Minimum property lists identify the fewest properties needed to identify a class (for example, if a prism has only one plane of symmetry, then it is an oblique prism).
Source: adapted from The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
Knowledge: Geometric Property
A geometric property is an attribute that helps define a class of objects. Cylinders, pyramids, and prisms represent three broad categories of three-dimensional objects. There are many attributes that are used to distinguish and define sub-categories or classes of objects, including:
- the shape of the base or bases;
- the number of bases;
- the number of edges and vertices;
- whether the object is symmetrical (for example, whether it has rotational or plane symmetry);
- whether the faces are perpendicular to the bases.
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
- Base: The base or bases of a prism or pyramid are polygons that give the solid its name.
- Face: Each of the sides that form a polyhedron (prisms and pyramids). The faces of these three-dimensional objects are always polygons. They are bounded by edges.
- Lateral face: On a prism or pyramid, a face that does not act as the base.
- Surface: On non polyhedrons, the curved faces are called surfaces.
Note: It is important to note that the terms face and surface are sometimes used differently depending on the school of thought or the resources used.
- Edges: An edge is a segment that forms the intersection of two faces of a pyramid or prism.
- Vertex: The vertex is the point where at least two edges of a pyramid or prism meet.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Géométrie et sens de l'espace, Document d'appui, Fascicule 1, p. 43.
Thus, knowing the necessary properties of a geometric shape makes it possible to describe all the properties of this shape, while knowing the minimum properties of a shape makes it possible to determine the key properties that are essential to describe a geometric shape or object and to distinguish it from others. When we know the minimum properties, we know exactly the shape or object in question.
Before being able to classify three-dimensional objects, it is important to know their properties and describe them.
|
Property According to the Class of Three-Dimensional Object |
Cylinder |
Pyramid |
Prism |
|
The shape of the base or bases |
Shapes that may vary. (Note: If the bases are polygons, they are prisms.) |
Polygon that can vary. |
Polygons that can vary. |
|
Number of bases with their properties |
Two congruent and parallel bases. |
A base on which rest lateral triangular faces that meet at the apex. |
Two congruent parallel bases, the lateral faces being rectangles or parallelograms. |
|
Type(s) of symmetry |
Translational symmetry, that is a base is the congruent image of another base having undergone a translation. (Note: Straight circular cylinders: plane and rotational symmetry.) May have rotational or reflective symmetry. |
Rotational or reflective symmetry between triangles. |
Translational symmetry, that is a base is the congruent image of another base that has undergone a translation. Can have rotational or reflective symmetry. |
|
Straight lines and faces in relation to the base or bases |
Right cylinders are formed by parallel lines (elements), perpendicular to the bases. Otherwise, the cylinders are oblique. |
Right pyramids have an apex that lies directly above the center of the base. Otherwise, the pyramids are oblique. |
Right prisms are formed by parallel lines (elements), perpendicular to the bases. Otherwise, prisms are oblique. |
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
Here is an example of describing three-dimensional objects according to their geometric properties.
|
Three-Dimensional Object |
Name of the Three-Dimensional Object and Its Geometric Properties |
 |
Triangle-based right pyramid or tetrahedron
|
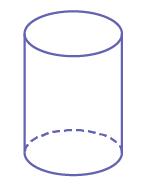 |
Right circular cylinder
|
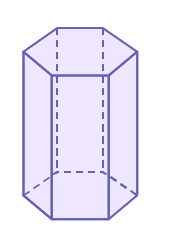 |
Hexagon-based cylinder or prism
|
 |
Cube
|
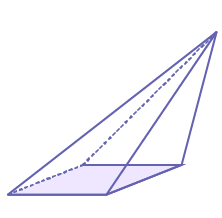 |
Oblique rectangle-based pyramid
|
 |
Oblique rectangle-based prism
|
 |
Non-circular cylinder
|
Source: translated from En avant, les maths!, 7e année, CM, Sens de l'espace, p. 5-7.
Skill: Classifying Three-Dimensional Objects According to Their Properties, Including Plane and Rotational Symmetry
Analyzing the properties of two-dimensional shapes and three-dimensional objects develops thinking skills related to informal deductive reasoning.
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 1, p. 31.
Highlighting the relationships of inclusion and exclusion helps students compare, evaluate and analyze the concepts under study. This allows for deeper conceptualization and learning on the part of the students.
An example of inclusion is that all prisms are bounded by two identical and parallel polygons, but not all objects with two identical and parallel polygons at their ends are prisms; all prisms are cylinders, but not all cylinders are prisms.
An example of an exclusion is that prisms and cylinders have two identical and parallel bases, unlike pyramids which have only one.
The Venn diagram and Euler diagram are prime tools for distinguishing similarities and differences between three-dimensional objects.
Example
In the example below, the three-dimensional objects must be classified according to whether they have at least one face that is a quadrilateral and according to whether they have rotational symmetry. The names of the three-dimensional objects are given. The student could indicate the names after having learned the characteristics of the different objects (vocabulary).

Name of the Three-Dimensional Objects
- Cube
- Triangle-based prism
- Cylinder
- Pentagon-based prism
- Triangle-based pyramid
- Sphere
- Rectangle-based pyramid
The result of this classification in a Venn diagram is below.
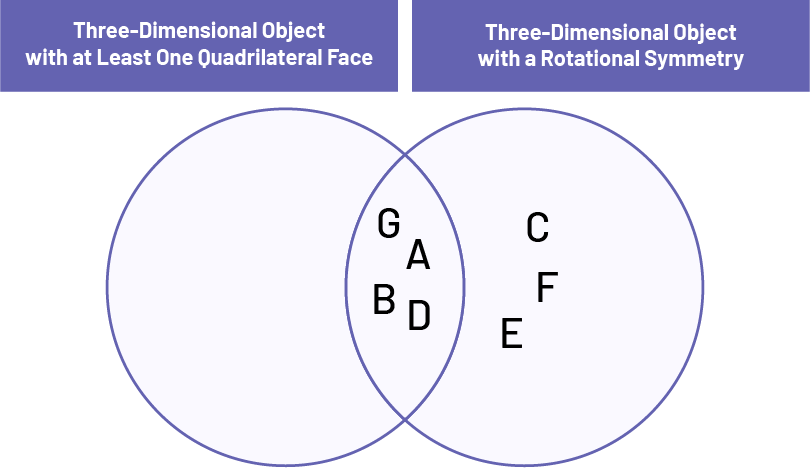 image Classification scheme formed by two overlapping circles. Title of the first circle: « solid that has at least one quadrilateral face ». Title of the second circle: « Solid that has a rotation symmetry ». In the circle only we find the solids: « C », « F », « E ». In the space where the circles overlap, we find: « A », « B », « D », « G ».
image Classification scheme formed by two overlapping circles. Title of the first circle: « solid that has at least one quadrilateral face ». Title of the second circle: « Solid that has a rotation symmetry ». In the circle only we find the solids: « C », « F », « E ». In the space where the circles overlap, we find: « A », « B », « D », « G ».
Knowledge: Cylinder
A cylinder is a three-dimensional object which has two parallel and congruent faces called bases. The bases of a cylinder may be circular, or its edges may be curved, straight, or some combination of curved and straight.
Note: If the base of a cylinder is circular, it is a circular cylinder. If the base of a cylinder is a polygon, the cylinder is also a prism.
Example
 image Circular cylinders, for example: Oblique cylinder with a circular base, straughts cylinder with a circular base, cylinder. Non-circular cylinders.Special type cylinders, triangular prism wirh rectangular base, oblique prism with rectangular base.
image Circular cylinders, for example: Oblique cylinder with a circular base, straughts cylinder with a circular base, cylinder. Non-circular cylinders.Special type cylinders, triangular prism wirh rectangular base, oblique prism with rectangular base.
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
Knowledge: Prism
Prisms are special types of cylinders, with two congruent, polygonal faces that are parallel to each other. These are the bases of the prism. A prism is named for the shape of its base. So, for example, triangle-based prisms (or, simply, triangular prisms) have two bases that are triangular, which are joined by parallelograms (including rectangles).
Note: Prisms can be right or oblique depending on whether the lines, including the edges, that connect the bases are perpendicular to the bases or not.
Example

Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
Knowledge: Pyramid
A pyramid is a three-dimensional object whose base is a polygon and whose triangular lateral faces meet at a common vertex called the apex.
Note: Pyramids can be right or oblique depending on whether the apex of the pyramid is lying directly above the center of its base.
Example

Source: translated from En avant les maths 7e année, CM, Sens de l'espace, p. 3.
Knowledge: Rotational Symmetry
A three-dimensional object has rotational symmetry if it can be turned about an axis of rotation and look the same as the original after a rotation of less than 360°.
Example
The position of a cube coincides with its initial position after \(\frac{1}{4}\ turn, \frac{1}{2}\ turn and \frac{3}{4}\) turn around the axis of rotation in its center, which means that the cube has a rotational symmetry.
The order of rotational symmetry is the number of times a geometric figure can be rotated and look the same before it has been rotated all the way around (full rotation). Pictured below is the top view of a cube rotated 90° around an axis of rotation. It has an order of rotational symmetry of 4 (4 × 90° = 360°).
 image A cube is placed on an axis. A star is visible on the top view at one of the corners.The star changes position for every quarter turn made by the cube. So based on its starting position, we can see, a quarter of a turn, a half turn, a three quarter turn.
image A cube is placed on an axis. A star is visible on the top view at one of the corners.The star changes position for every quarter turn made by the cube. So based on its starting position, we can see, a quarter of a turn, a half turn, a three quarter turn.
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
Knowledge: Plane Symmetry
A three-dimensional object has plane symmetry if it can be divided into two congruent halves that are mirror images of each other.
Example

Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
