E1.3 Effectuer des homothéties et décrire la similarité entre l’image et la figure initiale.
HABILETÉ : EFFECTUER DES HOMOTHÉTIES
Lorsqu’on effectue des homothéties, le rapport d’homothétie k détermine si on produit des images semblables qui sont plus grandes (k > 1) ou plus petites (k < 1). Ce rapport k est en fait le rapport entre la mesure d’un côté de l’image par rapport à la mesure du côté correspondant de la figure initiale.
Pour effectuer une homothétie, on multiplie les coordonnées de la figure initiale par le rapport d’homothétie. La mesure des côtés de l’image résultante sera k fois celle des côtés « correspondants de la figure initiale ».
Par exemple, les côtés d’un triangle formé par les points A(1, 1), B(4, 1) et C(1, 5) mesurent 3, 4 et 5 unités. Si on fait subir une homothétie de rapport 2 à ce triangle, les points correspondants de l’image seront A’(2, 2), B’(8, 2) et C’(2, 10), et les mesures des côtés seront 6, 8 et 10 unités.
Figure initiale → image
(x, y) → (kx, ky)
A (1, 1) → A' (2, 2)
B (4, 1) → B' (8, 2)
C (1, 5) → C' (2, 10)
Il est également possible d’effectuer cette homothétie en multipliant la mesure des côtés par deux et en s’assurant de garder la congruence de chaque angle.
HABILETÉ : DÉCRIRE LA SIMILARITÉ ENTRE L’IMAGE ET LA FIGURE INITIALE
Il est important que l’élève réalise que, contrairement aux translations, aux réflexions et aux rotations, une homothétie ne produit pas une image congruente. Cependant, la valeur des angles est conservée ainsi que le rapport entre les côtés.
Une image ayant subi une homothétie est donc semblable à la figure initiale. Dans le langage courant, une image semblable est une image qui ressemble simplement à autre chose. En mathématiques, le terme semblable a une signification très précise. Les figures semblables ont la même forme, mais des tailles différentes. Elles sont proportionnelles : leurs angles restent les mêmes, et la longueur de leurs côtés est réduite ou agrandie suivant un rapport d’homothétie constant. Si la largeur d’un rectangle ayant subi une homothétie est deux fois celle de la figure initiale, sa longueur le sera aussi.
Les applications de géométrie dynamique sont des outils recommandés pour aider les élèves à comprendre la façon dont les transformations se comportent en mouvement. Dans un environnement dynamique, le fait de repositionner le centre d’homothétie a une incidence immédiate, tout comme le fait de changer le rapport d’homothétie.
Ainsi, lorsqu’on dit que des figures sont semblables, on souligne que l’image montre de la similarité avec la figure initiale.
- Similarité. Des figures semblables sont des figures qui ont exactement la même forme, dont les mesures d’angles homologues sont équivalentes et dont les mesures des côtés homologues ont la même proportionnalité.
- Image. Figure obtenue à la suite de la transformation d’une figure initiale donnée.
- Figure initiale. Figure sur laquelle on applique une transformation géométrique.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
CONNAISSANCE : HOMOTHÉTIE
Transformation géométrique. Opération qui, à partir d’une règle donnée, consiste à faire correspondre tout point du plan à une seule image. La translation, la rotation, la réflexion et l’homothétie sont des exemples de transformations géométriques. Cette modification dans une figure a comme résultat d’en modifier la position, l’orientation ou la taille.
Homothétie. Transformation qui a pour effet d’agrandir ou de réduire une figure selon un rapport donné afin que l’image soit semblable à la figure originale.
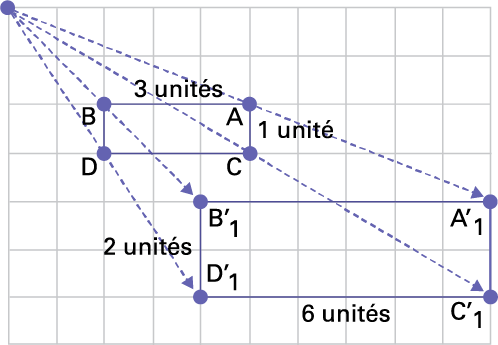
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
