E2.3 Utiliser les relations entre le rayon, le diamètre et la circonférence d’un cercle pour expliquer la formule de calcul de la circonférence d’un cercle et pour résoudre des problèmes connexes.
HABILETÉ : UTILISER LES RELATIONS ENTRE LE RAYON, LE DIAMÈTRE ET LA CIRCONFÉRENCE D’UN CERCLE POUR EXPLIQUER LA FORMULE DE CALCUL DE LA CIRCONFÉRENCE
Pour mesurer le périmètre d’un cercle, qu’on appelle circonférence (C), il est possible de placer une ficelle autour du cercle, puis de mesurer par la suite la longueur de la ficelle utilisée. Cela est plus facile que de placer un ruban à mesurer autour d’un cercle.
Il est également possible de déterminer la circonférence d’un cercle en mesurant directement son diamètre (d), puis en multipliant cette valeur par π. Le diamètre correspond à la plus grande distance de part et d’autre du cercle. Le diamètre passe automatiquement par le centre du cercle et correspond au double de la longueur de son rayon (r).
La circonférence d’un cercle est un peu plus de trois fois la longueur de son diamètre (ou un peu plus de six fois la longueur de son rayon). Ce rapport est constant et est décrit à l’aide du symbole grec π (épelé et prononcé pi). Cette relation peut être exprimée de façon symbolique par (C = πd) ou par (C = π2r).
Puisque la circonférence d’un cercle est égale à son diamètre multiplié par π : \(C = \pi d\) et que le diamètre est le double du rayon : \(d = 2r\), on écrit régulièrement la formule de la circonférence comme étant : \(C = 2 \pi r\)
Si on mesure la circonférence d’un cercle et qu’on divise cette valeur par celle de son diamètre \((\frac{C}{d})\), la réponse correspond à notre estimation de π. C’est une relation très importante, qui est utilisée dans un grand nombre de formules de mathématiques et de physique. Pi équivaut environ à 3,141 59, mais est un nombre irrationnel, ce qui signifie qu’il ne pourrait jamais être calculé de façon exacte. Il a un nombre infini de décimales et ne peut pas être représenté précisément en fraction.
Lorsque les outils utilisés pour calculer π sont peu précis, comme dans une classe de niveau intermédiaire, les valeurs obtenues correspondent souvent à 3,1, « un peu plus de trois ». Mais pour les astrophysiciennes et les astrophysiciens qui calculent la circonférence de l’univers observable, π doit être calculé avec 39 décimales.
Communément, π est arrondi à 3,14 (ou représenté, en fraction, par \(\frac{22}{7}\)). Cependant, les mathématiciennes et les mathématiciens ont calculé pi à des billions (mille milliards) de décimales à l’aide de superordinateurs.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Mesure de la longueur, le diamètre, la circonférence, le périmètre et l’aire
 Description de la vidéo
Description de la vidéo
Description à venir
CONNAISSANCE : CERCLE
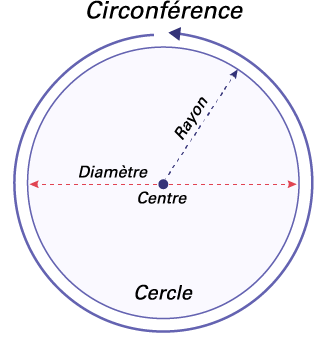
Ensemble des points d’un plan formant une courbe plane fermée dont tous les points sont à égale distance du centre.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
CONNAISSANCE : RAYON
Segment de droite reliant le centre d’un cercle à sa circonférence.
Note : Le rayon est égal à la moitié du diamètre, soit \(r = \frac{d}{2}\).
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
CONNAISSANCE : DIAMÈTRE
Le diamètre (d) d’un cercle est la distance la plus longue entre un côté d’un cercle et un autre. Le diamètre passe toujours au centre du cercle; il équivaut donc à deux rayons (r). Cette relation peut être exprimée de façon symbolique par (d = 2r) ou (r = d ÷ 2).
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
CONNAISSANCE : PI (π)
Nombre qui représente le rapport constant de la circonférence d’un cercle à son diamètre. Sa valeur est d’environ \(3\frac{1}{7}\), plus précisément de 3,141 592 653 ou de 3,14.
\(\frac{C}{d} = \pi\)
\(\pi = 3,141 59…\)
\(\pi \approx 3,14\)
\(\pi \approx 3\frac{1}{7}\)
Source : En avant, les maths!, 7e année, CM, Sens de l’espace, p. 2.
CONNAISSANCE : CIRCONFÉRENCE
Mesure de la longueur d’un cercle ou du périmètre d’un disque. La formule pour calculer la circonférence (C) d’un cercle est \(C = \pi d\) ou \(C = 2\pi r \), où d est le diamètre du cercle et r, son rayon.
Source : En avant, les maths!, 7e année, CM, Sens de l’espace, p. 2.
