E2.3 Use the relationships between the radius, diameter, and circumference of a circle to explain the formula for finding the circumference and to solve related problems.
Skill: Using the Relationships between the Radius, Diameter and Circumference of a Circle to Explain the Formula for Calculating the Circumference
To measure the perimeter of - or distance around - a circle, which is called the circumference (C), it is possible to place a string around the circle and then measure the length of the string used. This is easier than placing a tape measure around a circle.
It is also possible to determine the circumference of a circle by measuring its diameter (d) directly, and then multiplying that value by π. The diameter (d) of a circle is the longest distance from one side of a circle to another. The diameter will always pass through the centre of the circle, so it is the same as two radii (r).
The circumference of a circle is a little more than three times the length of the diameter, or a little more than six times the length of the radius. This ratio is constant and is described using the Greek symbol π (spelled pi and pronounced like pie). This relationship can be expressed symbolically as C = πd or, equivalently, as C = π2r.
Since the circumference of a circle is equal to its diameter multiplied by π: \(C = \pi d\) and the diameter is twice the radius: \(d = 2r\), the formula for the circumference is regularly written as: \(C = 2 \pi r\)
Pi (π) is equal to c/d , which is a very important relationship, used in many math and physics formulas. It is approximately equal to 3.14159, and it is an irrational number, which means that it can never be exactly calculated: its decimals never end, and it cannot be represented precisely as a fraction.
Commonly, π is approximated as 3.14 (or in fraction form as 22/7). However, some scientific applications round π to hundreds of digits, and mathematicians, using supercomputers, have calculated π to trillions of digits. For astrophysicists calculating the circumference of the observable universe, π must be calculated to 39 digits.
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
Knowledge: Circle
A two-dimensional shape with a curved side. All points on the side of a circle are equidistant from its centre.
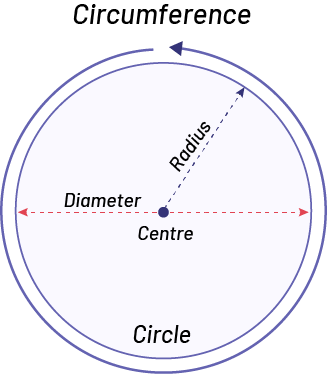image A circle where we have indicated:The radius, which goes from the center to the edge of the circle.The diameter, which starts from the edge of the circle and crosses it through the center.The circumference which is the total outline of the circle.
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
Knowledge: Radius
A line segment whose endpoints are the centre of a circle and a point on the circle. The radius is half the diameter.
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
Knowledge: Diameter
A line segment that joins two points on a circle and passes through the centre. The diameter is twice as long as the radius. This relationship can be expressed symbolically as (d =2r) or (r = d ÷ 2).
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
Knowledge: PI (π)
A number that represents the constant ratio of a circle's circumference to its diameter. Its value is approximately \(3\frac{1}{7}\), more precisely 3.141,592,653 or 3.14.
\(\frac{c}{d} = \pi\)
\(\pi\ = 3.141 59…\)
\(\pi \approx 3,14\)
\(\pi \approx 3\frac{1}{7}\)
Source: translated from En avant, les maths!, 7e année, CM, Sens de l’espace, p. 2.
Knowledge: Circumference
A measure of the length of, or distance around, a circle or the perimeter of a disk. The formula for calculating the circumference (C) of a circle is C = πd or
C = π2r, where d is the diameter of the circle and r is the radius.
Source: translated from En avant, les maths!, 7e année, CM, Sens de l’espace, p. 2.