Fondements généraux du domaine Sens de l'espace
Cycle intermédiaire
De la 1re à la 8e année, les éléments mesure et géométrie sont intégrés dans un domaine Sens de l’espace. Cela permet aux élèves de développer les habiletés et les concepts inhérents à la mesure et à la géométrie et de les approfondir. L’enseignement des mathématiques, pendant ces années d’études, doit favoriser la création de liens étroits entre les apprentissages essentiels liés à la mesure ainsi qu’à la géométrie (par exemple, déterminer les attributs mesurables de quadrilatères ou de prismes).
« La géométrie nous aide à représenter et à décrire, de façon ordonnée, les objets qui nous entourent et leurs relations spatiales. En outre, l’acquisition d’un sens approfondi des relations spatiales et une maîtrise des concepts et du langage de la géométrie permettent aux élèves d’améliorer leur compréhension des concepts liés à la mesure et à la numération. »
(Ministère de l’Éducation de l’Ontario, 2005a, p. 9).
« Le mot géométrie signifie « mesure de la Terre » et concerne directement la mesure et le déplacement d’objets dans l’espace. La géométrie est le fondement des mathématiques telles que nous les connaissons aujourd’hui; elle a été développée pour expliquer des phénomènes et résoudre des problèmes directement liés à la vie de tous les jours, par exemple, la mesure du temps et la navigation en mer. La pensée spatiale a donné naissance aux plus anciennes formes de pensée mathématique sophistiquée. »
(Ministère de l’Éducation de l’Ontario, 2014, p. 3).
« L’étude des concepts et des habiletés liés à la mesure présente des applications directes au monde dans lequel les élèves évoluent. […] Au fur et à mesure que les élèves renforcent leurs habiletés en numération, elles et ils devraient pouvoir résoudre des problèmes de mesure de plus en plus complexes, ce qui renforce leurs connaissances en algèbre comme en géométrie. »
(Ministère de l’Éducation de l’Ontario, 2005a, p. 9).
Source : Guide d'enseignement efficace des mathématiques de la 7e à la 10e année, p. 6-7.
Niveaux de pensée en géométrie
« Même si les élèves doivent apprendre le vocabulaire propre à la géométrie, l’apprentissage de cette terminologie ne devrait pas constituer l’aspect principal du programme. L’accent devrait plutôt être mis sur l’exploration et la compréhension des rapports entre les formes et sur le développement de la pensée géométrique. »
(Ministère de l’Éducation de l’Ontario, 2005, p. 9).
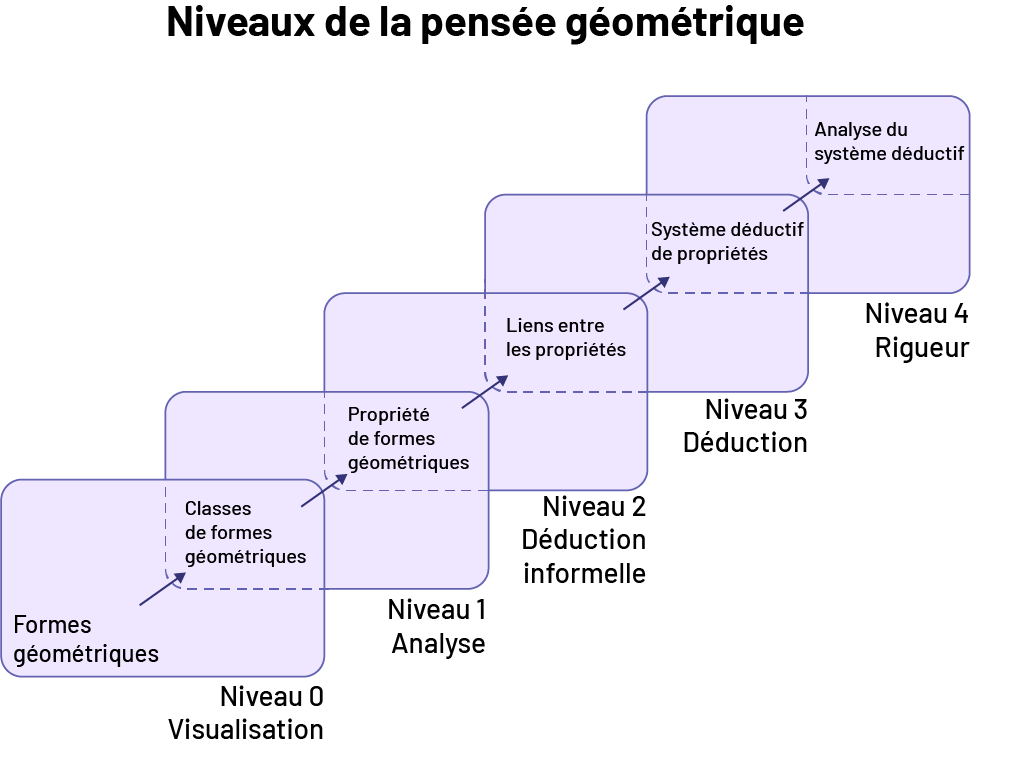
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 12.
Selon Braconne-Michoux (2014), les chercheurs Dina Van Hiele-Geldof et Pierre Van Hiele sont les premiers à avoir conçu un modèle pour décrire les niveaux de pensée en géométrie. Il s’agit d’un modèle à cinq niveaux qui a été adapté au cours des dernières décennies et qui est encore reconnu aujourd’hui. Les élèves peuvent progresser d’un niveau de pensée à un autre dans la mesure où elles et ils font des activités visant la comparaison et la classification de formes géométriques, ainsi que l’analyse des propriétés de ces formes. Le personnel enseignant qui reconnaît les niveaux de pensée des élèves, en se fiant à certains comportements observables, est davantage en mesure de les aider à réaliser des analyses géométriques et à développer progressivement leur capacité à raisonner.
DESCRIPTION | COMPORTEMENTS OBSERVABLES | EXEMPLES |
Niveau 0 – Identification/visualisation Perception et classement des formes géométriques selon leur aspect global sans établir de liens entre les formes géométriques et leurs propriétés. | L’élève :
| L’élève :
|
Niveau 1 – Analyse Analyse des formes géométriques pour en découvrir les propriétés. | L’élève :
| L’élève :
|
Niveau 2 – Déduction informelle Établissement de liens entre les formes géométriques et entre les propriétés d’une forme géométrique donnée. | L’élève :
| L’élève :
|
Niveau 3 – Déduction Étude des définitions, des preuves des théorèmes, des axiomes et des postulats. | L’élève :
| L’élève :
|
Niveau 4 – Rigueur Préoccupation au sujet de la nature même du système axiomatique. Note : Cette préoccupation dépasse largement les objectifs d’enseignement de la géométrie au secondaire. |
L’amélioration de la capacité des élèves à argumenter vient de l’expérience qu’elles et ils acquièrent en découvrant et en explorant les propriétés géométriques de figures, en organisant les figures, en les comparant avec d’autres et en les associant à un vocabulaire précis. Par conséquent, une ou un élève pourrait atteindre des niveaux de pensée différents selon l’apprentissage effectué pour un objet en particulier. Le personnel enseignant ne devrait donc pas déterminer un niveau de pensée en géométrie correspondant à l’ensemble des connaissances de l’élève, mais plutôt à des apprentissages plus précis.
Chaque niveau de pensée en géométrie est associé à un langage précis. Un même mot peut évoquer des idées particulières chez des élèves d’années d’études différentes. Le mot carré, par exemple, véhicule certaines informations pour l’élève du primaire qui s’engage dans une activité lui demandant de classer des formes géométriques de même famille. Toutefois, l’élève du cycle intermédiaire peut reconnaître que, dans un carré, les diagonales sont de mêmes longueurs et se coupent en leur milieu, ce qui lui permet de résoudre un problème en partant de ces caractéristiques. (Inspiré de Braconne-Michoux, 2014, p. 26)
Au cycle intermédiaire, l’objectif est de faire progresser les élèves. Néanmoins, l’atteinte du niveau 2 est souhaitable pour chacune des années d’études. Cet objectif est le même que celui du développement du processus de raisonnement, selon lequel l’élève peut déduire, justifier et conclure.
Source : Guide d'enseignement efficace des mathématiques de la 7e à la 10e année, p. 20-23.
Le sens de la mesure
En mesure, acquérir le sens de la mesure est l’objectif à atteindre, tout comme développer le sens du nombre est le but en numération. Le sens de la mesure comprend les trois composantes suivantes : la compréhension des concepts, la compréhension des relations et la compréhension des procédures. Il existe un lien étroit entre ces trois éléments.
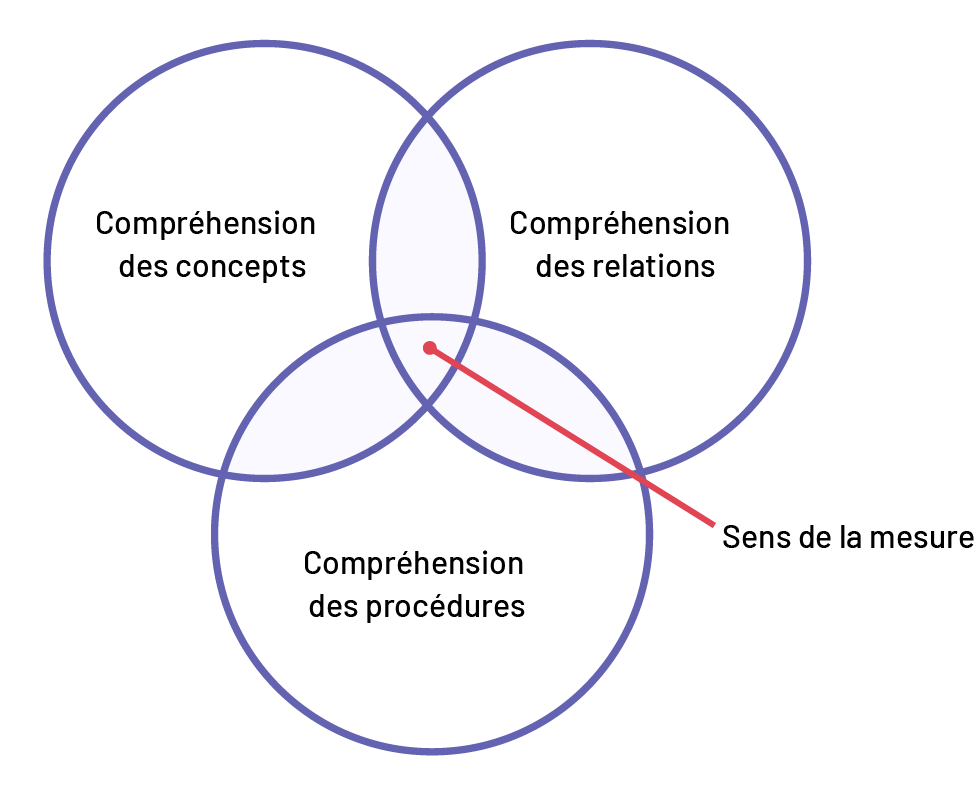
- Les élèves doivent avoir une compréhension conceptuelle des attributs mesurables d’un objet ainsi que des concepts fondamentaux qui donnent un sens aux unités de mesure et à l’acte de mesurer. À l’intermédiaire (7e et 8e année), les attributs mesurables étudiés sont la longueur, l’aire, le volume et les angles de figures planes et de solides. Les concepts fondamentaux liés à ces attributs sont l’itération, la structure associée aux unités de mesure, la transitivité, la conservation et l’additivité.
- Les élèves doivent pouvoir établir diverses relations entre des unités de mesure conventionnelles ainsi qu’entre des attributs. Elles et ils seront donc capables de déterminer et de comparer les mesures de figures et de solides. L’établissement de ces relations facilitera la formulation de conjectures et de généralisations.
- Les élèves doivent développer une aisance à se servir de diverses procédures liées à l’acte de mesurer qui comprend plusieurs étapes. L’acte de mesurer constitue un ensemble de réflexions, de décisions et d’actions permettant d’obtenir une mesure exacte.
Les apprenantes et les apprenants qui commencent au cycle intermédiaire ont déjà acquis un certain bagage en mesure. Elles et ils ont exploré différents attributs mesurables d’objets ainsi que les concepts fondamentaux qui les sous-tendent. Elles et ils ont aussi établi certaines relations entre des mesures conventionnelles et ont développé diverses habiletés à mesurer avec exactitude.
Pour que les élèves approfondissent le sens de la mesure, les activités de résolution de problèmes doivent exiger d’elles et d’eux d’aller au-delà de l’application de procédures et de l’emploi d’instruments de mesure. Selon le document Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Mesure (Ministère de l’Éducation de l’Ontario, 2010) :
« […] les élèves doivent aussi apprendre à reconnaître et à comprendre le sens des attributs mesurables d’un objet, à estimer leur grandeur et à les mesurer dans divers contextes afin que le vrai sens de la mesure puisse s’ancrer dans leurs expériences d’apprentissage, et qu’il les aide à résoudre divers problèmes de la vie et à prendre des décisions éclairées. »
(p. 6)
Source : Guide d'enseignement efficace des mathématiques de la 7e à la 10e année, p. 39-40.
La mesure et la géométrie
« Pour assurer un apprentissage en mesure, il est primordial d’établir des liens avec les concepts géométriques. La géométrie décrit des formes à deux et à trois dimensions, des êtres vivants et des objets inanimés que l’on peut mesurer. Puisqu’il existe de nombreuses relations entre le domaine de la géométrie et celui de la mesure, une bonne compréhension en géométrie influence la compréhension en mesure, et vice-versa. »
(Florida Department of Education, 2011, traduction libre. © Florida Department of Education, 2019. Relating Geometry to Measurement – Tous droits réservés.).
La mesure et la géométrie sont au cœur de nos activités journalières et, par le fait même, elles nous aident à comprendre le monde qui nous entoure. L’observation et la description d’un objet nécessitent de maîtriser des concepts liés à ces deux domaines. Les applications de la mesure en géométrie sont nombreuses et variées, que ce soit pour expliquer la forme d’une bulle de savon, déterminer la popularité d’une page Web ou estimer la population dans certaines circonscriptions. Mesurer implique de rendre explicites les conjectures formulées au moment de la résolution de problèmes. Par exemple, pour déterminer l’importance d’une page Web, il suffit de se fier au nombre de liens associés à d’autres pages Web.
L’utilisation de mesures en géométrie aide à déterminer une longueur, une aire ou un volume inconnu en se servant de mesures connues de représentations de figures à deux et à trois dimensions. Les mesures peuvent être calculées à partir d’attributs tels que la longueur des côtés, l’aire des faces ou les coordonnées d’une figure dans un plan cartésien.
- Pour construire et mesurer le périmètre ou l’aire de figures planes complexes (composées), les élèves doivent avoir l’occasion de décomposer des figures ou de réorganiser les parties de figures en d’autres figures simples telles que des cercles, des polygones ou d’autres figures.
- Pour calculer le périmètre, l’aire ou le volume de solides, les élèves doivent réaliser des activités leur permettant de décomposer des solides et de les réorganiser en construisant des sphères, des cônes, des pyramides ou des prismes et même en assemblant autrement des parties de solides. Des activités d’estimation de mesures de solides fournissent aux élèves une stratégie utile pour calculer les dimensions de solides irréguliers.
Exemple
« Le volume du prisme A est le même que celui du prisme B, car si on décompose le prisme A en deux prismes identiques et qu’on les superpose, on obtient le prisme B »
(Ministère de l’Éducation de l’Ontario, 2010c. p. 136).

En somme, certains concepts essentiels appuient l’apprentissage de la mesure intégrée à la géométrie.
- Calculer l’aire et le volume d’une forme géométrique en la décomposant en formes géométriques plus simples ou en réorganisant ses parties.
- Estimer des mesures à l’aide de différents outils, y compris la technologie, appuie le développement du sens de la mesure.
- Calculer le périmètre, l’aire ou le volume de l’image d’une figure connue à la suite d’une transformation, en utilisant des rapports et des proportions.
Source : Guide d'enseignement efficace des mathématiques de la 7e à la 10e année, p. 54-55.
Habileté à visualiser
« L’habileté à visualiser est un processus qui permet à l’élève de se représenter des concepts abstraits sous forme d’images mentales. Ces images lui permettent de manipuler les concepts, de les rendre signifiants et de se les approprier. »
(Small, 2006, p. 132, traduction libre).
L’habileté à visualiser correspond à la capacité de se faire une image mentale d’une situation ou d’un concept abstrait. En mesure, cette habileté est liée principalement à la capacité de se faire une image mentale :
- de certains attributs mesurables;
- de repères associés aux divers attributs.
Visualiser certains attributs mesurables : La capacité de se faire une image mentale de certains attributs mesurables aide les élèves à mieux en comprendre le sens. Au cycle intermédiaire, les élèves doivent développer l’habileté à visualiser les attributs volume, longueur, aire et angles.
Visualiser des repères : La capacité de se faire une image mentale de certains repères associés aux attributs mesurables aide les élèves à estimer la grandeur d’un attribut ou à vérifier la vraisemblance d’un résultat obtenu à la suite de l’utilisation d’un instrument de mesure ou de l’application d’une formule.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 20-22.
Au cycle intermédiaire, les élèves poursuivent l’étude des propriétés des figures planes et des solides au moyen de représentation sur papier (par exemple, représentation sur du papier quadrillé, du papier à points).
Ces activités aident les élèves à se construire une représentation mentale des figures planes et des solides fondée sur des propriétés précises et favorisent le développement d’habiletés liées à la visualisation.
Afin de se construire une bonne représentation mentale des solides, les élèves doivent être en mesure de les visualiser aussi bien dans l’espace bidimensionnel des figures planes que dans l’espace tridimensionnel des solides.
Pour les aider à développer l’habileté à passer d’un espace à l’autre et à consolider leurs connaissances des propriétés des solides, le personnel enseignant peut avoir recours à diverses activités de construction et à diverses activités de représentation (par exemple, tracer le développement d’un solide, associer un solide à son développement ou à ses vues de face, de côté et de dessus).
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 28-30.
La visualisation spatiale est un type particulier de pensée spatiale qui implique l’utilisation de notre imagination pour « générer, mémoriser, extraire et transformer des images visuelles bien structurées » (Lohman, 1996, traduction libre, p. 98); elle est parfois considérée comme étant la capacité à penser avec l’« intelligence de l’œil ».
(Ministère de l’Éducation de l’Ontario, 2014, p. 10).
La visualisation spatiale se développe en mobilisant certaines habiletés spatiales qu’a énumérées John Del Grande (1990), y compris la rotation mentale.
| HABILETÉS SPATIALES RELATIVES À LA VISUALISATION SPATIALE | DESCRIPTION |
| 1. Coordination oculomotrice | Habileté à coordonner la vue et les mouvements du corps. |
| 2. Perception de plans (forme et fond) | Habileté à percevoir un élément précis figurant sur une toile de fond complexe (intersections, superpositions). |
| 3. Constance des formes | Habileté à reconnaître des figures géométriques indépendamment de leur taille, de leur couleur et de leur orientation dans l’espace. |
| 4. Perception des positions | Habileté à percevoir la position d’un objet par rapport à soi. Habileté à discriminer des objets identiques, peu importe leur orientation. |
| 5. Perception des relations spatiales | Habileté à percevoir la position d’au moins deux objets par rapport à soi ou d’un objet par rapport à l’autre. |
| 6. Discrimination visuelle | Habileté à remarquer les ressemblances et les différences entre deux ou plusieurs objets. |
| 7. Rotation mentale | Habileté à « […] faire tourner mentalement des objets bidimensionnels ou tridimensionnels » (Ministère de l’Éducation de l’Ontario, 2014, p. 13). |
(John Del Grande, 1990. © 2019, National Council of Teachers of Mathematics. The Arithmetic Teacher, vol. 37, no 6.)
Source : Guide d'enseignement efficace des mathématiques de la 7e à la 10e année, p. 12-13.
Habileté à résoudre une situation-problème
L’habileté à résoudre des problèmes est un processus essentiel dans l’apprentissage de la mesure. Afin d’aider les élèves à développer cette habileté, le personnel enseignant doit leur présenter divers types de situations-problèmes dont le contexte est signifiant. Il doit les inciter à faire appel à leurs connaissances antérieures ainsi qu’à leurs stratégies en littératie et en résolution de problèmes, à communiquer clairement leurs résultats et à discuter des idées de leurs pairs lors d’échanges mathématiques. En étant ainsi engagées et engagés de manière optimale dans une réflexion portant sur les concepts visés, les élèves en clarifient le sens.
Les situations-problèmes en mesure doivent contribuer à améliorer la compréhension des élèves en ce qui a trait aux attributs et aux concepts fondamentaux et aux relations. Il est essentiel que les élèves participent activement à la résolution des problèmes et aux discussions qui s’ensuivent. Ces expériences variées leur permettent de développer leur sens de la mesure.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 23.
Habileté à raisonner
« Le raisonnement spatial ou l’intelligence spatiale est la capacité d’imaginer, [de] visualiser et [de] différencier des objets en deux ou [en] trois dimensions. Elle contribue au potentiel à comprendre, [à] manipuler et [à] modifier des données complexes et [à] traduire des concepts en idées concrètes. »
(MyRHline, 2017).
Selon le ministère de l’Éducation de l’Ontario (2014), dans le document Mettre l’accent sur le raisonnement spatial M-12 :
« [i]l est crucial que l’intervention en mathématiques soit précoce […]. » (Sinclair et Bruce, 2014)
Mais nous savons aussi que l’importance de la pensée spatiale augmente pendant l’adolescence, à mesure que les élèves étudient un curriculum de plus en plus abstrait les conduisant à des mathématiques de haut niveau, car « l’espace est plus étroitement associé aux mathématiques au cours des études supérieures. » (Mix et Cheng, 2012, traduction libre, p. 219).
(Ministère de l’Éducation de l’Ontario, 2014, p. 15).
Source : Guide d'enseignement efficace des mathématiques de la 7e à la 10e année, p. 8.
Voici un exemple de contenu d’un domaine d’études favorisant le développement du raisonnement spatial, tiré des programmes-cadres de mathématiques de l’Ontario, Sens de l’espace, 7e année :
– utiliser les relations entre le rayon, le diamètre et la circonférence d’un cercle pour expliquer la formule de calcul de la circonférence d’un cercle et pour résoudre des problèmes connexes.
Dans une classe de mathématiques axée sur le développement du raisonnement, le personnel enseignant privilégiera aussi le raisonnement géométrique. Cette attente vise, en particulier, le développement des habiletés liées à la déduction et à la présentation d’arguments mathématiques cohérents. Le personnel enseignant, qui demande aux élèves les raisons pour lesquelles leur affirmation est vraie, doit observer la manière dont elles et ils abordent la question pour les aider à progresser dans l’acquisition d’habiletés en géométrie. Selon les recherches portant sur la pensée géométrique (Van Hiele, Uziskin, Burger et Shaughnessy, et Braconne-Michoux), la façon dont les élèves justifient leur raisonnement géométrique montre leur niveau de pensée en géométrie. L’élève qui, par exemple, justifie qu’un triangle est isocèle, car il ressemble à un chapeau pointu, devra éventuellement réussir à verbaliser cette caractéristique en disant qu’au moins deux des côtés du triangle ou deux de ses angles sont congrus.
Source : Guide d'enseignement efficace des mathématiques de la 7e à la 10e année, p. 20.
Habileté à communiquer
La communication orale ou écrite demeure un élément clé pour assurer chez les élèves une compréhension en profondeur des concepts. Le rôle du personnel enseignant est de faciliter la communication mathématique au moment de l’exploration et pendant les échanges mathématiques en petits groupes ou en groupe-classe. Le personnel enseignant encourage les élèves à faire part aux autres de leurs hypothèses et à les justifier à l’aide d’arguments convaincants et d’un vocabulaire approprié. De plus, il doit susciter la réflexion des élèves en les encourageant à expliquer leur raisonnement pendant les échanges et les moments de consolidation. Les discussions doivent être orientées de façon à leur permettre d’établir des liens entre les différentes représentations et les concepts mathématiques.
Source : Guide d'enseignement efficace des mathématiques de la 7e à la 10e année, p. 36.
Habileté à abstraire
Au cycle primaire, la pensée géométrique des élèves se situe généralement aux niveaux 0 et 1. Au début, les élèves apprennent à reconnaître les formes géométriques, à les nommer et à énumérer certains de leurs attributs physiques (par exemple, la sphère est ronde et elle roule). Plusieurs se construisent alors une représentation mentale des formes géométriques en les associant à des objets connus (par exemple, un rectangle ressemble à une porte, une sphère ressemble à un ballon). Dans certains cas, cette représentation est tellement ancrée qu’elle les empêche de concevoir une orientation de la forme autre que celle qui correspond à la représentation qu’elles et ils en ont. Voir les figures ci-dessous.

Par la suite, les élèves délaissent progressivement les références aux attributs physiques et aux objets connus au fur et à mesure qu’elles et ils apprennent à décrire les formes géométriques en fonction d’une liste de propriétés nécessaires (par exemple, un rectangle est une figure plane qui a quatre côtés, quatre angles droits et des côtés opposés qui sont congrus et parallèles).

Aux cycles moyen et intermédiaire, la pensée géométrique des élèves progresse vers le niveau 2 au fur et à mesure que leur capacité d’abstraction se développe. Cette capacité est liée à la faculté de concentrer son attention sur certaines propriétés de façon isolée. Elle leur permet, entre autres, de choisir parmi la liste de propriétés nécessaires d’une forme géométrique, celles qui suffisent à la définir (propriétés suffisantes).
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 32-33.
Il importe que le personnel enseignant soit conscient que, pour développer les habiletés et les concepts relatifs à la mesure et à la géométrie, les élèves doivent acquérir certaines habiletés spatiales. Cependant, selon le document Mettre l’accent sur le raisonnement spatial M-12 (Ministère de l’Éducation de l’Ontario, 2014), « [t]ous les types d’habiletés inhérentes à la pensée spatiale ne sont pas liés aux résultats en mathématiques dans la même mesure. L’apprentissage des mathématiques dépend plus de certaines habiletés de pensée spatiale que d’autres. » Le personnel enseignant doit donc aider les élèves à développer particulièrement leur visualisation spatiale et leur mémoire visuo-spatiale.
Il est évident que la construction ou la description de formes géométriques exige un raisonnement spatial. Cependant, le personnel enseignant doit aussi se rendre compte que, pour estimer, les élèves utilisent des stratégies qui exigent une pensée spatiale et, en particulier, la visualisation spatiale.
Tout en tenant compte des éléments propres au développement du raisonnement spatial, le personnel enseignant doit intégrer les éléments essentiels d’un enseignement efficace des mathématiques, notamment les compétences liées à la communication et à la résolution de problèmes.
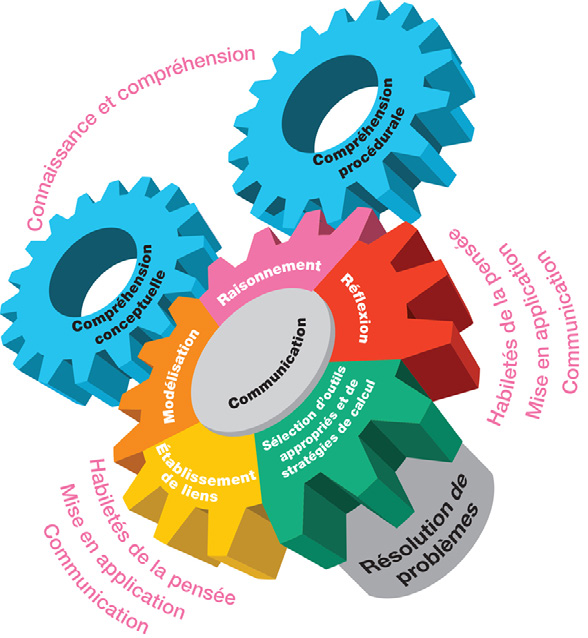 image Infographie.Un engrenage est placé sur un axe nommé « résolution de problèmes ». La roue d’engrenage, qui est sur cet axe, est divisée en 5 parties : la réflexion ; sélection d’outils appropriés et de stratégies de calcul ; établissement de liens ; modélisation ; et raisonnement. Le tout atournant autour de la communication.Ces cinq éléments permettent : les habiletés de la pensée, la mis en application et la communication. Sur les engrenages, modélisation et raisonnement, on retrouve une autre roue de compréhension conceptuelle, et une roue de compréhension procédure. Ce qui apportera la connaissance et compréhension.
image Infographie.Un engrenage est placé sur un axe nommé « résolution de problèmes ». La roue d’engrenage, qui est sur cet axe, est divisée en 5 parties : la réflexion ; sélection d’outils appropriés et de stratégies de calcul ; établissement de liens ; modélisation ; et raisonnement. Le tout atournant autour de la communication.Ces cinq éléments permettent : les habiletés de la pensée, la mis en application et la communication. Sur les engrenages, modélisation et raisonnement, on retrouve une autre roue de compréhension conceptuelle, et une roue de compréhension procédure. Ce qui apportera la connaissance et compréhension.L’enseignement selon les niveaux de pensée en géométrie
Selon Van de Walle et Lovin (2008), les explorations en géométrie que propose aux élèves le personnel enseignant sont les principaux facteurs qui déterminent la progression des apprenantes et des apprenants sur l’échelle du développement de la pensée géométrique. Les élèves progressent dans les divers niveaux de pensée en géométrie dans la mesure où elles et ils font des activités d’exploration, de manipulation, de construction, de visualisation, de comparaison et de transformation. Les activités d’exploration doivent leur permettre d’établir des relations entre les concepts géométriques afin de construire des idées signifiantes. De plus, la façon d’interagir avec elles et eux peut les inciter à passer à un niveau supérieur ou, tout au moins, à les mettre au défi de le faire.
Les niveaux de pensée en géométrie décrivent les idées des élèves relatives à la géométrie et la façon dont elles et ils perçoivent les formes. Chaque niveau est défini comme une suite de comportements logiques. L’élève qui progresse d’un niveau à un autre modifie sa pensée lorsqu’elle ou il décrit, perçoit ou compare les formes géométriques.
D’autres éléments entrent en jeu dans le développement des niveaux de pensée en géométrie.
- Les niveaux sont séquentiels. Pour passer à un niveau plus élevé, les élèves doivent développer les idées et la compréhension relatives à un concept géométrique du niveau précédent.
- Les niveaux de pensée en géométrie ne dépendent pas de l’âge des élèves ni de l’année d’études. Certains adultes se situent au niveau 0. Les élèves peuvent se situer au niveau 1 (analyse) concernant la compréhension d’un concept et au niveau 0 (visualisation) en ce qui a trait à la maîtrise d’un autre concept. Par exemple, elles et ils décrivent certaines propriétés du carré (niveau 1 : analyse), mais ne reconnaissent le parallélogramme qu’à cause de son apparence (niveau 0 : identification-visualisation).
- Les élèves passent d’un niveau à un autre selon leur compréhension des différents concepts.
- Les élèves qui se situent au niveau 2 ont acquis les niveaux 0 et 1.
- Les facteurs qui influencent le plus le développement de la pensée géométrique sont les activités adaptées au niveau de pensée en géométrie des élèves. Le niveau de pensée en géométrie des apprenantes et des apprenants dépend des concepts enseignés et des stratégies utilisées.
Note : Les cinq niveaux du développement de la pensée géométrique qu’ont décrits Van Hiele et Van Hiele-Geldof ne sont aucunement liés aux quatre niveaux de rendement de la grille d’évaluation du rendement du programme-cadre de mathématiques.
L’enseignement au niveau 0 (identification-visualisation)
Au niveau 0, le personnel enseignant doit fournir aux élèves de nombreuses occasions de classer des objets géométriques. Il convient de mettre l’accent sur les similitudes et les différences entre les formes géométriques.
Une idée clé en géométrie est celle de l’invariabilité. Une part importante du temps consacré à l’étude de la géométrie devrait être employée à déterminer les changements possibles pour qu’une propriété reste vraie. Par exemple, la somme des mesures des angles intérieurs d’un triangle ne varie pas, quels que soient les changements que peut subir un triangle. Ironiquement, plus le personnel enseignant impose des contraintes sur ce qui peut être changé, plus elle ou il aide les élèves à relever des propriétés intéressantes. Par exemple, au moment de l’exploration de la mesure des angles intérieurs et extérieurs de polygones, la contrainte de limiter l’exploration aux quadrilatères permettrait de vérifier si certaines propriétés relevées s’appliquent aux quadrilatères convexes ou concaves.
Une contrainte supplémentaire qui consisterait à limiter l’exploration à des cas particuliers de quadrilatères tels que les parallélogrammes, les cerfs-volants et les losanges, aiderait les élèves à déterminer ce qui est invariable.
L’enseignement au niveau 1 (analyse)
Au niveau 1, le personnel enseignant propose aux élèves des activités de construction de formes géométriques pour leur donner l’occasion d’analyser divers cas. Les activités de construction dynamique aident les élèves de ce niveau à progresser. Elles et ils peuvent explorer la construction de formes géométriques et, par la suite, grouper les formes en différentes classes en fonction de leurs caractéristiques.
L’enseignement au niveau 2 (déduction informelle)
Au niveau 2, le personnel enseignant aide les élèves à développer des habiletés liées à la déduction informelle en utilisant un vocabulaire approprié. Les élèves développent ces habiletés en acquérant de l’expérience afin de comprendre des énoncés relatifs à la déduction informelle; par exemple : « Si c’est ______, alors c’est aussi ___. »; « Tous les ____ sont des ____. » Des énoncés, comme ceux présentés ci-dessous, aident les apprenantes et les apprenants à raisonner et à acquérir le vocabulaire propre à la déduction informelle.
- Si c’est un rectangle, alors c’est aussi un parallélogramme.
- Tous les carrés sont des rectangles.
- Certains parallélogrammes sont des losanges.
Il importe d’inciter les élèves à examiner les propriétés d’une classe de figures afin de déterminer les propriétés nécessaires et les propriétés suffisantes pour décrire une forme géométrique. Une propriété nécessaire, si elle était retirée d’une description, ne définirait plus uniquement la figure en question. Par exemple, en enlevant la propriété qu’un carré a au moins un angle droit, pour garder la propriété qu’un carré a quatre côtés congrus, on décrit le carré, mais aussi le losange. Pour décrire le carré, il est donc nécessaire d’avoir deux propriétés, soit celle concernant la longueur de ses côtés et celle liée aux angles droits. C’est à partir de la 6e année que les élèves commencent à explorer les diagonales des quadrilatères. Elles et ils constatent alors qu’il est suffisant de ne décrire que les diagonales pour classer des quadrilatères. Par exemple, les élèves n’ont qu’à dire que les diagonales de la figure ont la même longueur et se croisent en leur milieu à un angle droit pour décrire le carré. Les autres propriétés ne sont plus nécessaires.
Propriétés nécessaires Les propriétés nécessaires d’une forme géométrique constituent l’ensemble des propriétés que possède cette forme. | Propriétés suffisantes Les propriétés suffisantes d’une forme géométrique constituent une liste minimale de propriétés qui suffisent à définir la forme. Cette liste forme donc un sous-ensemble de l’ensemble des propriétés nécessaires. |
Il faut encourager les élèves à énoncer des hypothèses et à les vérifier. Ainsi, à l’aide de questions du type « Pourquoi…? », elles et ils peuvent tenter de déterminer les raisons pour lesquelles il y a des relations particulières entre certains éléments d’une forme géométrique.
Source : Guide d'enseignement efficace des mathématiques de la 7e à la 10e année, p. 24-27.
