Fondements généraux du domaine Sens de l'espace
Cycle moyen
Dans le programme-cadre de mathématiques 2020, le domaine Sens de l’espace intègre les deux domaines déjà connus comme Mesure et Géométrie et sens de l’espace à cause des liens indissociables entre eux. Dans les prochaines sections, vous trouverez les fondements des deux domaines (Mesure et Géométrie et sens de l’espace) des guides d’enseignement efficace des mathématiques.
Sens de l’espace
« Le sens de l’espace est la conscience intuitive que l’on a de son environnement et des objets qui s’y trouvent. »
(Ministère de l’Éducation de l’Ontario, 2005, p. 9).
Bien que le sens de l’espace sous-tende l’apprentissage de concepts géométriques, il joue aussi un rôle déterminant dans le développement du sens de la mesure. Selon Piaget (cité dans Lehrer, 2003, p. 180), la compréhension de la mesure entraîne une restructuration mentale de l’espace et englobe ainsi de plus en plus de subdivisions de l’espace. Ces subdivisions se traduisent par une quantité, une mesure.
Selon Clements (1999, p. 73), le sens de l’espace des enfants comme celui des adultes dépend de cartes mentales qui ne ressemblent en rien à la photo d’une carte papier ou électronique. Elles sont formées de connaissances ou de caractéristiques personnelles et comportent différentes idées ainsi que divers processus qui peuvent s’organiser selon des schèmes de référence variés. Plus l’enfant est jeune, plus les liens entre les représentations sont vagues. Ces représentations relèvent davantage de l’ordre spatial que visuel. Afin de faire preuve d’un sens de l’espace, les élèves doivent posséder des habiletés spatiales, notamment l’orientation spatiale et la visualisation. Grâce à l’orientation spatiale, elles et ils peuvent situer leur position par rapport à des objets ou à des points dans l’espace et peuvent se déplacer dans leur milieu. Les élèves comprennent et établissent des liens entre leurs différentes positions dans l’espace. Quant à la visualisation, elle leur permet de créer des images mentales, de les manipuler et de s’en servir pour faciliter la résolution de problèmes.
Le tableau ci-dessous résume la façon dont sont définies ces deux habiletés spatiales dans le contexte de mesure et de la géométrie.
Habileté | Exemples |
Orientation spatiale Habileté à se situer ou à situer des objets dans son espace physique immédiat, et à effectuer ou à décrire des déplacements dans cet espace. |

|
Visualisation Habileté à se former et à décrire une représentation mentale de lieux, d’objets et de déplacements dans un espace bidimensionnel ou tridimensionnel. |
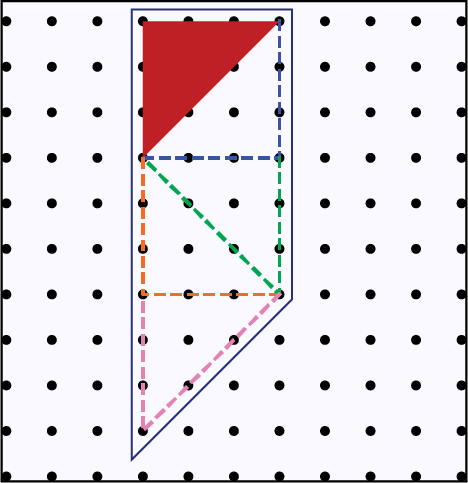
|
Source : Guide d'enseignement efficace des mathématiques de la maternelle à la 3e année, p. 9-11.
Fondements en géométrie (E1)
La géométrie et le sens de l’espace au cycle moyen, c’est le développement :
- d’une compréhension des formes géométriques, de leurs propriétés et des interrelations entre elles;
- d’une conscience intuitive de la position et du déplacement d’objets dans l’espace;
- d’un raisonnement déductif informel et d’un raisonnement spatial complexe qui permettent aux élèves de résoudre des problèmes dans tous les domaines des mathématiques et dans diverses situations de la vie courante à l’école, à la maison ou au jeu.
La géométrie et le sens de l’espace au cycle moyen, ce n’est pas :
- un savoir inné reçu à la naissance par quelques rares individus;
- un enseignement ou un apprentissage centré uniquement sur les règles, les procédures, le raisonnement analytique et les démonstrations;
- une mémorisation de définitions et de propriétés;
- uniquement la classification des figures planes et des solides.
La géométrie et le sens de l’espace sont indissociables puisque la géométrie nous aide à décrire, à représenter et à mathématiser la réalité spatiale et que le sens de l’espace nous permet de visualiser, de reconnaître ou d’apprécier cette réalité.
Niveaux de pensée en géométrie
« Même si les élèves doivent apprendre le vocabulaire propre à la géométrie, l’apprentissage de cette terminologie ne devrait pas constituer l’aspect principal du programme. L’accent devrait plutôt être mis sur l’exploration et la compréhension des rapports entre les formes et sur le développement de la pensée géométrique. »
(Ministère de l’Éducation de l’Ontario, 2005, p. 9).
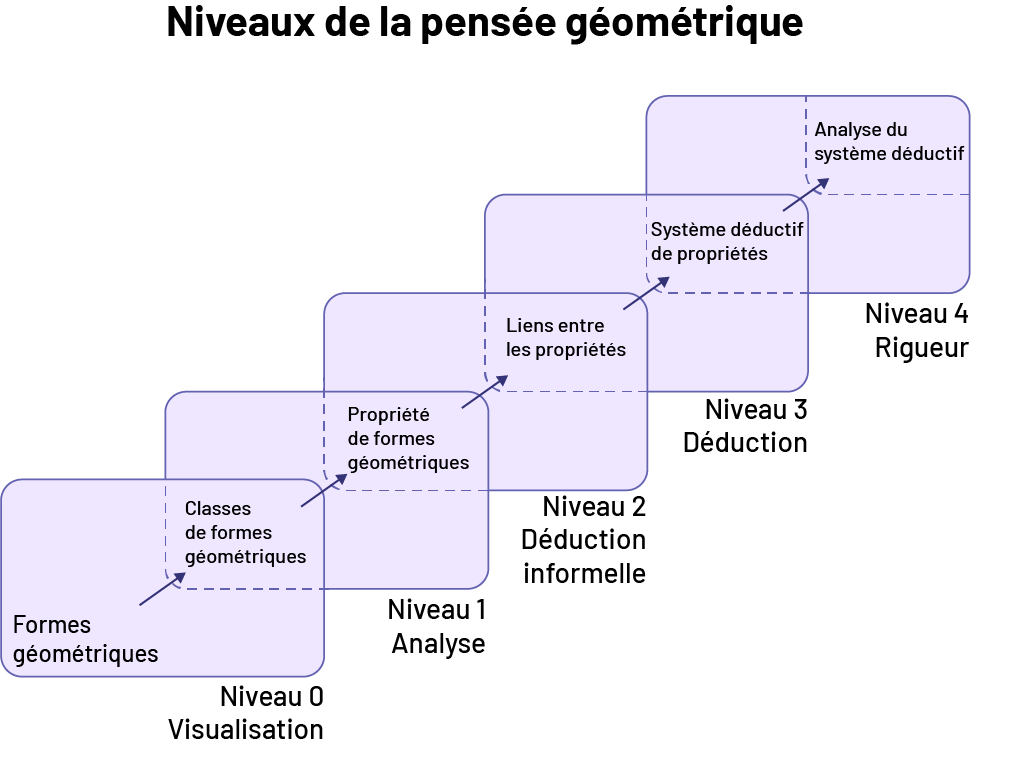 image Niveaux de la pensée géométrique. Niveau zéro : visualisation. Niveau un : analyse. Niveau 2 : déduction informelle. Niveau 3 déduction.Niveau 4 : Rigueur. Chaque niveau est accompagné d’une carte avec une note. En partant du niveau zéro, formes géométriques, classes de formes géométriques, un, propriété de formes géométriques, 2, liens entre les propriétés, 3, système déductif de propriétés, 4, analyse du système déductif.
image Niveaux de la pensée géométrique. Niveau zéro : visualisation. Niveau un : analyse. Niveau 2 : déduction informelle. Niveau 3 déduction.Niveau 4 : Rigueur. Chaque niveau est accompagné d’une carte avec une note. En partant du niveau zéro, formes géométriques, classes de formes géométriques, un, propriété de formes géométriques, 2, liens entre les propriétés, 3, système déductif de propriétés, 4, analyse du système déductif.Deux chercheurs néerlandais, Dina Van Hiele-Geldof et Pierre Van Hiele, ont conçu un modèle à cinq niveaux pour décrire la compréhension des concepts géométriques à différentes étapes du développement de la pensée de l’élève. Une brève description de ces cinq niveaux ainsi que des exemples de comportements observables pour chacun sont présentés dans le tableau suivant.
DESCRIPTION | COMPORTEMENTS OBSERVABLES |
Niveau 0 – Visualisation | Niveau 0 – Visualisation |
Perception des figures géométriques selon leur apparence plutôt que leurs propriétés | L’élève :
Exemple d’énoncé : ✓ C’est un carré parce que ça ressemble à un carré, parce que je le vois, parce que c’est carré. |
Niveau 1 – Analyse | Niveau 1 – Analyse |
Début de l’analyse des formes géométriques pour en découvrir les propriétés | L’élève :
Exemple d’énoncé : ✓ Cette figure est un carré parce qu’elle a quatre sommets. ✓ Cette figure est un carré parce qu’elle a quatre coins droits. ✓ Cette figure est un carré parce qu’elle a quatre côtés égaux. ✓ Cette figure est un carré parce qu’elle a deux paires de côtés parallèles. |
Niveau 2 – Déduction informelle | Niveau 2 – Déduction informelle |
Établissement de liens ou de relations entre les propriétés d’une figure et entre les figures | L’élève :
Exemple d’énoncé : ✓ C’est un carré, mais c’est aussi un trapèze, car la propriété qui décrit le trapèze est qu’au moins deux côtés opposés sont parallèles. Je crois donc que le carré est une sorte de trapèze. ✓ Un carré est un rectangle, un parallélogramme et un quadrilatère parce qu’il possède toutes les propriétés de ces trois polygones. Un cube est aussi un prisme à base carrée ou un prisme à base rectangulaire. |
Niveau 3 – Déduction | Niveau 3 – Déduction |
Étude des définitions, des preuves des théorèmes, des axiomes et des postulats | L’élève :
Exemple d’énoncé : ✓ Un parallélogramme qui a deux côtés adjacents de même longueur doit être un losange. |
Niveau 4 – Rigueur | Niveau 4 – Rigueur |
Étude de la géométrie de façon abstraite Note : Peu de recherches ont été faites sur ce niveau. | L’élève :
|
Selon la théorie, les élèves doivent passer par chacun des niveaux pour chaque nouveau concept. Elles et ils peuvent donc être au niveau 1 (analyse) pour un concept et au niveau 0 (visualisation) pour un autre. À titre d’exemple, une ou un élève peut être capable de décrire certaines propriétés du carré (niveau 1), mais n’être capable de reconnaître le parallélogramme que par son apparence (niveau 0). Les élèves peuvent progresser d’un niveau de pensée à un autre dans la mesure où elles et ils font des activités qui misent sur la comparaison et la classification des formes géométriques, et sur l’analyse de leurs propriétés. Le personnel enseignant qui sait reconnaître le niveau de pensée des élèves par rapport à un concept donné d’après certains comportements observables est davantage en mesure de les aider à comprendre ce concept et à les faire cheminer vers un niveau de pensée plus élevé. De façon générale, la plupart des élèves au cycle primaire se situent principalement aux niveaux de la visualisation et de l’analyse.
Le personnel enseignant au cycle moyen doit les aider à cheminer vers le niveau de la déduction informelle (niveau 2). Ce cheminement se poursuit en 7e et en 8e année, alors que le cheminement vers le niveau de la déduction (niveau 3) se fait habituellement au palier secondaire.
Note : Il est important de retenir que les cinq niveaux de la pensée géométrique ne sont aucunement liés aux quatre niveaux de rendement que l’on trouve dans la grille d’évaluation du rendement du programme-cadre de mathématiques.
Aperçu des grandes idées en géométrie
Les attentes et les contenus d’apprentissage du programme-cadre de mathématiques font appel à un grand nombre de concepts. Les grandes idées aident le personnel enseignant à voir la façon dont ces concepts peuvent être regroupés pour permettre une programmation plus efficace de l’enseignement. En planifiant son enseignement en fonction des grandes idées, ainsi que des concepts et des habiletés qui s’y rattachent, le personnel enseignant est en mesure d’élaborer des situations d’apprentissage cohérentes qui permettent aux élèves :
- d’explorer les concepts en profondeur;
- d’établir des liens entre les différents concepts;
- de reconnaître que les mathématiques forment un tout cohérent et non un éventail de connaissances isolées.
Dans la section qui suit, on trouve les deux grandes idées en géométrie et sens de l’espace, chacune étant appuyée de deux énoncés qui la sous-tendent.
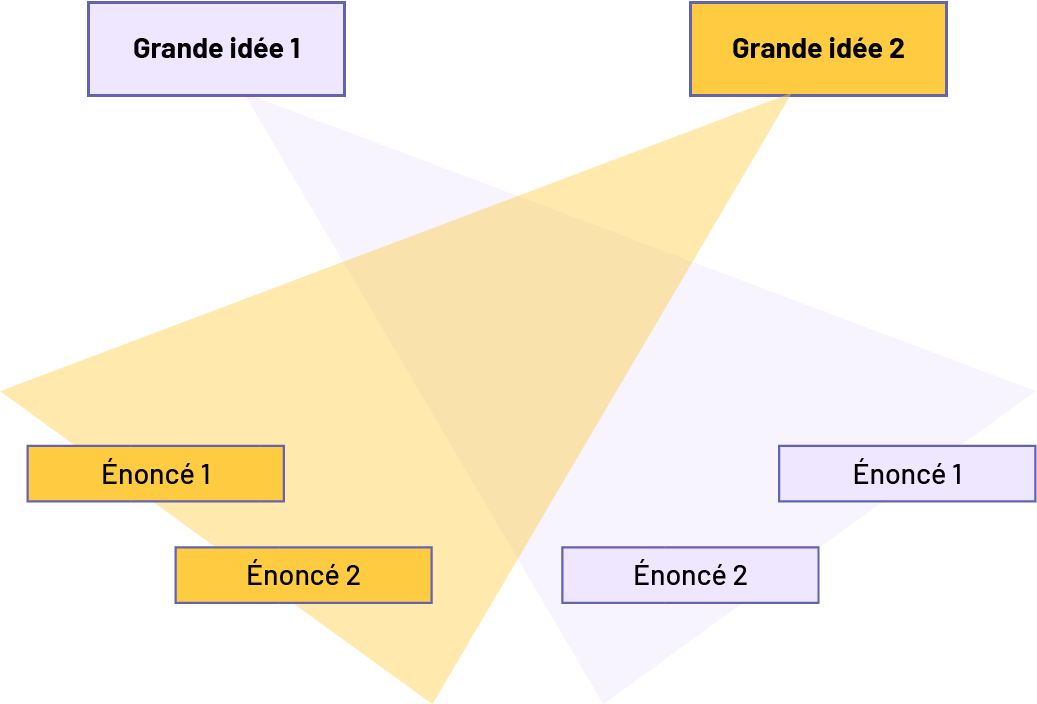
Les deux grandes idées qui constituent la base de l’attente E1 (Raisonnement géométrique) du domaine Sens de l’espace de la 4e à la 6e année sont :
Grande idée 1 : Formes géométriques
La connaissance des formes géométriques et de leurs propriétés permet de mathématiser le monde qui nous entoure.
Énoncé 1 : Propriétés
L’exploration et la construction de diverses représentations d’angles, de figures planes et de solides favorisent le développement de la compréhension de leurs propriétés.
Énoncé 2 : Raisonnement déductif informel
L’analyse des propriétés des figures planes et des solides permet de développer les habiletés de la pensée liées au raisonnement déductif informel.
Grande idée 2 : Position et déplacement
Les concepts de position et de déplacement en géométrie permettent de développer le sens de l’espace bidimensionnel et tridimensionnel.
Énoncé 1 : Systèmes de repérage
Les systèmes de repérage avec coordonnées servent à préciser la position d’un objet dans l’espace.
Énoncé 2 : Transformations
Le déplacement de formes géométriques peut être décrit à l’aide de diverses transformations.
Les deux grandes idées se recoupent et se complètent. Par exemple, le fait de bien comprendre les propriétés des formes géométriques permet de les déplacer et de préciser leur position dans l’espace avec plus de facilité. L’enseignante ou l’enseignant doit aider les élèves à établir des liens entre ces deux grandes idées et entre les concepts qui s’y rattachent, ainsi qu’avec les expériences de la vie quotidienne.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 5-18.
Fondements en mesure (E2)
« Si la mesure s’avère une partie intégrante de nos vies, nous prenons rarement conscience de la variété des mesures auxquelles nous recourons. Au cours d’une journée typique, nous utilisons très peu de mesures précises (par exemple, 350 ml de jus d’orange, 3 g de céréales, 20 l d’essence), mais nous estimons continuellement (par exemple, circuler environ à 50 km/h, faire un trajet d’environ une demi-heure, distribuer environ 25 feuilles). Nous utilisons fréquemment des unités de mesure non conventionnelles telles que trois boîtes de conserve, une pincée de sel, long comme six voitures. Nous recourons à plusieurs mesures comparatives ainsi qu’à des mesures moyennes. »
(Wilson et Rowland, 1993, p. 171, traduction libre).
La mesure jalonne nos activités et oriente, par le fait même, nos réflexions, nos décisions et notre perception du monde. Elle fait partie de nos activités quotidiennes à tel point que l’on en oublie la présence et l’importance. Ainsi, on se pose régulièrement des questions telles que « Cet objet peut-il passer par l’ouverture de la porte? », « Quelle boîte pourrait contenir tous ces objets? », « Laquelle de ces deux destinations est la plus près? », sans nécessairement penser que l’on fait alors appel à une mesure.
Dans toute situation, il est possible de mesurer les différentes caractéristiques d’un objet. Il importe donc de préciser la caractéristique, communément appelée attribut, fait l’objet d’une mesure. Voici quelques exemples d’attributs mesurables que l’on peut quantifier par diverses unités de mesure non conventionnelles et conventionnelles.
acuité visuelle | fréquence | précipitation |
aire | indice de rayons UV | profondeur |
angle | intensité du son | superficie |
capacité | longueur | taille |
circonférence | masse | température |
densité | pente | temps |
distance | périmètre | vitesse |
population | volume | |
facteur de refroidissement |
Attribut : caractère particulier d’un être, d’une chose.
Le sens de la mesure est complexe et fait appel à des compétences qui vont au-delà de l’habileté à mesurer à l’aide d’un instrument de mesure tel qu’une règle, un cylindre gradué, un chronomètre ou un thermomètre. En effet, les élèves doivent aussi apprendre à reconnaître et à comprendre le sens des attributs mesurables d’un objet, à estimer leur grandeur et à les mesurer dans divers contextes afin que le vrai sens de la mesure puisse s’ancrer dans leurs expériences d’apprentissage, et qu’il les aide à résoudre divers problèmes de la vie courante et à prendre des décisions éclairées.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 5-6.
L’enseignement du sens de la mesure au cycle moyen vise à développer la compréhension des élèves en matière de concepts, de relations et de procédures en mesure. Pour atteindre cet objectif, le personnel enseignant doit présenter aux élèves des situations d’apprentissage authentiques qui favorisent le développement du sens de la mesure et l’acquisition de certaines habiletés essentielles en mesure (celles-ci seront abordées dans la section Habiletés mathématiques).
Chez quelques élèves, le sens de la mesure semble inné, comme s’il s’agit d’un talent légué à la naissance. Cependant, les recherches montrent que les élèves peuvent développer ce sens au moyen d’activités qui intègrent la manipulation de matériel concret et l’utilisation d’unités de mesure non conventionnelles et conventionnelles. Le développement du sens de la mesure dépasse l’apprentissage d’habiletés et de procédures relatives à l’acte de mesurer. Il constitue un cheminement structuré et organisé qui évolue et qui doit être adapté aux divers attributs mesurables d’un objet.
Buys et de Moor (2005, p. 29) soulignent que le but premier de l’enseignement en mesure est de développer le sens de la mesure et que pour atteindre ce but, le personnel enseignant doit amener les élèves :
- à reconnaître des situations quotidiennes qui font appel à la mesure;
- à développer l’habileté à distinguer les différents attributs mesurables d’un objet et à déterminer les situations dans lesquelles les appliquer;
- à visualiser les diverses unités de mesure liées aux différents attributs;
- à employer correctement le vocabulaire relatif à la mesure.
L’élève qui a le sens de la mesure est donc capable, par exemple, d’estimer et de déterminer la longueur d’un objet en le comparant avec un autre objet de longueur déterminée ou avec une certaine unité de mesure conventionnelle. Pour bien cerner la portée du sens de la mesure dans le processus de développement d’une compréhension des concepts, des relations et des procédures en mesure, il importe de s’attarder aux trois éléments suivants :
- le sens de l’espace;
- les repères;
- l’estimation.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 7-8.
Sens de la mesure
« La mesure est souvent considérée comme la détermination de la grandeur, de la quantité ou le degré de quelque chose en utilisant un instrument gradué en unités conventionnelles. Une définition plus large de la mesure inclut la comparaison de cette chose avec un objet de grandeur connue, l’estimation de son étendue, sa qualité, sa valeur ou son effet et son évaluation fondée sur une comparaison avec une norme quelconque. »
(Dougherty et Venenciano, 2007, p. 452, traduction libre).
Aperçu du Sens de la mesure
Les contenus d’apprentissage de l’attente E2 (Sens de la mesure) font appel à un grand nombre de concepts. Afin d’aider le personnel enseignant à planifier et à mettre en œuvre des stratégies qui offrent un enseignement efficace et cohérent dans cette attente, les concepts clés sont regroupés sous une seule grande idée, soit le sens de la mesure. Cette grande idée est présentée et développée en fonction de trois énoncés qui la sous-tendent : attributs et concepts fondamentaux, relations et acte de mesurer.
Grande idée – Sens de la mesure
L’exploration de divers attributs, de relations ainsi que de procédures liées à l’acte de mesurer permet de développer le sens de la mesure.
Énoncé 1 – Attributs et concepts fondamentaux
La compréhension des attributs en mesure et des concepts fondamentaux qui les sous-tendent donne un sens aux unités de mesure et à l’acte de mesurer.
Énoncé 2 – Relations
La compréhension des diverses relations en mesure facilite la formulation de conjectures et de généralisations.
Énoncé 3 – Acte de mesurer
La compréhension des procédures nécessite de s’approprier toutes les étapes de l’acte de mesurer afin de consolider les concepts en mesure.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 35-36.
Habileté à visualiser
« L’habileté à visualiser est un processus qui permet à l’élève de se représenter des concepts abstraits sous forme d’images mentales. Ces images lui permettent de manipuler les concepts, de les rendre signifiants et de se les approprier. »
(Small, 2006, p. 132, traduction libre).
L’habileté à visualiser correspond à la capacité de se faire une image mentale d’une situation ou d’un concept abstrait. En mesure, cette habileté est liée principalement à la capacité de se faire une image mentale :
- de certains attributs mesurables;
- de repères associés aux divers attributs.
Visualiser certains attributs mesurables : La capacité de se faire une image mentale de certains attributs mesurables aide les élèves à mieux en comprendre le sens. Au cycle moyen, les élèves doivent développer l’habileté à visualiser les attributs longueur, aire, capacité et angle. En ce qui a trait aux attributs temps et masse, puisqu’ils ne représentent pas quelque chose qu’il est possible de voir ou d’illustrer, les élèves peuvent au mieux se faire une image mentale de quelques repères appropriés.
Pour l’attribut longueur, les élèves doivent visualiser un espace à une dimension, c’est-à-dire se faire une image mentale d’une ligne droite ou courbe. Par exemple, dans une situation où il est question de déterminer la longueur d’un prisme rectangulaire, elles et ils doivent visualiser qu’il s’agit de déterminer la mesure de l’espace entre les extrémités gauches et droites du prisme.
Les élèves doivent aussi reconnaître que, dans certaines situations, l’attribut longueur peut prendre un autre nom, par exemple :
- la hauteur d’une montagne;
- la largeur d’un prisme;
- l’épaisseur d’un gâteau;
- la taille d’une personne;
- la profondeur d’un lac;
- le diamètre d’une roue;
- le périmètre d’une boîte;
- la circonférence d’un verre.
Pour l’attribut aire, les élèves doivent visualiser un espace à deux dimensions, c’est-à-dire se faire une image mentale d’une surface plane ou courbe. Par exemple, dans une situation où il est question de déterminer l’aire d’une des faces d’un prisme rectangulaire, elles et ils doivent visualiser qu’il s’agit de déterminer la mesure de l’espace occupé par la surface de cette face.
Les élèves doivent aussi reconnaître que, dans certaines situations, l’attribut aire peut prendre un autre nom, par exemple :
- l’étendue d’un terrain;
- la superficie d’une ville.
Pour l’attribut capacité, les élèves doivent visualiser un espace à trois dimensions, c’est-à-dire se faire une image de l’espace intérieur d’un contenant. Par exemple, dans une situation où il est question de déterminer la capacité d’un prisme, elles et ils doivent visualiser qu’il s’agit de déterminer la mesure de son espace intérieur.
Pour l’attribut angle, les élèves doivent d’abord se faire une image mentale de l’intersection de deux demi-droites ou de deux demi-plans, puis visualiser l’inclinaison que les « côtés » de l’angle ont l’un par rapport à l’autre. L’écart entre ces côtés correspond à la mesure de l’angle.
Visualiser des repères : La capacité de se faire une image mentale de certains repères associés aux attributs mesurables aide les élèves à estimer la grandeur d’un attribut ou à vérifier la vraisemblance d’un résultat obtenu à la suite de l’utilisation d’un instrument de mesure ou de l’application d’une formule. Par exemple, l’élève qui a retenu la largeur d’une porte comme repère pour représenter une mesure de 1 m peut l’utiliser pour estimer que la longueur du pupitre de l’enseignante ou de l’enseignant mesure environ 1,5 m.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 20-22.
Au cycle moyen, les élèves poursuivent l’étude des propriétés des figures planes et des solides au moyen d’activités de construction (par exemple, construction avec un géoplan, des pailles, de la pâte à modeler, du carton, des cubes emboîtables) et de représentation sur papier (par exemple, représentation sur du papier quadrillé, du papier à points).
Ces activités aident les élèves à se construire une représentation mentale des figures planes et des solides fondée sur des propriétés précises et favorisent le développement d’habiletés liées à la visualisation.
Les activités de manipulation avec du matériel concret et de construction avec le géoplan sont particulièrement utiles à cet effet. Comme pour les angles, il est nécessaire que le personnel enseignant représente ces figures planes de diverses façons afin que les élèves n’en développent pas une représentation mentale unique.
Par exemple, les élèves doivent reconnaître que chacune des figures planes ci-dessous représente un trapèze.

Afin de se construire une bonne représentation mentale des solides, les élèves doivent être en mesure de les visualiser aussi bien dans l’espace bidimensionnel des figures planes que dans l’espace tridimensionnel des solides.
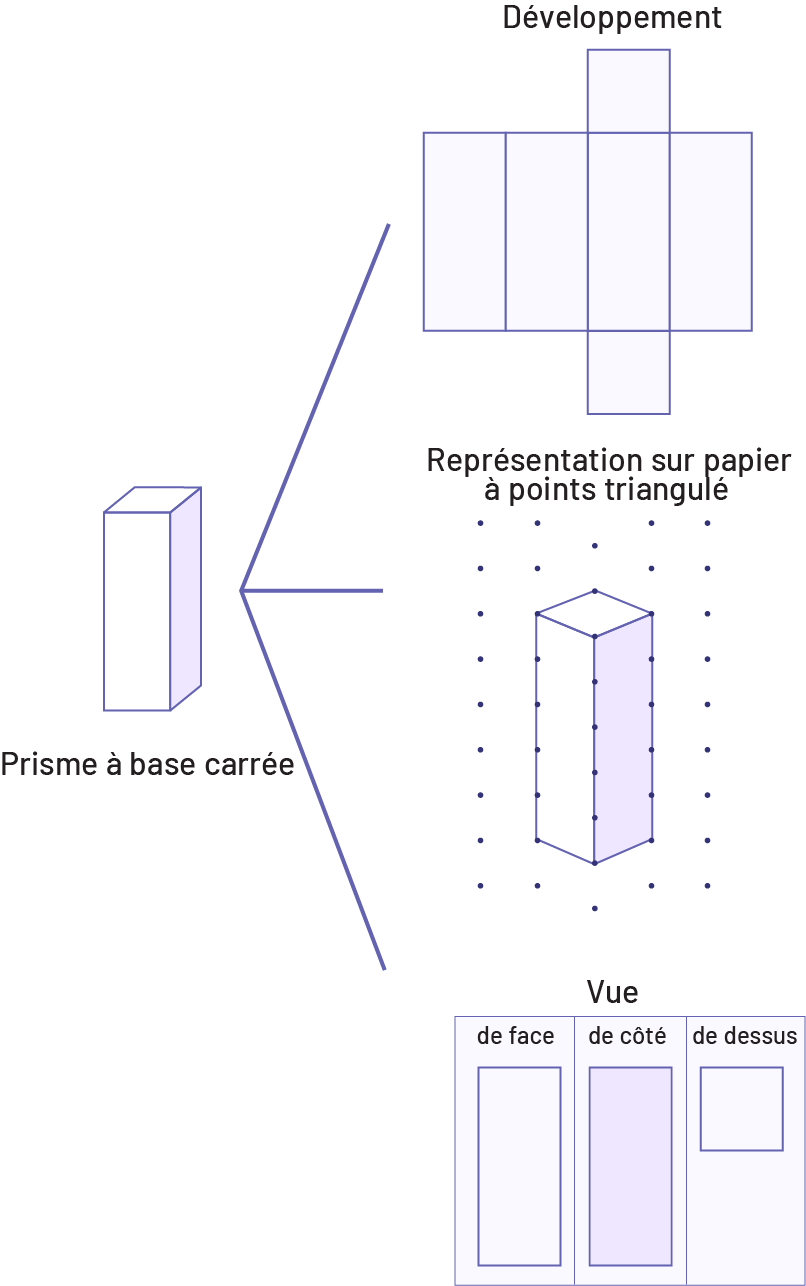
Pour les aider à développer l’habileté à passer d’un espace à l’autre et à consolider leurs connaissances des propriétés des solides, le personnel enseignant peut avoir recours à diverses activités de construction (par exemple, construire un modèle à l’aide de cubes, construire la coquille d’un solide à partir d’un développement donné) et à diverses activités de représentation (par exemple, tracer le développement d’un solide, associer un solide à son développement ou à ses vues de face, de côté et de dessus).
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 28-30.
La visualisation spatiale est un type particulier de pensée spatiale qui implique l’utilisation de notre imagination pour « générer, mémoriser, extraire et transformer des images visuelles bien structurées » (Lohman, 1996, traduction libre, p. 98); elle est parfois considérée comme étant la capacité à penser avec l’« intelligence de l’œil ».
(Ministère de l’Éducation de l’Ontario, 2014, p. 10).
La visualisation spatiale se développe en mobilisant certaines habiletés spatiales qu’a énumérées John Del Grande (1990), y compris la rotation mentale.
| HABILETÉS SPATIALES RELATIVES À LA VISUALISATION SPATIALE | DESCRIPTION |
| 1. Coordination oculomotrice | Habileté à coordonner la vue et les mouvements du corps. |
| 2. Perception de plans (forme et fond) | Habileté à percevoir un élément précis figurant sur une toile de fond complexe (intersections, superpositions). |
| 3. Constance des formes | Habileté à reconnaître des figures géométriques indépendamment de leur taille, de leur couleur et de leur orientation dans l’espace. |
| 4. Perception des positions | Habileté à percevoir la position d’un objet par rapport à soi. Habileté à discriminer des objets identiques, peu importe leur orientation. |
| 5. Perception des relations spatiales | Habileté à percevoir la position d’au moins deux objets par rapport à soi ou d’un objet par rapport à l’autre. |
| 6. Discrimination visuelle | Habileté à remarquer les ressemblances et les différences entre deux ou plusieurs objets. |
| 7. Rotation mentale | Habileté à « […] faire tourner mentalement des objets bidimensionnels ou tridimensionnels » (Ministère de l’Éducation de l’Ontario, 2014, p. 13). |
(John Del Grande, 1990. © 2019, National Council of Teachers of Mathematics. The Arithmetic Teacher, vol. 37, no 6.)
Source : Guide d'enseignement efficace des mathématiques de la 7e à la 10e année, p. 12-13.
Habileté à résoudre une situation-problème
L’habileté à résoudre des problèmes est un processus essentiel dans l’apprentissage de la mesure. Afin d’aider les élèves à développer cette habileté, le personnel enseignant doit leur présenter divers types de situations-problèmes dont le contexte est signifiant. Il doit les inciter à faire appel à leurs connaissances antérieures ainsi qu’à leurs stratégies en littératie et en résolution de problèmes, à communiquer clairement leurs résultats et à discuter des idées de leurs pairs lors d’échanges mathématiques. En étant ainsi engagées et engagés de manière optimale dans une réflexion portant sur les concepts visés, les élèves en clarifient le sens.
Les situations-problèmes en mesure doivent contribuer à améliorer la compréhension des élèves en ce qui a trait aux attributs et aux concepts fondamentaux, aux relations et à l’acte de mesurer. Il est essentiel que les élèves participent activement à la résolution des problèmes et aux discussions qui s’ensuivent. Ces expériences variées leur permettent de développer leur sens de la mesure.
Exemple
Remettre aux élèves un petit carton mesurant 1 cm2 ainsi qu’une copie des rectangles ci-dessous. Leur demander de déterminer, à l’aide du carré, les rectangles qui ont la même aire.
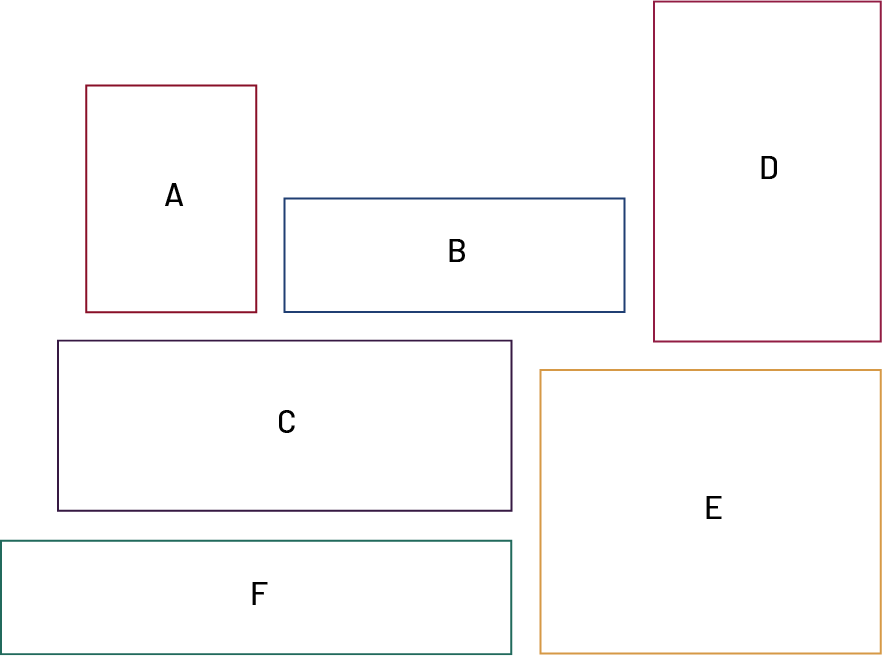
Lors de l’échange mathématique, le personnel enseignant incite les élèves à justifier leur réponse en posant des questions telles que :
- Quelle stratégie avez-vous utilisée pour déterminer que les rectangles C et D ont la même aire? (J’ai utilisé le petit carton comme unité de mesure. J’ai aligné ce carton 8 fois d’un côté du rectangle C et 3 fois de l’autre côté. Pour le couvrir complètement, il faudrait donc 8 colonnes de 3 cartons. Pour le rectangle D, j’ai trouvé qu’il faudrait 4 colonnes de 6 cartons. Dans les deux cas, il faudrait 24 cartons pour recouvrir les rectangles. Leur aire doit donc être la même.)
- Pouvez-vous penser à une autre façon de montrer que l’aire de ces deux rectangles est la même? (Si on découpe verticalement le rectangle C en son milieu et qu’on place les deux moitiés sur le rectangle D, on constate que le rectangle D est complètement recouvert. Cela prouve que l’aire des deux rectangles est la même.)
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 23-24.
Habileté à raisonner
Raisonner constitue un processus mental selon lequel des idées s’enchaînent de façon logique. Il s’agit d’une habileté importante puisqu’elle permet aux élèves de structurer leur pensée en intégrant un ensemble de connaissances et en établissant des relations entre elles. En mesure, les relations à établir sont nombreuses (par exemple, relations entre les attributs, relations entre les unités de mesure). L’habileté à raisonner dans un contexte de mesure permet aux élèves d’analyser les ressemblances et les différences entre les attributs mesurables, de tirer des conclusions et, ultimement, de réinvestir ces acquis dans un nouveau contexte ou dans une nouvelle situation. En leur demandant de justifier leur raisonnement et d’expliquer leur démarche de résolution de problèmes, le personnel enseignant profite de leur curiosité intellectuelle pour les amener à aller au-delà de la simple réponse et à réfléchir aux concepts fondamentaux propres à chaque attribut. Pour ce faire, il importe que le milieu d’apprentissage soit propice aux échanges mathématiques et fasse en sorte que les élèves se sentent à l’aise de formuler des conjectures et de les justifier.
Pour aider les élèves à acquérir l’habileté à raisonner en mesure, le personnel enseignant doit poser des questions ouvertes et proposer des situations-problèmes variées et complexes. Il doit les encourager :
- à représenter concrètement leur raisonnement en laissant des traces;
- à expliquer leur démarche et à justifier leur résultat;
- à observer et à analyser les stratégies utilisées par les autres élèves.
Exemple
Le personnel enseignant présente la situation suivante:
Marilou fait une randonnée pédestre de 3 km le long d’un sentier. Elle la commence à 9 h 42 et la termine à 11 h. En combien de temps a-t-elle fait la randonnée?
Pour aider les élèves à développer l’habileté à raisonner, il pose des questions telles que :
- Tu dis qu’elle a fait la randonnée en 78 minutes. Peux-tu justifier ta réponse?
- Quelle démarche as-tu utilisée?
- Comment cette démarche est-elle différente de celle présentée par l’élève précédente ou précédent?
- Quelle démarche semble plus efficace? Pourquoi?
Le personnel enseignant a parfois tendance à demander aux élèves de justifier leur réponse seulement lorsque celle-ci est erronée. Par conséquent, lorsqu’on leur demande de justifier un résultat, les élèves sont portées et portés à croire qu’elles et ils ont commis une erreur. Il importe donc de les inciter régulièrement à justifier leur réponse, qu’elle soit correcte ou pas. Ainsi, les élèves saisiront qu’il s’agit là simplement d’une étape inhérente à tout raisonnement.
Le questionnement du personnel enseignant et les suggestions des pairs lors de l’échange mathématique peuvent aider les élèves :
- à réaliser qu’il est possible de résoudre la situation-problème donnée de façon plus simple;
- à formuler leur raisonnement;
- à émettre des conjectures et des généralisations plus complexes.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 25-26.
La nature du raisonnement mathématique des élèves est étroitement liée à leur capacité d’abstraction. Aux niveaux 0 et 1, les élèves utilisent surtout un raisonnement mathématique de type inductif, c’est-à-dire un raisonnement qui va du particulier au général. Ainsi, lorsqu’elles et ils manipulent un nombre limité de formes géométriques semblables et qu’elles et ils en observent les attributs ou les propriétés, elles et ils attribuent ces caractéristiques à l’ensemble des formes géométriques qui font partie de la même famille. Par exemple, après avoir manipulé un petit nombre d’objets de forme pyramidale, les élèves peuvent conclure que toutes les pyramides ont une extrémité pointue.
Au cycle moyen, les élèves passent progressivement d’un raisonnement inductif à un raisonnement déductif informel, c’est-à-dire un raisonnement qui va du général au particulier. Ce type de raisonnement leur permet de tirer certaines conclusions au sujet d’une forme géométrique quelconque à partir de propriétés connues. Par exemple, après avoir reconnu que lorsqu’on trace une des deux diagonales d’un rectangle, on obtient deux triangles congruents, les élèves peuvent déduire que l’aire de chacun de ces triangles est égale à la moitié de l’aire du rectangle (voir la figure ci-dessous).
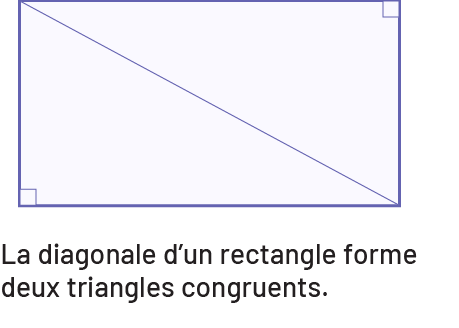
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 36.
Habileté à communiquer
« En effet, c’est en examinant les stratégies et les idées proposées par d’autres que les élèves développent une pensée critique et parviennent à reconnaître et à dégager les forces et les limites d’un argument mathématique. Ce faisant, ils peuvent aussi apprécier la valeur d’un langage mathématique clair, juste et efficace. »
(Ministère de l’Éducation de l’Ontario, 2006a, fascicule 2, p. 81).
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 27.
La communication est un élément essentiel à l’apprentissage des mathématiques. C’est une habileté qui va au-delà de l’utilisation appropriée de la terminologie et des symboles mathématiques dans une communication verbale ou écrite. C’est aussi, de façon plus importante, un véhicule par lequel les élèves acquièrent une compréhension des concepts mathématiques dans des contextes qui font appel à des raisonnements et à des arguments mathématiques. C’est ce que Radford et Demers (2004) appellent la dimension conceptuelle de la communication.
Ces chercheurs soulignent aussi l’importance de prendre en compte la dimension sociale de la communication. En effet, qui dit « communication » dit « échange » entre deux personnes ou plus. L’échange sera profitable pour toutes les personnes impliquées dans la mesure où il règne au sein du groupe un climat d’engagement au dialogue et une culture de respect et d’écoute par rapport aux propos des autres.
Pour accroître l’efficacité de l’enseignement de la géométrie dans sa salle de classe, le personnel enseignant doit favoriser l’émergence d’une culture qui valorise la communication comme moyen d’appropriation du savoir. Il doit aussi fournir aux élèves de multiples occasions de discuter de leurs hypothèses avec leurs pairs et de formuler un argument mathématique clair et convaincant.
image Infographie nommée : communication.Quatre personnes sont assises à une table. Elles sont assises chacune à un coin d’une table en losange. En haut à gauche on peut lire : dimension sociale. En haut à droite on peut lire : dimension conceptuelle. Les personnes qui sont face à face sont reliées par une ligne bleue. Cela divise la table en 4 parties. Les parties représentent une idée : syntaxe et symboles; arguments mathématiques; considération des propos des autres ; engagement au dialogue.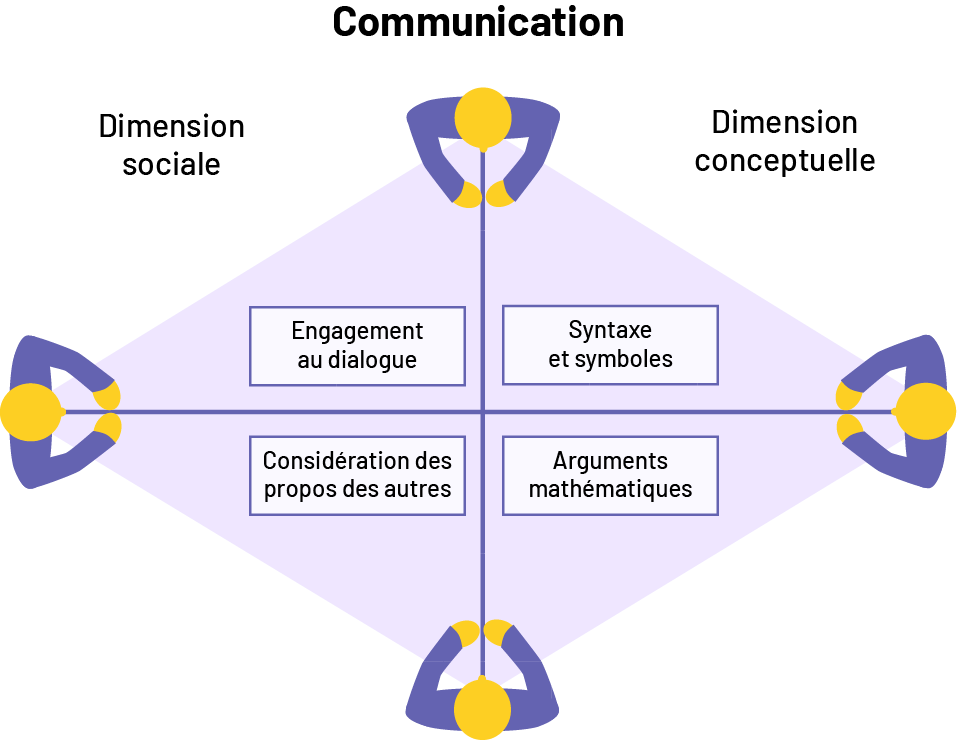
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 8-9.
La capacité des élèves à présenter un argument mathématique reflète aussi leur niveau de pensée. Selon Radford et Demers (2004), les élèves du cycle primaire commencent à être capables de présenter un argument mathématique en utilisant des termes de causalité tels que alors, car ou parce que. Par contre, comme elles et ils n’ont pas toujours bien compris la notion de causalité, elles et ils utilisent parfois ces termes incorrectement pour justifier une conclusion ou la solution à un problème (par exemple, « C’est un carré parce que ça ressemble à un carré. »). Le personnel enseignant peut aider les élèves à développer l’habileté à utiliser les termes de causalité en leur donnant l’occasion de réagir de façon critique aux arguments présentés par d’autres élèves (par exemple, « Matéo dit que c’est un carré parce que ça ressemble à un carré. Selon vous, est-ce que c’est un argument clair et convaincant? »).
Au cycle moyen, les élèves peuvent davantage présenter un argument mathématique en utilisant correctement les termes de causalité (par exemple, « La figure est un carré parce qu’elle a quatre côtés congrus et quatre angles droits. »). Elles et ils commencent aussi à employer les termes de conséquence logique tels que si... alors ou puisque... donc (par exemple, « Puisque tout quadrilatère qui a quatre angles droits est un rectangle et que tous les carrés ont quatre angles droits, donc tous les carrés sont des rectangles. »). Même si les élèves ne sont pas encore en mesure de présenter une preuve formelle et rigoureuse, elles et ils peuvent apprécier la logique d’un bon argument mathématique.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 37.
Pour qu’il y ait communication, il est nécessaire d’avoir une intention, une situation, un contexte, un code, un message et une interaction explicite ou implicite entre des personnes.
L’habileté à communiquer en mesure se développe surtout dans le contexte d’une résolution de problèmes ou d’un échange mathématique. Dans toute situation qui fait appel au raisonnement et à un argument mathématique, l’habileté à communiquer permet aux élèves de développer leur compréhension des concepts. La dimension sociale de la communication joue un rôle important dans l’acquisition de cette habileté et elle profite à toutes les personnes engagées dans l’acte de mesurer. Aux cycles primaire et moyen, la communication orale est un préalable à la communication écrite.
Communication orale
La communication orale est la plus naturelle des formes d’expression utilisées par les élèves. La parole reste le moyen le plus utile et le plus fréquent de communiquer au quotidien. Elle est essentielle à la transmission d’idées, de découvertes, de démarches et de résultats en mesure. Elle sert de levier à la réflexion des élèves et elle les engage dans un dialogue structuré qui les aide à donner du sens à leurs explorations. Afin que les élèves développent cette habileté, il faut leur fournir diverses occasions de s’exprimer et de montrer leur compréhension des différents concepts.
Au cycle moyen, lors des situations d’apprentissage en équipe et des échanges mathématiques, les élèves doivent apprendre à utiliser un vocabulaire relatif aux attributs et aux unités de mesure conventionnelles. Elles et ils doivent comparer des objets entre eux en utilisant une terminologie appropriée (par exemple, à la même capacité, à une masse plus grande que) et décrire la mesure à l’aide de termes justes et exacts. Les élèves diront, par exemple, que « le périmètre du carré de sable est de 12 m et celui de l’espace de jeu est de 24 m ». Le personnel enseignant doit parfois guider les élèves dans l’utilisation d’un vocabulaire juste. Par exemple, si une ou un élève dit : « mon livre est plus gros que le tien », le personnel enseignant doit l’inciter à préciser sa pensée en lui demandant si son livre est plus épais, plus long ou plus large que celui de son amie ou ami.
Afin de promouvoir la communication orale entre les élèves, le personnel enseignant doit réduire la durée et la fréquence de ses interventions, et laisser la place aux échanges et aux analyses des idées émises par les équipes ou les individus. Avant de solliciter une réponse à une question, il doit encourager les discussions de groupe et allouer un temps de réflexion suffisant. Le Guide d'enseignement efficace des mathématiques de la maternelle à la 6e année, fascicule 2 (Ministère de l’Éducation de l’Ontario, 2006a, p. 87-95), propose diverses stratégies favorisant la communication orale en mathématiques.
Conjointement à la parole, les actions posées par les élèves peuvent contribuer à la communication en montrant la stratégie utilisée pour résoudre un problème ou la compréhension d’un concept en mesure.
Exemple
Deux élèves montrent la façon dont elles utilisent une éprouvette graduée pour déterminer le contenant parmi trois qui a la plus petite capacité.
Communication écrite
La communication écrite est un excellent moyen pour les élèves de clarifier leurs idées et de décrire leurs stratégies de résolution de problèmes. Par le fait même, elle constitue une bonne indication des apprentissages réalisés. En effet, les élèves révèlent souvent une part importante de ce qu’elles et ils ont appris et maîtrisé par les traces laissées sur leur feuille de travail. Le personnel enseignant doit les encourager à laisser le plus de traces possible.
Exemple
Le personnel enseignant présente aux élèves le problème suivant.
Monsieur Brûlé dispose de 24 m de ruban-cache pour délimiter un espace de jeu rectangulaire sur le plancher du gymnase. Il se rend compte qu’il pourrait construire plusieurs rectangles différents. Il décide alors de tracer certains des rectangles sur du papier quadrillé en utilisant une échelle selon laquelle 1 cm représente 1 m. Dessinez quelques-uns des rectangles que monsieur Brûlé pourrait tracer en vous assurant que le périmètre de chacun mesure 24 cm. Déterminez ensuite l’aire de chaque rectangle. Laissez des traces de votre travail.
Quelques élèves laissent des traces de leur pensée mathématique à l’aide de dessins seulement. Il importe de les amener à montrer leur compréhension et leurs apprentissages à l’aide de mots, d’expressions et de phrases afin que les traces deviennent organisées, claires et précises.
Pour aider les élèves à améliorer la présentation de leur solution écrite, le personnel enseignant doit les encourager à discuter de la tâche à accomplir, à anticiper les solutions possibles et à recourir à du matériel concret et à des symboles familiers. Plusieurs outils favorisent l’amélioration de la communication écrite (par exemple, mur de mots, outil organisationnel, journal de mathématiques, tableau interactif).
En résumé, la communication écrite permet aux élèves :
- de consigner leurs apprentissages et de situer l’évolution de leur pensée mathématique dans un portfolio ou un journal de mathématiques;
- de prendre le temps de réfléchir et de s’organiser;
- de faire une objectivation relative à certains concepts;
- de profiter d’un espace d’expression personnel.
Elle permet aussi au personnel enseignant d’évaluer chez les élèves la compréhension des concepts et de mieux planifier les prochaines activités d’apprentissage. Le Guide d'enseignement efficace des mathématiques de la maternelle à la 6e année, fascicule 2 (Ministère de l’Éducation de l’Ontario, 2006a, p. 97-109) propose diverses stratégies favorisant la communication écrite en mathématiques.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 27-31.
Habileté à abstraire
Au cycle primaire, la pensée géométrique des élèves se situe généralement aux niveaux 0 et 1. Au début, les élèves apprennent à reconnaître les formes géométriques, à les nommer et à énumérer certains de leurs attributs physiques (par exemple, la sphère est ronde et elle roule). Plusieurs se construisent alors une représentation mentale des formes géométriques en les associant à des objets connus (par exemple, un rectangle ressemble à une porte, une sphère ressemble à un ballon). Dans certains cas, cette représentation est tellement ancrée qu’elle les empêche de concevoir une orientation de la forme autre que celle qui correspond à la représentation qu’elles et ils en ont. Voir les figures ci-dessous.
 image Les élèves associent un rectangle à un objet connu, par exemple, une porte. Le texte est accompagné du dessin d’un rectangle et de son angle droit.Cette figure ne correspond pas à l’image que se font certaines et certains jeunes élèves. Le texte est accompagné du dessin d’un rectangle et son angle droit dans une posture oblique.
image Les élèves associent un rectangle à un objet connu, par exemple, une porte. Le texte est accompagné du dessin d’un rectangle et de son angle droit.Cette figure ne correspond pas à l’image que se font certaines et certains jeunes élèves. Le texte est accompagné du dessin d’un rectangle et son angle droit dans une posture oblique.Par la suite, les élèves délaissent progressivement les références aux attributs physiques et aux objets connus au fur et à mesure qu’elles et ils apprennent à décrire les formes géométriques en fonction d’une liste de propriétés nécessaires (par exemple, un rectangle est une figure plane qui a quatre côtés, quatre angles droits et des côtés opposés qui sont congrus et parallèles).

Au cycle moyen, la pensée géométrique des élèves progresse vers le niveau 2 au fur et à mesure que leur capacité d’abstraction se développe. Cette capacité est liée à la faculté de concentrer son attention sur certaines propriétés de façon isolée. Elle leur permet, entre autres, de choisir parmi la liste de propriétés nécessaires d’une forme géométrique celles qui suffisent à la définir (propriétés suffisantes). Le personnel enseignant peut aider les élèves à développer cette faculté en leur proposant diverses situations d’apprentissage :
- Situations d’apprentissage qui font appel à une ou deux propriétés en particulier
Par exemple, le personnel enseignant peut demander aux élèves de construire sur un géoplan ou tracer sur du papier à points, un quadrilatère qui a quatre côtés congrus et au moins un angle droit. En comparant leurs résultats, les élèves constateront que toutes les figures obtenues sont des carrés et pourront conclure que pour définir un carré, il suffit de dire que c’est un quadrilatère qui a quatre côtés congrus et au moins un angle droit.
- Situations d’apprentissage impossibles à réaliser
Par exemple, le personnel enseignant peut demander aux élèves de construire sur un géoplan ou tracer sur du papier à points, un triangle qui a trois côtés congrus et un angle obtus. Ils constateront que c’est impossible et pourront conclure qu’un triangle équilatéral ne peut être obtusangle.
- Situations d’apprentissage qui exigent la considération simultanée de plus d’une forme géométrique
Par exemple, le personnel enseignant peut demander aux élèves de construire sur un géoplan ou tracer sur du papier à points, un quadrilatère qui est à la fois un losange et un rectangle. En tenant compte des propriétés de chacune des deux figures planes, les élèves constateront que la figure est nécessairement un carré et pourront conclure qu’il est possible de définir un carré comme étant un losange qui a quatre angles droits ou un rectangle qui a quatre côtés congrus. Ce type de situation permet aux élèves de classifier les formes géométriques de façon hiérarchique (Figures 17 et 18) afin de faire ressortir les relations d’inclusion (par exemple, tous les rectangles font partie de la famille des parallélogrammes, mais tous les parallélogrammes ne font pas partie de la famille des rectangles) et d’exclusion (par exemple, un triangle acutangle ne peut pas être obtusangle et vice versa).
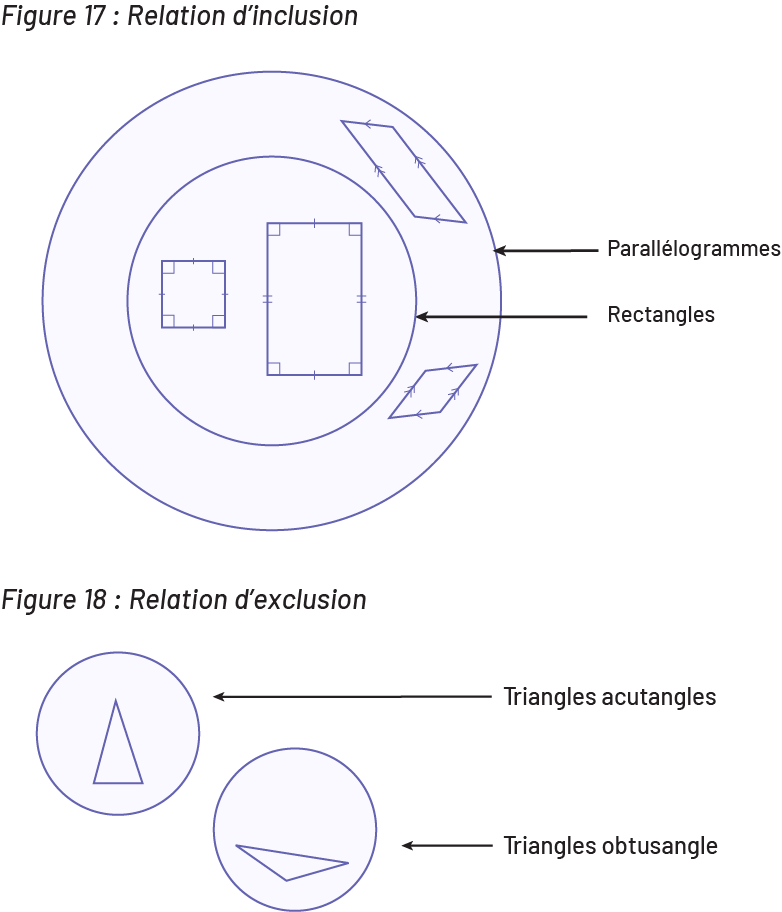 image Relation d’inclusion.Deux cercles, l’un est l’autre. Le plus grand représente l’ensemble des parallélogrammes, des exemples y sont dessinés. Le cercle plus petit est l’ensemble des rectangles.Relation d’exclusion :Deux cercles sont représentés, individuellement. Le premier représente les triangles acutangles, le deuxième représente les triangles obtusangles. Un exemple est placé dans chaque cercle.
image Relation d’inclusion.Deux cercles, l’un est l’autre. Le plus grand représente l’ensemble des parallélogrammes, des exemples y sont dessinés. Le cercle plus petit est l’ensemble des rectangles.Relation d’exclusion :Deux cercles sont représentés, individuellement. Le premier représente les triangles acutangles, le deuxième représente les triangles obtusangles. Un exemple est placé dans chaque cercle.Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 32-34.
Le personnel enseignant doit encourager les élèves à dépasser l’application des procédures et l’emploi d’instruments de mesure afin qu’elles et ils puissent développer une bonne compréhension conceptuelle des attributs en mesure, des unités conventionnelles correspondantes ainsi que des propriétés géométriques. Il doit aussi les inciter à établir des liens entre les concepts, les procédures et les relations en mesure ainsi qu’en géométrie.
Pour ce faire, le personnel enseignant doit :
- choisir des stratégies d’enseignement et d’apprentissage efficaces;
- choisir stratégiquement les pistes de questionnement;
- planifier et structurer l’échange mathématique;
- créer un milieu d’apprentissage propice au développement du sens de la mesure.
Choisir des stratégies d’enseignement et d’apprentissage efficaces : Une stratégie d’enseignement se définit comme une façon de faire, une approche, une série d’actions et de moyens que le personnel enseignant utilise dans un contexte donné. Un enseignement efficace en sens de l’espace amène les élèves :
- à réfléchir aux attributs et aux relations;
- à résoudre des problèmes de mesure et de géométrie, tant dans des contextes de la vie courante que dans des contextes purement mathématiques;
- à faire preuve de motivation et d’engagement dans la résolution de ces problèmes;
- à discuter de leurs essais, des solutions possibles et de leur compréhension des concepts et des procédures.
Choisir stratégiquement les pistes de questionnement : Afin d’aider les élèves à développer une pensée mathématique qui reflète le sens de l’espace, le personnel enseignant doit s’assurer que les questions qu’il leur pose sont adaptées au moment, à la situation et au degré de compréhension des élèves. Pour ce faire, il doit choisir des questions qui aident entre autres les élèves à approfondir la compréhension des concepts, établir des relations, à proposer des conjectures et à formuler des généralisations.
Planifier et structurer l’échange mathématique : Tout au long d’une situation d’apprentissage, le personnel enseignant planifie le déroulement de l’activité d’objectivation ou de l’échange mathématique. Pour ce faire, il observe attentivement les travaux des élèves et détermine, en fonction d’un ou de plusieurs objectifs, ceux qui devraient être présentés à l’ensemble de la classe. Ces travaux doivent susciter la discussion et aider les élèves à consolider leur compréhension des concepts visés.
La stratégie selon laquelle les travaux des élèves sont choisis et affichés dans la classe en fonction d’objectifs précis est parfois appelée stratégie du Bansho. Ainsi, les travaux des élèves peuvent être choisis et affichés afin de mettre en évidence et de comparer :
- les stratégies de résolution de problèmes utilisées par les élèves (par exemple, illustrer la diversité des stratégies utilisées ou illustrer la même stratégie présentée selon différents niveaux de structure et d’organisation);
- le matériel utilisé par les élèves (par exemple, illustrer la différence entre une représentation faite à l’aide de dessins et une représentation faite à l’aide d’une règle, d’une disposition rectangulaire ou de symboles);
- la clarté de la solution proposée (par exemple, illustrer la différence entre une représentation partielle d’une solution et une représentation dans laquelle les élèves ont organisé, montré et expliqué leur solution clairement à l’aide de mots et de symboles).
Pendant l’échange mathématique, le personnel enseignant doit structurer l’échange en dirigeant les discussions et en effectuant des interventions stratégiques. Il doit s’assurer de clarifier les concepts visés et de faire en sorte que les élèves les comprennent bien. Au besoin, il peut terminer l’échange mathématique par le modelage d’une démarche, d’une stratégie ou d’une procédure efficace. Ce modelage peut être fait soit par le personnel enseignant, soit par une équipe d’élèves. Un échange mathématique bien structuré permet aux élèves de consolider leurs connaissances et leur compréhension des concepts et des procédures, et de reconnaître l’importance d’une communication efficace.
Créer un milieu d’apprentissage propice au développement du sens de l'espace : Un milieu d’apprentissage propice au sens de l’espace est un environnement où l’on mise autant sur le développement de la compréhension conceptuelle des propriétés géométriques, des attributs et des unités de mesure que sur la compréhension des procédures. Le personnel enseignant doit consciemment utiliser, tant en mathématiques que dans les autres matières, diverses situations qui font appel à la mesure ainsi qu’à la géométrie. C’est en étant régulièrement confrontées et confrontés au besoin de mesurer et d’effectuer des expériences variées en géométrie dans toutes sortes de situations que les élèves comprennent l’importance de la mesure et de la géométrie et qu’elles et ils développent les habiletés requises pour les obtenir.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 31-34.
