À vue d'oeil...

F1.4 Déterminer la valeur croissante d’intérêts simples et composés à divers taux à l’aide d’outils technologiques, et expliquer l’incidence des intérêts dans la planification financière à long terme.

Habileté : déterminer la valeur croissante d’intérêts simples et composés à divers taux

---

Dans toute situation dans laquelle de l’intérêt est impliqué, il y a de l’argent prêté, et de l’argent emprunté, et la personne ou l’organisme qui emprunte l’argent devra remettre de l’intérêt en plus de la somme initiale prêtée. Il existe, cependant, plus d’une façon de calculer l’intérêt, chacune d’elles ayant des avantages et des désavantages. Les deux exemples qui suivent présentent des situations d’emprunt et de prêt, ainsi que la façon dont ces deux calculs d’intérêt peuvent être bénéfiques.

Exemple : intérêt simple 

L’emprunt pour l’achat d’une automobile : Lors de l’achat d’un véhicule avec emprunt, l’intérêt est calculé au départ et ajouté au montant principal, et ce montant est divisé par le nombre de paiements. Avec cette approche, les paiements ne tiennent pas compte des intérêts, peu importe la fréquence des paiements.

Par exemple, si une personne emprunte 1 000 $ à un taux d’intérêt annuel de 2 % pendant 5 ans, l’intérêt est calculé au début du terme et divisé par le nombre de paiements. La personne dépensera un total de 1 100 $, soit 1 000 $ pour le retour du prêt initial et 100 $ en intérêt (1 000 $ x 2 % = 20 $ et 20 $ x 5 = 100 $).

Puisque l’intérêt simple ne tient pas compte des intérêts accumulés, c’est-à-dire qu’il n’y a pas d’intérêt calculé sur l’intérêt, l’intérêt simple présente un avantage par rapport à l’intérêt composé pour la personne ou l’organisme qui emprunte l’argent (si les taux sont comparables).

Exemple : intérêt composé 

Les certificats de placement garanti (CPG) : Un CPG est un produit financier qui ressemble à un prêt à une institution financière de la part d’un client. Le client s’engage à ne pas avoir accès à une somme d’argent en échange d’un taux d’intérêt plus élevé que d’habitude. L’intérêt est déposé dans le compte actuel, contribuant au solde du compte. Ce montant est donc inclus dans le calcul d’intérêt lors du prochain versement. L’investissement principal et les intérêts composés sont versés au client à la fin du terme (la maturité).

Par exemple, si le client s’engage à investir 1 000 $ dans un CPG à un taux d’intérêt annuel de 2 % pendant 5 ans, l’intérêt est toujours calculé à partir du solde du compte. La valeur du compte suit alors le tableau suivant :

Puisque l’intérêt est calculé sur l’intérêt remis, l’intérêt composé présente un avantage pour la personne qui prête l’argent par rapport à l’intérêt simple (si on compare deux situations dans lesquelles les taux d’intérêt sont comparables).

Ces exemples pourraient être modélisés pour le groupe-classe en projetant ou en faisant un partage d’écran d’un outil en ligne de calcul d’intérêt. Il en existe plusieurs. Par la suite, les élèves peuvent utiliser leurs propres objectifs financiers à titre d’inspiration pour explorer les outils en ligne et voir l’effet du montant, de la durée et du taux d’intérêt sur la valeur d’un prêt ou d’un investissement.

Pour aller plus loin : L’intérêt composé peut être représenté par une relation exponentielle, telle que représentée par ce diagramme :

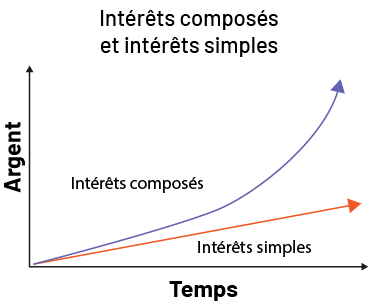
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1^re à la 8^e année, 2020, Ministère de l’Éducation de l’Ontario.

Sans présenter la formule actuelle de l’intérêt composé, qui est quand même assez complexe, l’utilisation du matériel de manipulation ou d’outils technologiques afin de créer un diagramme comme celui-ci peut démontrer la croissance d’un investissement ou la valeur d’un prêt en utilisant les deux façons de calculer l’intérêt.

Exemple : intérêt composé (relation exponentielle)

Exemple : intérêt simple (relation linéaire)

Connaissance : emprunt

---

Un emprunt est de l’argent que quelqu’un a reçu d’un autre parti conformément à un accord prévoyant son remboursement. La plupart des fonds empruntés sont remboursés avec de l’intérêt.

Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1^re à la 8^e année, 2020, Ministère de l'Éducation de l'Ontario.

Connaissance : intérêts simples

---

Les intérêts simples sont toujours calculés sur le même montant, c’est-à-dire en fonction du montant initial.

Exemple

5 000 $ placés à un taux annuel de 6 %; intérêts payés à la fin de la période de 3 ans :

Connaissance : intérêts composés

---

Les intérêts calculés à partir du capital initial du dépôt ou du prêt, qui tient compte de tous les intérêts cumulés des périodes précédentes. Les intérêts composés peuvent être calculés selon n’importe quel calendrier, soit en continu, quotidiennement ou annuellement.

Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1^re à la 8^e année, 2020, Ministère de l'Éducation de l'Ontario.

Exemple

5 000 $ placés à un taux annuel de 6 %; intérêts composés sur 3 ans :

Connaissance : prêt

---

Remise temporaire d’une chose par quelqu’un (le prêteur) à quelqu’un d’autre (l’emprunteur) à condition que ce dernier la restitue après s’en être servi. Par exemple, un prêteur peut fournir des fonds à un emprunteur pour une hypothèque, l’achat d’une automobile ou le financement d’une entreprise.

Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1^re à la 8^e année, 2020, Ministère de l'Éducation de l'Ontario.