B2.5 représenter et résoudre des problèmes de groupes égaux dont le nombre d’éléments est égal ou inférieur à 10, y compris des problèmes dans lesquels chaque groupe est la moitié d’un tout, à l’aide d’outils et de schémas.
Activité 1 : résolution de problèmes de groupement
À la suite d’une sortie au verger, l’enseignante veut remettre la moitié d’une pomme à chacun des huit enfants. De combien de pommes a-t-elle besoin?
STRATÉGIE
Utilisation d’un schéma pour représenter le problème
Je dessine 8 bonshommes. Je divise une pomme en 2 parties égales. J’ai maintenant 2 moitiés. Je place 1 moitié sous le premier bonhomme et 1 autre moitié sous le deuxième bonhomme. J’ai donc besoin de 1 pomme pour 2 personnes. Je dessine 1 moitié de pomme sous chacun des 6 autres bonshommes. Donc, je vois qu’il y a 8 moitiés partagées entre 8 personnes. Alors, l’enseignante a besoin de 4 pommes pour 8 enfants.
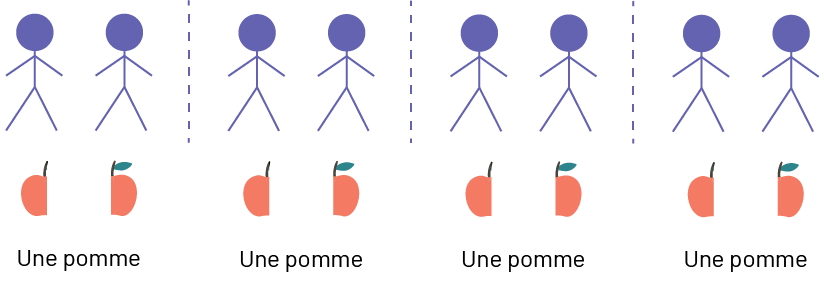
Source : adapté de En avant, les maths!, 1re, CM, Nombres, p. 3.
Activité 2 : résolution de problèmes de groupement
Des élèves cherchent leurs mitaines dans le panier. Il y a 10 mitaines dans le panier. Combien d’élèves y a-t-il?
STRATÉGIE
Utilisation d’un Rekenrek pour représenter le problème
J’utilise un Rekenrek pour représenter ce problème. Je sais que chaque élève doit avoir deux mitaines. Je déplace 2 perles vers la gauche sur la première tige. Je déplace 2 autres perles à la gauche sur la tige suivante. J’ai maintenant 4 perles. En comptant par intervalles de 2, je continue à déplacer 2 perles par tige jusqu’à ce que j’aie atteint 10, soit 2-4-6-8-10 mitaines. Je compte le nombre de rangées de 2 perles, et il y en a 5. Alors, je sais qu’il y a 5 élèves qui cherchent leurs mitaines dans le panier.
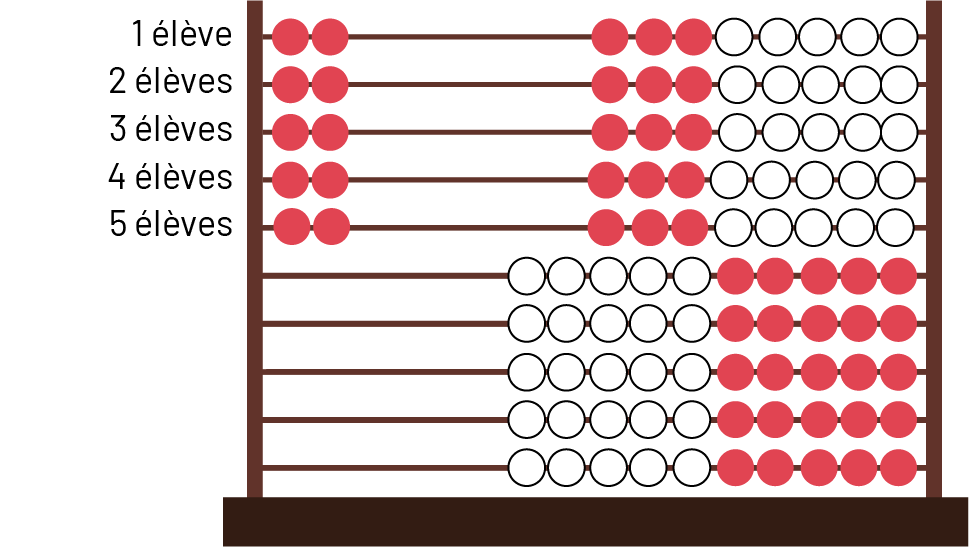 image Voici l’illustration d’un Rekenrek muni de dix tiges, chacune munies de cinq perles rouges et cinq perles blanches.Sur les cinq premières tiges, deux perles rouges sont entassées à gauche, tandis que les huit autres perles sont entassées à droite. À gauche de la première tige, il est écrit « un élève ». À gauche de la deuxième tige, il est écrit « deux élèves », et ainsi de suite jusqu’à cinq élèves. De la sixième à la dixième tige, toutes les perles sont entassées à droite.
image Voici l’illustration d’un Rekenrek muni de dix tiges, chacune munies de cinq perles rouges et cinq perles blanches.Sur les cinq premières tiges, deux perles rouges sont entassées à gauche, tandis que les huit autres perles sont entassées à droite. À gauche de la première tige, il est écrit « un élève ». À gauche de la deuxième tige, il est écrit « deux élèves », et ainsi de suite jusqu’à cinq élèves. De la sixième à la dixième tige, toutes les perles sont entassées à droite.
Source : adapté de En avant, les maths!, 1re, CM, Nombres, p. 4.
