B1.1 Lire et représenter les nombres naturels de 0 jusqu’à 50 et décrire les façons dont ils sont utilisés dans la vie quotidienne.
Habileté : lire les nombres naturels
La lecture des nombres aide à les interpréter comme des quantités lorsqu’ils sont exprimés en mots ou en chiffres, ou représentés à l’aide de matériel concret ou de modèles.
Une quantité décrit un ordre de grandeur (le « nombre de » ou le « combien y a-t-il de ») et constitue un concept essentiel au développement du sens du nombre.
Lorsque les très jeunes enfants apprennent à compter, elles et ils ne font pas immédiatement de liens entre les nombres récités et la notion de quantité. Ensuite, lorsque les élèves apprennent à dénombrer, elles et ils associent machinalement chaque nombre 1, 2, 3, 4, 5 à l’un des objets dans un ensemble d’objets donnés sans nécessairement saisir que 5, le résultat du dénombrement, correspond aussi à la quantité d’objets dans l’ensemble. Le lien entre la quantité et le nombre qui la représente est fort complexe. Un même nombre, par exemple 2, peut décrire des réalités très différentes. Il peut représenter à la fois 2 pommes, 2 pains ou 1 pomme et 1 pain. Il peut représenter aussi bien 2 gros ballons que 2 petits ballons. Ainsi, même si les ensembles d’objets sont différents, la quantité d’objets dans chacun des ensembles est la même. La complexité est accrue lorsque la quantité fait référence à une mesure, comme la longueur, la masse et la capacité, puisque les « objets quantifiés », c’est-à-dire les unités de mesure (cm, kg ou ml, par exemple), ne sont pas manipulables comme le sont, par exemple, les pommes, les pains ou les ballons.
Il est important de saisir la notion de quantité pour comprendre le concept de valeur de position.
Le concept de quantité intervient dans la compréhension du concept de valeur de position des chiffres qui composent un nombre. Cette valeur augmente successivement d’un facteur 10 lorsqu’on lit les chiffres de droite à gauche et diminue d’un facteur 10 lorsqu’on les lit de gauche à droite. La compréhension du concept de valeur de position s’avère aussi très utile lorsque les élèves commencent à utiliser des nombres plus grands ou des nombres décimaux.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 44.
Développer une compréhension conceptuelle du dénombrement a un lien direct avec la compréhension de la quantité et la valeur de position.
En dénombrant dans le cadre d’activités concrètes, les élèves acquièrent les concepts et les stratégies de base qui les aident à comprendre la valeur quantitative du nombre. Elles et ils apprennent à compter avec précision, à reconnaître les régularités dans le système de numération en base 10 (11, 12, 13…; 21, 22, 23…; 31, 32, 33…) et à faire des liens entre ces régularités et la valeur de position des chiffres qui composent les nombres. Le personnel enseignant doit tenir compte du fait que certains nombres sont particulièrement difficiles à apprendre en français. Il suffit de penser, par exemple, à un nombre comme 12, que des élèves appelleront spontanément « dix-deux ».
Exemple 1
Aider les élèves à apprendre le nom des nombres de 11 à 16 et à reconnaître qu’ils ne suivent pas la régularité des nombres de 20 à 49 (vingt et un, trente et un, quarante et un, par exemple). Leur faire remarquer que les nombres de 11 à 16 sont formés à partir des nombres de 1 à 6 et que certains commencent par les mêmes lettres (deux et douze; trois et treize; quatre et quatorze; six et seize).
Exemple 2
Aider les élèves à repérer, dans une grille de nombres, des régularités telles que :
- Le chiffre 9 termine toujours la dizaine (29, 39, 49, par exemple).
- Dans la suite 10, 20, 30…, le chiffre des dizaines suit la même séquence que 1, 2, 3…
- La suite de nombres à l’intérieur de chaque dizaine est formée à partir de 1, de 2, de 3… (20 se combine à 1 pour devenir 21, puis à 2 pour devenir 22, et ainsi de suite).
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 12.
Éléments sous-jacents
Selon les écrits les plus récents en éducation, les éléments ci-dessous sont considérés comme des fondements au développement du concept de quantité.
Conservation du nombre
Les travaux de Piaget (1965) portant sur de jeunes enfants ont révélé que ces dernières et derniers avaient une fausse conception de la quantité. Au cours d’une expérience, des jetons disposés sur une table ont été éloignés les uns des autres, et les enfants devaient dire si la quantité était demeurée la même ou si elle était différente. Elles et ils ont répondu qu’il y avait maintenant plus de jetons, manifestant ainsi leur incompréhension du concept de conservation du nombre, à savoir que la quantité demeure constante, même si l’on disperse les éléments pour donner l’impression d’un plus grand nombre. Par ailleurs, les élèves qui ont saisi ce concept comprennent que l’on ne peut modifier une quantité d’objets qu’en y ajoutant ou en y retranchant des éléments.
Poser aux élèves la question suivante : Quelle rangée contient le plus d’objets?
Reconnaissance globale d’une quantité
L’habileté à reconnaître globalement une quantité est l’habileté à quantifier les éléments d’un ensemble d’objets donné sans dénombrer chacun des éléments. Les activités conçues pour développer cette habileté (à l’aide de cartes à pois, par exemple) aident les élèves à acquérir une représentation mentale de la quantité associée à un nombre.
Cartes à pois :
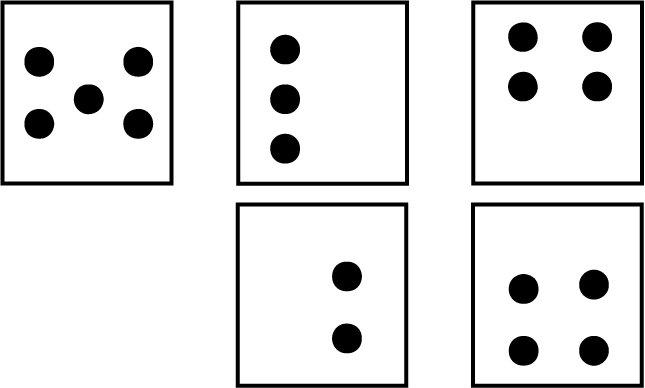image L’image présente deux rangées de cartes à pois : la première rangée contient trois cartes, tandis que la deuxième en contient deux. La première carte contient cinq pois, la deuxième en contient trois, la troisième en contient quatre, la quatrième en contient deux, et la cinquième en contient quatre.
Points d’ancrage 5 et 10
Les élèves saisissent davantage le sens de la quantité en envisageant certains nombres par rapport à un point d’ancrage comme le nombre 5 ou le nombre 10; par exemple, 2, c’est 3 de moins que 5 dans un cadre à cinq cases. Le fait de se rappeler les regroupements qui donnent 10, comme 6 + 4 ou 7 + 3, ou le fait de reconnaître que certains nombres peuvent représenter un regroupement de 10 et d’un autre nombre, comme 12, qui est le résultat de 10 + 2, est utile pour approfondir le sens du nombre.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 45-47.
Connaître les points d’ancrage 5 et 10 et leurs liens avec les autres nombres facilite la compréhension de la valeur de position. Les élèves prennent conscience des relations entre les nombres dès qu’elles et ils commencent à compter sur leurs doigts. C’est alors que les élèves découvrent les relations qui existent entre les nombres de 1 à 4 et le nombre 5, et les nombres de 1 à 9 et le nombre 10. La compréhension de ces relations les aide à reconnaître, par exemple, que dans un cadre à 10 cases, où l’on a posé des jetons sur toutes les cases sauf sur une, on a représenté le nombre 9. Cette compréhension est par la suite élargie, d’abord aux relations entre les nombres de 0 à 10 et les points d’ancrage 5 et 10, puis aux nombres plus grands.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 63.
Habileté : représenter les nombres naturels
L’habileté à représenter un nombre implique de savoir le lire et l’écrire en lettres et en chiffres, et de passer aisément d’une représentation à l’autre.
Dès les premières années d’études, un des aspects importants de la représentation des nombres consiste à apprendre comment les lire, les nommer et les écrire, puis à faire le lien entre leur graphie en lettres et leur graphie en chiffres, et à comprendre ce qu’ils représentent.
Les jeunes enfants doivent apprendre à maîtriser l’écriture des chiffres de 0 à 9. Pour ce faire, Baroody (1997) suggère d’aider les enfants à reconnaître les caractéristiques de chacun des chiffres; par exemple, le 1 ressemble à un bâton; le 9 ressemble à un ballon au bout d’un bâton. Il importe aussi que les élèves s’exercent à écrire les chiffres à partir de contextes intéressants et motivants, par exemple, en simulant l’achat d’aliments à l’épicerie, plutôt que dans un contexte de pratique répétitive. Cette habileté implique aussi d’être capable d’utiliser différents moyens visuels (cadre à dix cases ou autre matériel de manipulation) et différents médiums (matériel tactile, gouache, collage, craie, grille) pour représenter le nombre.
L’habileté à saisir les liens qui existent entre la représentation symbolique des nombres et la quantité qu’ils évoquent est essentielle à l’acquisition du sens du nombre.
Au cours des premières années d’études, plusieurs élèves ont de la difficulté à comprendre que la quantité représentée par un chiffre dépend de sa position dans un nombre.
Exemple
L’expérience ci-après en témoigne. On a demandé à des élèves de dénombrer 26 cubes. Lorsqu’on leur a demandé d’écrire le nombre de cubes, les élèves ont su écrire 26. Lorsqu’on leur a demandé de montrer les cubes qui représentaient le chiffre des unités (6), les élèves ont su le faire. Cependant, lorsqu’on leur a demandé de montrer les cubes qui représentaient le chiffre des dizaines (2), les élèves ont montré 2 cubes, sans être capables d’expliquer la raison pour laquelle il restait encore autant de cubes.
Il importe donc de proposer aux élèves de nombreuses activités consistant à décomposer des nombres en dizaines et en unités afin de les aider à saisir le concept de la quantité liée à la valeur de position.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 72-73.
Dans la vidéo suivante, les élèves construisent différentes représentations d’un nombre à l’aide du matériel de base 10 (Digi-Blocks).
Description de la vidéo
Description à venir
Habileté : décrire les façons dont les nombres sont utilisés dans la vie quotidienne
Pour comprendre le concept d’un nombre, il faut établir des liens entre le symbole, par exemple, 4, le mot, c’est-à-dire quatre, la quantité, par exemple, 4 objets, ou le rang, c’est-à-dire le quatrième pupitre dans une rangée. Les nombres sont aussi parfois utilisés comme simple code, sans référence à une quantité ou à un rang; par exemple, 4 dans un numéro de téléphone ou sur un maillot de soccer. Les adultes, qui ont, depuis longtemps, compris que le sens des nombres dépend du contexte dans lequel ils sont utilisés, n’ont souvent pas conscience de la difficulté que peuvent avoir les élèves à saisir ces différences.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 73.
Connaissance : nombres naturels
Les nombres naturels appartiennent à l’ensemble N = {0, 1, 2, 3, 4, 5, 6, 7, 8…}.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.