B1.7 Reconnaître l’équivalence entre un demi et deux quarts d’un même tout, dans des contextes de partage équitable d’une quantité.
Habileté : reconnaître l’équivalence
Reconnaître l’égalité de deux fractions, c’est reconnaître que les deux fractions représentent la même quantité.
La notion de fractions équivalentes est abordée pour la première fois en 1re année. Il est parfois difficile pour les élèves de saisir qu’une quantité peut porter plusieurs noms et être représentée par plusieurs nombres; par exemple, le nombre \(\frac{1}{2}\) représente la même quantité que le nombre \(\frac{2}{4}\); donc, on peut affirmer que \(\frac{1}{2}\ = \frac{2}{4}\).
La compréhension des fractions équivalentes fait partie du raisonnement proportionnel que les élèves vont continuer à développer au cours des prochaines années.
Déterminer des fractions équivalentes, c’est déterminer des fractions qui représentent la même quantité. On cherche alors un nombre de « petites parties » d’un tout qui correspondent à un nombre particulier de « grandes parties » du même tout; par exemple, si l’on cherche le nombre de quarts qui correspond à une demie, on peut représenter les deux fractions à l’aide de modèles de surface identiques afin de reconnaître l’équivalence :
 image
Deux rectangles sont placés côte à côte. Le premier rectangle est divisé en deux parties égales sur le sens de la
largeur. Sa première moitié est violette tandis que l’autre est blanche. Le deuxième rectangle est identique, sauf
qu’il est également séparé dans le sens de la longueur.
image
Deux rectangles sont placés côte à côte. Le premier rectangle est divisé en deux parties égales sur le sens de la
largeur. Sa première moitié est violette tandis que l’autre est blanche. Le deuxième rectangle est identique, sauf
qu’il est également séparé dans le sens de la longueur.
La relation d’équivalence doit aussi être explorée relativement aux fractions d’un ensemble. Dans l’image ci-dessous, les élèves voient aisément que \(\frac{2}{4}\) des bonbons sont emballés dans des papillotes mauves. Toutefois, elles et ils peuvent avoir de la difficulté à déterminer la fraction équivalente de \(\frac{1}{2}\). Il importe alors de présenter des activités où elles et ils pourront manipuler les éléments de l’ensemble. Ainsi, les élèves peuvent les grouper en ensembles de deux et déterminer la fraction équivalente.

\(\frac{2}{4}\) des bonbons sont emballés dans des papillotes mauves.
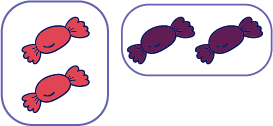
\(\frac{1}{2}\) des bonbons sont emballés dans des papillotes mauves.
Source : adapté de Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 50-52.
Connaissance : fraction
La compréhension de la représentation de quantités par des fractions aide à approfondir le concept de quantité. Il importe de comprendre que les fractions, comme un demi, un tiers ou un quart, représentent des quantités différentes selon qu’elles font référence à une partie d’un tout (une longueur, une surface ou un solide) ou à une partie d’un ensemble; par exemple, un tiers d’une tablette de chocolat (partie d’un tout) représente une quantité de chocolat en fonction de la grosseur de la tablette originale. Cependant, un tiers d’une douzaine d’œufs (partie d’un ensemble) représente quatre œufs.
image Deux morceaux de palette de chocolat et une douzaine d’œufs sont placés côte à côte. Au-dessus du premier morceau de chocolat à gauche, qui contient trois carrés, il est écrit : « Parties d’un tout ». Une flèche au troisième carré mentionne la fraction un tiers. Au centre, il y a un morceau de chocolat à trois carrés. Le carré du bas possède une flèche qui mentionne la fraction un tiers. Et à droite, il y a une douzaine d’œufs dont les quatre derniers œufs à droite sont encerclés. Une flèche part de l’ensemble de quatre et mentionne la fraction un tiers. Et au-dessus des œufs, il est écrit : « Partie d’un ensemble ».
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 48.
Donner aux élèves des occasions de découvrir :
- que, lorsque la fraction représente une région (modèle de surface), l’aire de chaque partie doit être de mesure équivalente;
- que, lorsque les fractions sont utilisées pour décrire des ensembles (modèle d’ensemble), les objets composant les ensembles peuvent être de tailles différentes (si l’on dit que \(\frac{1}{2}\) du bol de fruits est composée de pommes, l’autre \(\frac{1}{2}\) peut être composée de raisins qui ont une taille inférieure à celle des pommes, par exemple);
- que la fraction représente une partie d’un tout.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 30.
Connaissance : un demi
Lorsqu’un tout est divisé en deux parties équivalentes, chaque partie est la moitié de la quantité originale. Deux demis donnent un tout.
Note : En 1re année, les élèves devraient apprendre la terminologie liée aux termes moitié et demi. La moitié d’une moitié est un quart.
Source : En avant, les maths! CM, Nombres, p. 2.
Connaissance : un quart
Lorsqu’un tout est partagé en quatre parties équivalentes, chaque partie est le quart de la quantité originale. Quatre quarts donnent un tout.
Note : L’utilisation de fractions unitaires améliore la compréhension de la quantité. Lorsque les élèves comptent en nommant les fractions unitaires, cela les aide à voir les parties de la fraction au cours de la composition et de la décomposition de fractions. Alors, il faut lire les fractions ainsi : un quart, 2 un quart, 3 un quart, 4 un quart*.
* Fractions Learning Pathways, Unit D – Use unit fractions to name and count fractional amounts.
Source : En avant, les maths! CM, Nombres, p. 2.
Connaisance : fractions équivalentes
Deux fractions sont équivalentes si elles représentent la même quantité.
Note : En 1re année, il est important de souligner qu’il s’agit de fractions d’un même tout. Une même partie d’un tout peut être représentée par différentes fractions; par exemple, un demi et deux quarts [2 un quart] sont des fractions équivalentes.
Note : Les problèmes de partage entre quatre personnes donnent l’occasion de montrer qu’un demi et 2 quarts sont équivalents.
Source : En avant, les maths! CM, Nombres, p. 3.
