B2.1 Utiliser les propriétés de l’addition et de la soustraction ainsi que la relation entre l’addition et la soustraction pour résoudre des problèmes et vérifier la vraisemblance des calculs.
Habileté : utiliser les propriétés de l’addition et de la soustraction pour résoudre des problèmes et vérifier la vraisemblance des calculs
« L’utilisation des propriétés des opérations et des relations entre les opérations nous permet de construire des phrases numériques et de les manipuler avec souplesse de manière à résoudre des équations et à simplifier des calculs. » [traduction libre]
(Department of Education and Training of Western Australia)
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, 97.
Il n’est pas nécessaire que les élèves du primaire connaissent le nom des propriétés. Il suffit qu’elles et ils les utilisent naturellement pour combiner des nombres.
Les élèves montrent leur compréhension des propriétés des opérations mathématiques avec des objets ou des nombres précis. Les élèves utilisent du matériel concret, des dessins, des mots ou des symboles pour représenter des idées mathématiques et des relations.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 17.
Les propriétés de l’addition sont :
- la commutativité (par exemple, \(\ 1 + 2 = 2 + 1\));
- le nombre zéro (0) en tant qu’élément neutre (par exemple, \(\ 1 + 0 = 1\) et \(\ 0 + 1 = 1\)).
La propriété de la soustraction est :
- le nombre zéro (0) en tant qu’élément neutre (par exemple, \(\ 1 - 0 = 1\)).
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 33.
La commutativité
Les élèves qui reconnaissent la propriété de commutativité de l’addition peuvent réduire de moitié la quantité de faits numériques qu’il leur faut apprendre. La représentation visuelle de faits comme \(\ 3 + 2\) et \(\ 2 + 3\) aide les élèves à saisir cette relation.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 19.
image Une ligne de dénombrement pointe à gauche comme à droite. Elle est divisée en six parts. En haut, il y a une réglette rouge qui mesure deux parts, et une réglette jaune qui mesure trois parts. Il est écrit l’équation deux plus trois. En bas, il y a une réglette jaune qui mesure trois parts et une réglette rouge qui mesure deux parts. Il est écrit l’équation trois plus deux.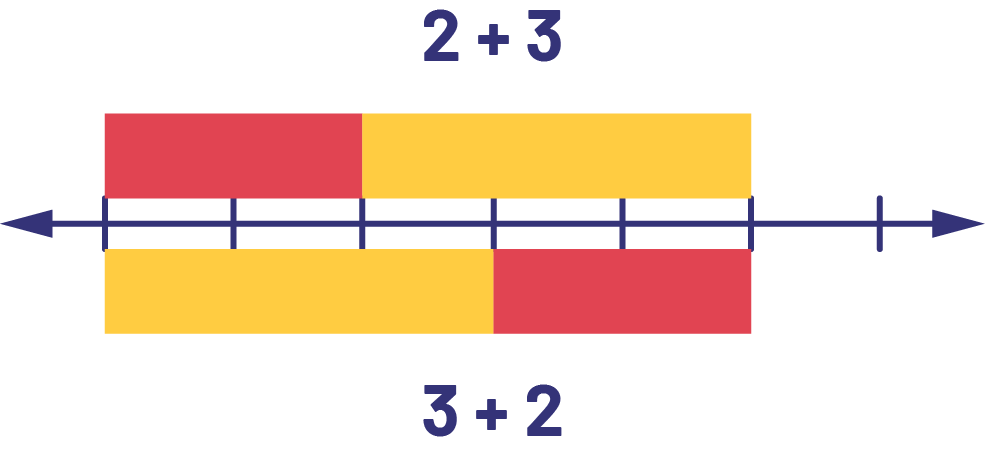
Élément neutre (propriété du nombre 0 dans l’addition et la soustraction)
En ayant recours à la propriété du nombre 0 dans l’addition, le personnel enseignant incite les élèves à proposer des conjectures telles que : « Si j’ajoute 0 à une quantité (par exemple, \(\ 5 + 0\)), cette quantité reste pareille et si j’ajoute une quantité quelconque à 0 (par exemple, \(\ 0 + 5\)), j’obtiens la quantité ajoutée. »
En appliquant ces conjectures à différents nombres, les élèves seront en mesure de formuler une généralisation, à savoir que cette propriété du nombre 0 est vraie pour tous les nombres.
Pour le rôle du 0 dans la soustraction, le personnel enseignant incite les élèves à proposer une conjecture telle que : « Quand je soustrais 0 d’un nombre (par exemple, \(\ 5 - 0\)), j’obtiens le nombre de départ. » En appliquant cette conjecture à différents nombres, les élèves seront en mesure de formuler une généralisation, à savoir que cette propriété du nombre 0 est vraie pour tous les nombres.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 93 et 95.
Habileté : utiliser la relation entre l’addition et la soustraction pour résoudre des problèmes et vérifier la vraisemblance des calculs
Relations entre l’addition et la soustraction
La compréhension des liens entre les opérations (par exemple, l’addition et la soustraction sont des opérations inverses) aide les élèves à apprendre les faits numériques de base et à résoudre des problèmes.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 32.
L’addition et la soustraction sont des opérations inverses. Or, lorsqu’elles et ils sont en apprentissage, les élèves ont souvent de la difficulté à résoudre des équations telles que \(\ 17 + \mathord{?} = 31\). Le personnel enseignant incite alors leurs élèves à utiliser l’opération inverse, soit la soustraction. Or, il peut s’agir d’apprendre un truc, à moins que les élèves comprennent la raison pour laquelle la soustraction est une stratégie possible.
Les élèves doivent d’abord saisir la relation du tout et de ses parties, ainsi que le sens d’une différence. Par exemple, un nombre peut être représenté comme suit :
image Deux rectangles sont placés l’un sous l’autre. Dans le premier, il est écrit le nombre 18. Dans le deuxième, le rectangle est divisé en deux parties égales. Dans la première partie, il est écrit le nombre dix, et dans la deuxième partie, le chiffre huit.
Cette façon de représenter la relation entre un nombre et ses parties permet de voir que la soustraction est l’opération inverse de l’addition. Ainsi, puisque \(\ 10 + 8 = 18\) et \(\ 8 + 10 = 18\), donc \(\ 18 − 10 = 8\) et \(\ 18 \ – \ 8 = 10\). De plus, les élèves peuvent constater que l’addition est commutative (\(\ 10 + 8 = 8 + 10\)) et que la soustraction ne l’est pas (\(\ 18 – 10 ≠ 10 – 18\)). Celles et ceux qui ont acquis un bon sens du nombre et qui sont capables de décomposer et de regrouper des nombres peuvent mettre leurs connaissances à profit pour résoudre plus efficacement des équations telles que \(\ 10 + \mathord{?} = 18\) en comprenant que l’on cherche la différence entre 10 et 18.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 97-98.
Connaissance : propriétés des opérations
Les propriétés des opérations sont des caractéristiques qui sont propres aux opérations, peu importe les nombres en cause; à titre d’exemple, l’addition est commutative puisque \(\ 3 + 5 = 5 + 3 = 8\), \(\ 4 + 7 = 7 + 4 = 11\).
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, 102.
Connaissance : commutativité
La commutativité s’explique par le fait que le résultat d’une opération ne change pas lorsqu’on intervertit l’ordre des termes qui la composent. L’addition est commutative. La soustraction n’est pas une opération commutative puisque le résultat de la première est supérieur à zéro, et celui de la deuxième est inférieur à zéro.
Exemple
\(\ 2 + 3 = 3 + 2\)
\(\ 6 - 3 ≠ 3 - 6 \)
Source : adapté de Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, 102.
Connaissance : élément neutre (rôle du nombre 0 dans l’addition et la soustraction)
Comme son nom l’indique, un élément neutre est un nombre qui n’a aucun effet pour une opération donnée. Ainsi, le nombre 0 est l’élément neutre de l’addition (par exemple, \(7 + 0 = 7\) et \(0 + 7 = 7\)).
Dans une soustraction, le nombre 0 ne produit aucun effet seulement lorsqu’il est le deuxième terme (par exemple, \(3 \ – \ 0 = 3\)).
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 107.
