B2.4 utiliser des objets, des schémas et des équations pour représenter, décrire et résoudre des situations relatives à l’addition de nombres naturels dont la somme est égale ou inférieure à 50 et à la soustraction de nombres égaux ou inférieurs à 50.
Habileté : représenter, décrire et résoudre des situations
En plus d’enseigner les opérations arithmétiques à partir de stratégies et du raisonnement s’y rattachant, il est important de présenter ces opérations dans des contextes de résolution de problèmes. Lors de la résolution de problèmes, on encourage les élèves à utiliser les connaissances déjà acquises et à établir des liens avec le nouvel apprentissage. Ces liens peuvent être rompus si on ne présente pas aux élèves un éventail diversifié de problèmes. Les élèves qui n’apprennent pas à calculer dans des contextes de résolution de problèmes pourraient avoir beaucoup de difficulté à établir ces liens plus tard. Leur compréhension de la notion abstraite du nombre et de son application risque d’être floue, et il est possible que quelques élèves n’arrivent pas à utiliser efficacement des stratégies de calcul pour résoudre des problèmes.
Le recours à des contextes de résolution de problèmes est tout aussi important pour les opérations sur les nombres à plusieurs chiffres. Lorsqu’on donne des problèmes aux élèves, lorsqu’on les encourage à trouver un algorithme et à l’utiliser de manière souple, on leur donne l’occasion d’approfondir leur compréhension des opérations. Par souci d’efficacité et croyant bien faire, on enseigne souvent aux élèves l’algorithme à utiliser pour effectuer les opérations sur les nombres à plusieurs chiffres. Cette méthode leur étant présentée comme la « bonne façon » de résoudre le problème, les élèves font des efforts ardus pour comprendre et mémoriser cette procédure. Cette méthode entraîne souvent une utilisation peu efficace de l’algorithme, un manque d’exactitude et une compréhension limitée. Si, au contraire, on encourage les élèves à dégager le sens du problème et à élaborer leurs propres stratégies pour le résoudre, elles et ils montreront plus d’aisance et plus de précision dans leur travail sur les opérations.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 5.
À cet égard, le recours à des problèmes écrits, c’est-à-dire des problèmes présentés sous forme d’énoncés, constitue l’une des stratégies les plus efficaces pour comprendre les opérations et ainsi aider les élèves à cheminer dans la compréhension de problèmes.
Problèmes écrits relatifs à l’addition et à la soustraction
Les élèves acquièrent une bonne compréhension de l’addition et de la soustraction ainsi que des relations entre les nombres en résolvant des problèmes écrits. Devant un problème comme celui-ci : Pascale a quelques billes; quelqu’un lui en donne 3 de plus et elle en a maintenant 8. Combien Pascale en avait-elle au départ? Notons que si l’adulte ne voit pas de difficulté à résoudre ce genre de problème, il en est tout autrement pour l’enfant. En recourant à la modélisation pour représenter le problème, puis en lui rattachant une opération, le personnel enseignant aide les élèves à faire des rapprochements entre la compréhension conceptuelle et la maîtrise des procédures dans le cadre de problèmes ayant différents degrés de complexité.
Les types de problèmes ci-dessous présentés à l’aide d’exemples peuvent aider les élèves à percevoir les faits numériques de base relatifs à l’addition et à la soustraction de diverses façons : par l’ajout, le retrait, la réunion et la comparaison. Le recours aux problèmes pour présenter les faits numériques de base oblige les élèves à raisonner pour trouver des solutions et permet ainsi de développer un meilleur sens des opérations.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 8.
Les problèmes d’ajout et de retrait sont perçus par les élèves comme des situations actives, plus faciles à modéliser et à « voir », car la quantité initiale augmente ou diminue. Les problèmes de réunion, cependant, supposent une situation statique, car aucune action ou aucun changement ne se produit, ce qui les rend plus abstraits et plus difficiles à comprendre. Les problèmes de comparaison, quant à eux, traitent de la relation entre deux quantités en les opposant : il n’y a donc pas d’action, mais une comparaison d’une quantité à une autre.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 83.
Problèmes d’ajout
Le modèle partie-tout peut être utile pour représenter les valeurs connues et inconnues dans des problèmes d’ajout. Le modèle d’ensemble est utile pour représenter l’ajout d’une quantité.
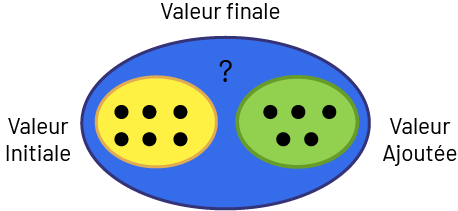
- Ajout : Valeur finale inconnue. Jamil a 6 bonbons. Il en achète 5 de plus. Combien de bonbons Jamil a-t-il à présent?
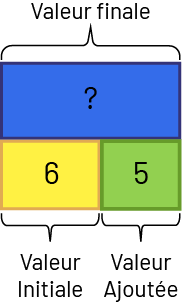image Un rectangle est divisé en trois parties. Au-dessus, il y a l’expression « Valeur Finale »
vers laquelle pointe une accolade qui englobe la première partie du rectangle. La première partie du rectangle,
au-dessus, s’étend sur toute la longueur est prend un peu plus de largeur que les deux autres parties en dessous.
Elle est bleue et marquée d’un point d’interrogation. En dessous, il y a une partie jaune, marquée du chiffre six,
légèrement plus volumineuse que la troisième partie, qui est verte et marquée du chiffre cinq.Sous la partie
jaune, il y a une accolade qui l’englobe et sous laquelle il est écrit « Valeur Initiale ». Sous la partie verte,
il y a une accolade qui l’englobe et sous laquelle il est écrit « Valeur Ajoutée ». Sous ces expressions, il est
écrit l’équation suivante : « six plus cinq égale point d’interrogation ».
\(\ 6 + 5 = \mathord{?}\)
\(\ 6 + 5 = \mathord{?}\)
- Ajout : Valeur initiale inconnue. Jamil a quelques bonbons. Il en achète 5 de plus. Il en a 11 à présent. Combien de bonbons Jamil avait-il au début?
image Un rectangle est divisé en trois parties. Au-dessus, il y a l’expression « Valeur Finale »
vers laquelle pointe une accolade qui englobe la première partie du rectangle. La première partie du rectangle,
au-dessus, s’étend sur toute la longueur est prend un peu plus de largeur que les deux autres parties en dessous.
Elle est bleue et marquée du nombre onze. En dessous, il y a une partie jaune, marquée d’un point d’interrogation,
légèrement plus volumineuse que la troisième partie, qui est verte et marquée du chiffre cinq.Sous la partie jaune,
il y a une accolade qui l’englobe et sous laquelle il est écrit « Valeur Initiale ». Sous la partie verte, il y a
une accolade qui l’englobe et sous laquelle il est écrit « Valeur Ajoutée ». Sous ces expressions, il est écrit
l’équation suivante : « Point d'interrogation plus cinq égale onze ».
\(\mathord{?} + 5 = 11\)
- Ajout : Valeur ajoutée inconnue. Jamil a 6 bonbons. Il en achète quelques-uns de plus. Il en a 11 à présent. Combien de bonbons Jamil a-t-il achetés?
\(\ 6 + \mathord{?} = 11\)
Problèmes de retrait
Le modèle partie-tout peut être utile pour représenter les valeurs connues et inconnues dans des problèmes de retrait. Le modèle d’ensemble est utile pour représenter le retrait d’une quantité.
- Retrait : Valeur finale inconnue. Nadia a 15 $. Elle donne 5 $ à son frère. Combien lui reste-t-il de dollars à présent?
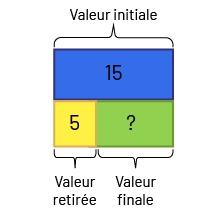image Un rectangle est divisé en trois parties. Au-dessus, il y a l’expression « Valeur Initiale »
vers laquelle pointe une accolade qui englobe la première partie du rectangle. La première partie du rectangle,
au-dessus, s’étend sur toute la longueur est prend un peu plus de largeur que les deux autres parties en dessous.
Elle est bleue et marquée du chiffre quinze. En dessous, il y a une partie jaune, marquée du chiffre cinq, moins
volumineuse que la troisième partie, qui est verte et marquée d'un point d’interrogation.Sous la partie jaune, il
y a une accolade qui l’englobe et sous laquelle il est écrit « Valeur retirée ». Sous la partie verte, il y a une
accolade qui l’englobe et sous laquelle il est écrit « Valeur finale ». Sous ces expressions sont écrites les
équations suivantes : « quinze moins cinq égale point d’interrogation » et « quinze moins cinq égale dix ».
\(\displaylines{\begin{align}15 \ - 5 &= \mathord{?} \\ 15 \ - 5 &= 10\end{align}}\)
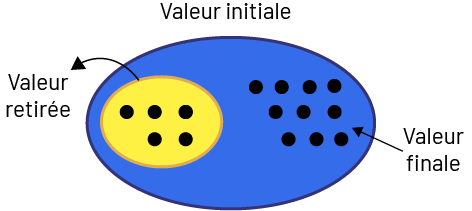image À côté du rectangle, il y a un ovale bleu. À gauche, il est écrit « Valeur retirée ». En
haut, il est écrit « Valeur initiale ». À droite, il est écrit « Valeur finale ». En bas, il est écrit « quinze
moins cinq égale point d’interrogation » et « quinze moins cinq égale dix ». Dans l’ovale bleu, il y a un ovale
jaune contenant cinq jetons noirs qui correspondent à la valeur retirée. Il y a aussi dix jetons noirs hors de
l’ovale jaune qui correspondent à la valeur finale.
\(\displaylines{\begin{align}15 \ - 5 &= \mathord{?} \\ 15 \ - 5 &= 10\end{align}}\)
- Retrait : Valeur retirée inconnue. Nadia a 15 $. Elle donne quelques dollars à son frère. Il lui reste 10 $ à présent. Combien de dollars Nadia a-t-elle donnés à son frère?
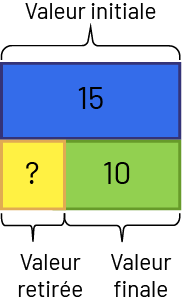
\(\displaylines{\begin{align}15 \ - \mathord{?} &= 10 \\ 15 \ - 10 &= 5 \mathord{, \ donc} \ 15 \ - 5 = 10\end{align}}\)
- Retrait : Valeur initiale inconnue. Nadia avait un certain nombre de dollars. Elle a donné 5 $ à son frère. Il lui reste 10 $ à présent. Combien Nadia avait-elle de dollars au début?
image Un rectangle est divisé en trois parties. Au-dessus, il y a
l’expression « Valeur Initiale » vers laquelle pointe une accolade qui englobe la première partie du rectangle. La
première partie du rectangle, au-dessus, s’étend sur toute la longueur est prend un peu plus de largeur que les deux
autres parties en dessous. Elle est bleue et marquée d'un point d’interrogation. En dessous, il y a une partie
jaune, marquée du chiffre cinq, moins volumineuse que la troisième partie, qui est verte et marquée du nombre
dix.Sous la partie jaune, il y a une accolade qui l’englobe et sous laquelle il est écrit « Valeur retirée ». Sous
la partie verte, il y a une accolade qui l’englobe et sous laquelle il est écrit « Valeur finale ». Sous ces
expressions il est écrit : « point d’interrogation moins cinq égale dix » et « dix plus cinq égale quinze, donc
quinze moins cinq égale dix ».
\(\displaylines{\begin{align}\mathord{?} \ - 5 &= 10 \\ 10 \ + 5 &= 15 \mathord{, \ donc} \ 15 \ - 5 = 10\end{align}}\)
Problèmes de réunion
Le modèle partie-tout peut être utile pour représenter les parties du tout connues et inconnues ou le tout connu ou inconnu dans des problèmes de réunion.
- Réunion : Partie du tout inconnue. Sonia a 8 crayons de couleur. Trois de ces crayons sont rouges. Les crayons qui restent sont bleus. Combien Sonia a-t-elle de crayons bleus?
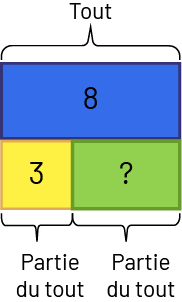image Un rectangle est divisé en trois parties. Au-dessus, il est écrit le mot « Tout », vers lequel
pointe une accolade qui englobe la première partie du rectangle. La première partie du rectangle, au-dessus, s’étend
sur toute la longueur est prend un peu plus de largeur que les deux autres parties en dessous. Elle est bleue et
marquée du chiffre huit. En dessous, il y a une partie jaune, marquée du chiffre trois, moins volumineuse que la
troisième partie, qui est verte et marquée d’un point d’interrogation.Sous la partie jaune, il y a une accolade qui
l’englobe et sous laquelle il est écrit « Partie du tout ». Sous la partie verte, il y a une accolade qui l’englobe
et sous laquelle il est écrit « Partie d’un tout ». Sous ces expressions il est écrit : « huit moins trois égale
point d’interrogation » et « huit moins trois égale cinq ».
\(\displaylines{\begin{align}8 \ - 3 &= \mathord{?} \\ 8 \ - 3 &= 5\end{align}}\)
- Réunion : Tout inconnu. Sonia a 3 crayons rouges et 5 crayons bleus. Combien Sonia a-t-elle de crayons de couleur?
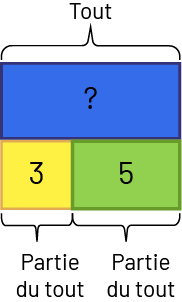
\(\displaylines{\begin{align}\mathord{?} \ - 3 &= 5 \\ 5 + 3 &= 8 \mathord{, \ donc\ }8 \ - 3 = 5\end{align}}\)
Problèmes de comparaison
Le modèle linéaire peut être utile pour représenter la différence entre deux nombres dans des problèmes de comparaison. Dans cet exemple, on utilise les réglettes Cuisenaire et la droite numérique double.
- Comparaison : Différence inconnue. Judith a 6 $ et Jeanne a 3 $. Combien de dollars Judith a-t-elle de plus que Jeanne? OU Judith a 6 $ et Jeanne a 3 $. Combien de dollars Jeanne a-t-elle de moins que Judith?
Je sais que la réglette vert foncé représente 6, alors je la place en haut de la droite numérique en partant du 0. Je sais que la réglette vert lime représente 3, alors je la place sous la droite numérique en partant du 0. Je compare les deux réglettes et je vois que la réglette vert lime est 3 de moins que la réglette vert foncé. Je trouve la différence ou l’écart entre les deux quantités. Il y a une différence de 3 $. Jeanne a 3 $ de moins que Judith.
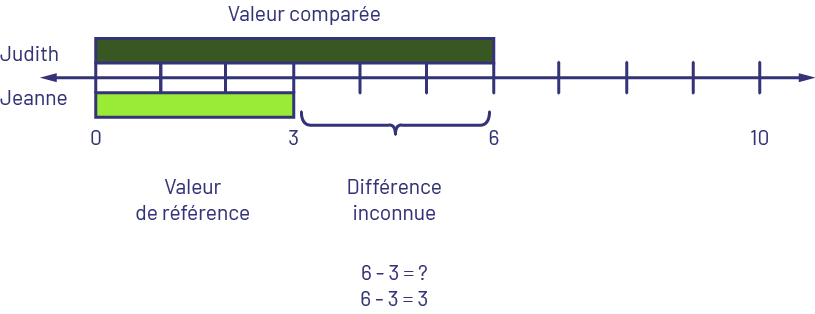image Une ligne de dénombrement est graduée de zéro à dix. Le haut de la droite correspond à Judith,
tandis que le bas correspond à Jeanne. En haut de la droite, il y a une barre vert foncé qui va de zéro à six.
Au-dessus de la barre vert foncé, il est écrit « Valeur comparée ». En bas de la droite, il y a une barre verte qui
va de zéro à trois. Une accolade va de trois à six. Sous la barre verte, il est écrit « Valeur de référence ». Sous
l’accolade, il est écrit « Différence inconnue. Six moins trois égale point d’interrogation. Six moins trois égale
trois ».
Comparaison : Valeur comparée inconnue. Judith a 3 $ de plus que Jeanne. Jeanne a 3 $. Combien de dollars Judith a-t-elle? OU Jeanne a 3 $ de moins que Judith. Jeanne a 3 $. Combien de dollars Judith a-t-elle?
Je sais que la réglette vert lime représente 3, alors je la place en haut de la droite numérique en partant du 0. Je prends une autre réglette vert lime et je la place sous la droite numérique en partant du 0 et j’ajoute une autre réglette vert lime puisque Judith a 3 $ de plus que Jeanne. Je remplace les deux réglettes vert lime par la réglette vert foncé qui représente 6. Judith a donc 6 $.
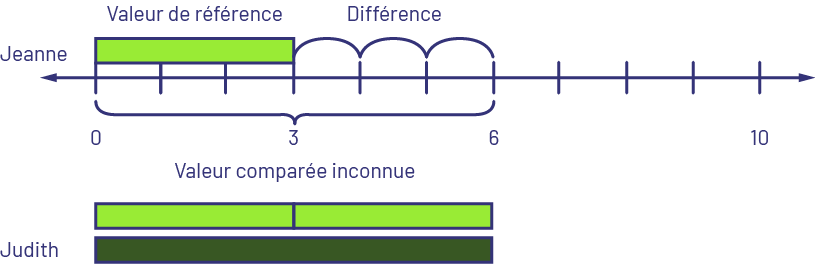image Une ligne de dénombrement est graduée de zéro à dix. À gauche du point zéro, au-dessus de la
flèche qui pointe à gauche, est écrit le nom de Jeanne. Au-dessus de la droite, une barre verte va de zéro à trois.
Au-dessus de la barre, il est écrit « Valeur de référence ». Des traits courbes faisant le bond de trois à quatre, de
quatre à cinq et de cinq à six représentent la différence. Sous la droite, une accolade va de zéro à six. Sous
celle-ci apparaît la mention « valeur comparée inconnue ». Sous cette mention, il y a une barre verte qui va de zéro à
six, divisée en deux au centre, vis-à-vis le trois. Et sous cette barre, il y a une barre vert foncé de la même
longueur. À gauche, l’on trouve le nom de Judith.
- Comparaison : Valeur de référence inconnue. Judith a 6 $ et Jeanne a 3 $ de moins que Judith. Combien de dollars Jeanne a-t-elle? OU Jeanne a 3 $ de moins que Judith. Judith a 6 $. Combien de dollars Jeanne a-t-elle?
Je sais que la réglette vert foncé représente 6, alors je la place en haut de la droite numérique en partant du 0. Sur la droite numérique, je compte à rebours de trois bonds pour arriver à 3 pour représenter que Jeanne a 3 $ de moins que Judith. Je prends une réglette vert lime et je la place sous la droite numérique en partant du 0. Jeanne a 3 $.
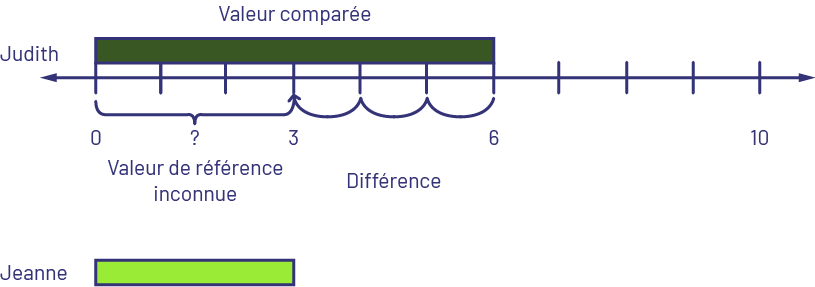image Une ligne de dénombrement est graduée de zéro à dix. À gauche du point zéro, au-dessus de la
flèche qui pointe à gauche, est écrit le nom de Judith. Au-dessus de la droite, une barre vert foncé va de zéro à six.
Au-dessus de la barre, il est écrit « Valeur comparée ». Sous la droite, une accolade va de zéro à trois, sous
laquelle il est écrit « Valeur de référence inconnue ». Des traits courbes faisant le bond de trois à quatre, de
quatre à cinq et de cinq à six représentent la différence. En dessous, il y a une barre verte qui va de zéro à trois.
À gauche de cette barre, on trouve le nom de Jeanne.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 8-10.
Connaissance : problème d’ajout
Dans les problèmes axés sur l’ajout, le résultat est le plus grand.
image Problème d’ajout. L’image montre un ovale brisé en deux sur le sens de la longueur et un ovale intact. À gauche, on trouve la partie inférieure de l’ovale, nommée Valeur initiale. En dessous, il est écrit : « Montant de départ, plus petit que le montant obtenu ». Une flèche pointe vers la moitié supérieure de l’ovale brisé, nommée Valeur ajoutée. En dessous, il est écrit : « Montant ajouté, plus petit que le montant obtenu ». Une flèche pointe vers l’ovale entier, nommé Valeur finale. En dessous, il est écrit : « Montant obtenu ».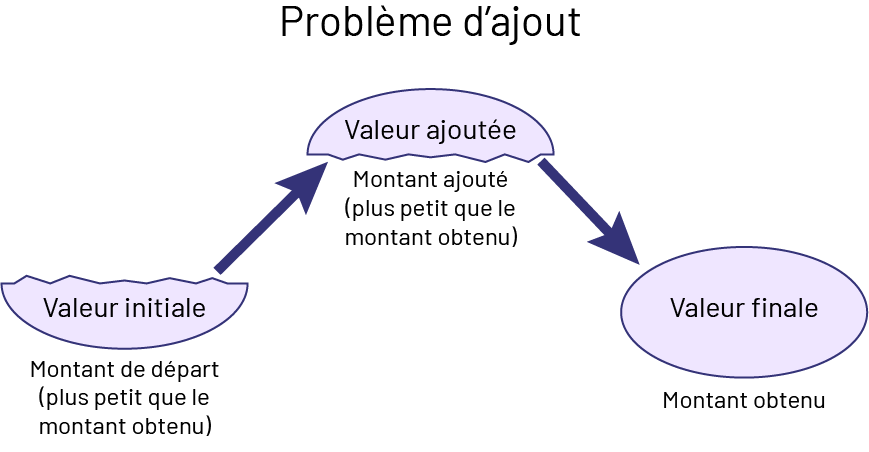
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 9.
Exemple
Camille a 5 billes. Luc lui en donne 8. Combien de billes a-t-elle en tout?
Valeur finale inconnue : \(\ 5 + 8 = \mathord{?}\)
Camille a 5 billes. Il lui faut 13 billes pour son jeu. Combien lui en manque-t-il?
Valeur ajoutée inconnue : \(\ 5 + \mathord{?} = 13\)
Camille a des billes. Luc lui en donne 5 de plus. Maintenant, elle en a 13. Combien de billes avait-elle au début?
Valeur initiale inconnue : \(\mathord{?} + 5 = 13\)
Source : L’@telier - Ressources pédagogiques en ligne (atelier.on.ca).
Connaissance : problème de retrait
Dans les problèmes de retrait, le premier montant est le plus grand.
image Problème de retrait. L’image montre un ovale brisé en deux sur le sens de la longueur et un ovale intact. À gauche, on trouve l’ovale intact, nommé Valeur initiale. En dessous, il est écrit : « Montant de départ, plus grand montant ». Une flèche pointe vers la moitié supérieure de l’ovale brisé, nommée Valeur retirée. En dessous, il est écrit : « Montant enlevé ». Une flèche pointe vers la partie inférieure de l’ovale, nommée Valeur finale. En dessous, il est écrit : « Montant obtenu ».
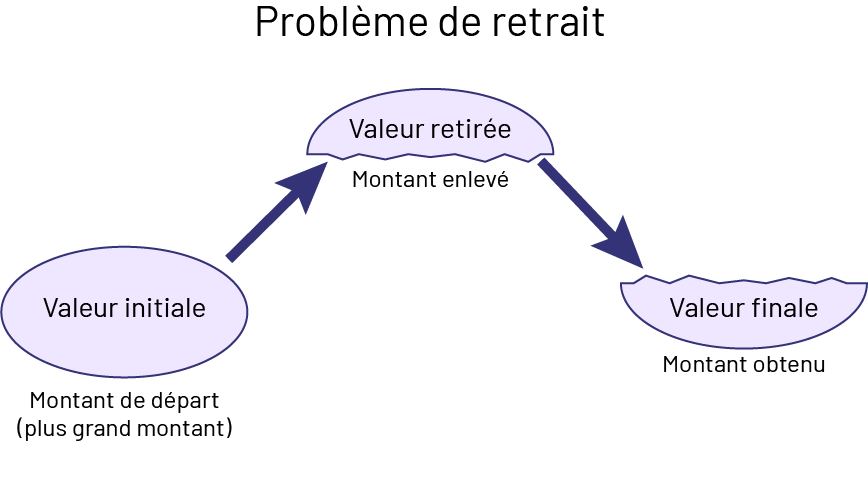
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 9.
Exemple
Camille a 13 billes. Elle en donne 5 à son ami Luc. Combien lui en reste-t-il?
Résultat inconnu : \(\ 13 \ – 5 = \mathord{?}\)
Camille a 13 billes. Elle en donne à son ami Luc. Maintenant, il lui en reste 8. Combien de billes a-t-elle données à Luc?
Valeur retirée inconnue : \(\ 13 \ – \mathord{?} = 8\)
Camille a des billes. Elle en donne 5 à son ami Luc. Maintenant, elle en a 8. Combien de billes avait-elle au début?
Valeur initiale inconnue : \(\mathord{?} \ – 5 = 8\)
Source : L’@telier - Ressources pédagogiques en ligne (atelier.on.ca).
Connaissance : problème de réunion
Les problèmes axés sur la relation partie-partie-tout comprennent deux parties qui sont réunies en un tout.
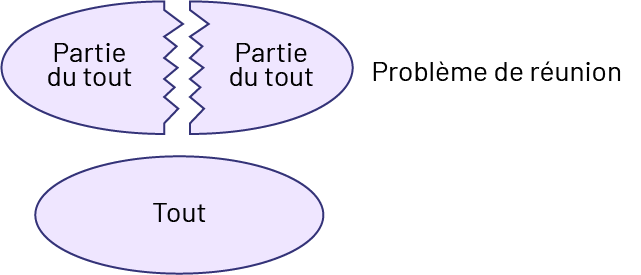image L’image présente deux ovales placés l’un sous l’autre. Le premier ovale est brisé en deux dans
le sens de la largeur, et il est écrit « Partie d’un tout » sur chacune des moitiés. Il est écrit « Problème de
réunion » à côté de l’ovale brisé. Le deuxième ovale, qui est intact, représente le tout.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 9.
Exemple
Camille a 5 billes rouges et 8 billes jaunes. Combien de billes a-t-elle?
Tout inconnu : \(\ 5 + 8 = \mathord{?}\)
Camille a 13 billes : 5 sont rouges et les autres sont jaunes. Combien de billes jaunes a-t-elle?
Partie d’un tout inconnue : \(\ 5 + \mathord{?} = 13\)
Source : L’@telier - Ressources pédagogiques en ligne (atelier.on.ca).
Connaissance : problème de comparaison
Dans les problèmes de comparaison, il s’agit de comparer deux quantités. La troisième quantité représente la différence.
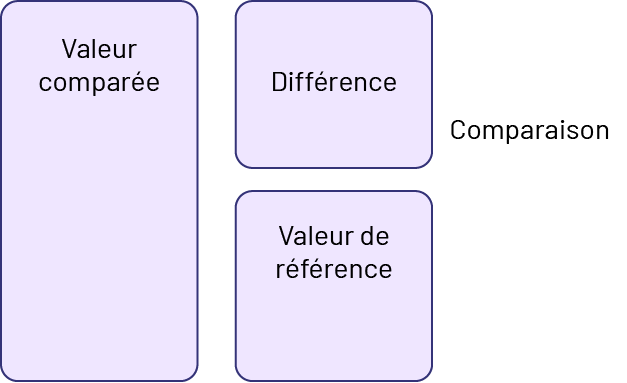image Un rectangle sur lequel il est écrit « Valeur comparée » avoisine deux carrés placés l’un sous
l’autre. Sur le carré du dessus, il est écrit « Différence », tandis que sur le carré du dessous, il est écrit «
Valeur de référence ». À côté du carré du dessus, il est écrit « Comparaison ».
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 10.
Exemple
Camille a 13 billes. Luc en a 8. Combien de billes Camille a-t-elle de plus que Luc?
Différence inconnue : \(\ 13 \ - 8 = \mathord{?}\)
Luc a 5 billes. Camille a 8 billes de plus que Luc. Combien Camille a-t-elle de billes?
Valeur comparée inconnue : \(\mathord{?} \ – 8 = 5\)
Camille a 13 billes. Elle en a 5 de plus que Luc. Combien Luc a-t-il de billes?
Valeur de référence inconnue : \(\ 13 - \mathord{?} = 5\)
Source : L’@telier - Ressources pédagogiques en ligne (atelier.on.ca).