B1.3 Estimer le nombre d’objets dans des ensembles comprenant jusqu’à 200 objets et vérifier son estimation en utilisant des stratégies de dénombrement.
Habileté : estimer le nombre d’objets
Une compréhension du concept de quantité est essentielle au développement de l’habileté à estimer, à juger de l’ordre de grandeur et à apprécier les relations de proportionnalité. Les élèves développent leur habileté à estimer en prenant conscience des relations qui existent entre les quantités (par exemple, Cette quantité est-elle plus proche de 10 ou de 20?) et en jugeant de l’ordre de grandeur. L’élève, par exemple, qui estime qu’il y a 100 jetons dans un ensemble, alors qu’il n’y en a en réalité que 40, n’a pas développé un bon sens de l’ordre de grandeur. Cependant, celle ou celui qui estime que l’ensemble contient 50 jetons en a un meilleur sens. On doit donc habituer les élèves, dès les premières années d’études, à questionner la vraisemblance de leurs estimations. Le matériel de manipulation (par exemple, cadres à dix cases) les aide à développer l’habileté à estimer, puisqu’il leur permet de visualiser les quantités.
Source : Guide d'enseignement efficace des mathématiques de la 1re à la 3e année, p. 45.
L’estimation est un processus par lequel des informations visuelles et mentales servent à évaluer l’ordre de grandeur d’une quantité. Les estimations tiennent une place importante dans nos communications quotidiennes, car elles nous donnent des quantités approximatives. Elles sont utilisées notamment par les médias (par exemple, près de 200 personnes étaient au rassemblement) ou par nous, dans nos échanges (par exemple, les achats à l’épicerie coûtent environ 200 $ par semaine).
À l’instar de l’enseignement des concepts mathématiques en général, l’estimation doit être exploitée en contexte de résolution de problèmes. Afin de bien faire comprendre aux élèves le concept d’estimation d’une quantité, il est même préférable de leur présenter des problèmes dans lesquels seule l’estimation est recherchée (par exemple, Environ combien de pages du dictionnaire dois-je lire pour parcourir les définitions de 100 mots?). Parfois, il peut être valable de comparer les estimations à la quantité exacte afin d’examiner l’efficacité des stratégies d’estimation et la précision des estimations. Toutefois, cette opération ne devrait pas s’effectuer systématiquement, faute de quoi les élèves ne verront pas la pertinence des estimations, puisque la réponse recherchée semble devoir être la quantité exacte.
Les élèves croient souvent qu’une estimation est une devinette ou encore qu’une seule estimation peut être considérée comme acceptable, alors que ce qui compte dans l’estimation, c’est l’ordre de grandeur et non le nombre. Une bonne estimation est un nombre qui définit grosso modo la quantité évaluée. Il est certain, toutefois, que l’efficacité à estimer démontre un bon sens du nombre. Il n’y a pas de règles définies pour y arriver ni de but à atteindre : le contexte de chaque problème et la grandeur des nombres détermineront le degré acceptable de précision. Une estimation, par exemple, d’environ 60 blocs ou d’environ 40 blocs est très acceptable lorsque la quantité réelle de blocs est de 50, alors qu’une estimation d’environ 200 serait le résultat d’une devinette ou d’une stratégie inefficace. En revanche, si la quantité réelle correspond à 175 blocs, des estimations d’environ 150 ou 200 deviennent acceptables, puisque l’écart entre l’estimation et la quantité exacte est négligeable compte tenu de la grandeur de la quantité réelle.
Dans des situations d’estimation, afin de préciser que le nombre représente une quantité approximative, il est important que les élèves communiquent l’estimation en utilisant un langage « d’approximation », tel que environ, au moins, près de, un peu plus de, à peu près, plus ou moins ou entre; par exemple, environ 100 personnes étaient présentes à la soirée, il mesure à peu près 1 m, c’est un peu moins de 5 kg, c’est un peu plus de 200 $, il faudra entre 4 et 5 heures de route. Ces stratégies pédagogiques permettent d’éloigner l’impression qu’il existe une seule et unique « bonne » estimation et de reconnaître la valeur des diverses estimations ainsi que leur degré de précision.
Afin d’estimer, il faut effectuer une comparaison entre la quantité à estimer et des repères; par exemple, Rachelle et Oman se demandent combien d’élèves jouent dans une partie spécifique de la cour d’école. En y réfléchissant, ils peuvent utiliser un repère comme le nombre d’élèves dans leur groupe-classe, soit 20 élèves. Cette situation réelle connue les aide à se représenter mentalement un certain nombre de personnes dans un espace donné et à estimer, soit qu’il y ait moins de 20 personnes sur le terrain ou, au contraire, qu’il s’y trouve entre 20 et 40 élèves (deux fois plus) ou près de 60 personnes (trois fois plus). Il est important de savoir qu’en estimant à l’aide de repères, les élèves appliquent un raisonnement proportionnel entre un montant connu (20 élèves dans un certain espace) et un montant inconnu (le nombre d’élèves dans un autre espace).
Il arrive que les élèves n’ont pas intégré de repères pour une situation donnée et doivent donc employer une autre stratégie. Elles et ils peuvent alors dénombrer un sous-ensemble d’objets et utiliser ce nombre comme repère pour estimer la quantité totale d’objets. Si, par exemple, on leur demande d’évaluer le nombre de billes dans un bocal, les élèves peuvent d’abord prendre une poignée de billes et les compter afin de pouvoir comparer cette quantité repère au contenu du bocal. Elles et ils pourraient aussi dénombrer les billes dans le fond du bocal (10 billes noires) et ensuite, estimer le nombre de rangs de billes dans le bocal (environ 9 rangs) pour être en mesure d’estimer le nombre total de billes dans le bocal (90 billes). Les élèves peuvent aussi séparer la quantité en sections et estimer la quantité dans chaque section.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 36 à 38.
Habileté : dénombrer (vérifier son estimation à l’aide de stratégies de dénombrement)
Dénombrer suppose à la fois de réciter une série de nombres (compter) et de les associer à une série d’objets.
Au moment de leur entrée en maternelle, les enfants ont habituellement déjà appris à compter et sont parfois capables de compter jusqu’à de grands nombres en faisant habituellement appel à leur mémoire et en récitant les nombres de manière continue, comme elles et ils le font avec les lettres de l’alphabet. Toutefois, si on leur demande quel est le nombre qui suit 5, elles et ils recommenceront peut-être à compter à partir de 1 sans vraiment saisir le sens de la question. Les jeunes enfants ne comprennent pas forcément que l’on compte toujours de la même manière. Quelques enfants, par exemple, comptent en disant « 1, 2, 3, 4, 5, 6, … » une fois et « 1, 2, 3, 5, 4, 6, 8, … » une autre fois, sans se soucier de cette incohérence. Si on leur demande de dénombrer des objets, elles et ils n’associeront pas forcément chaque objet à un chiffre du dénombrement ou toucheront peut-être à deux éléments en prononçant un seul chiffre (par exemple, quatorze), de sorte que le dénombrement ne donnera pas nécessairement le même résultat chaque fois. Les enfants ne comprennent parfois pas non plus que l’on peut dénombrer en même temps n’importe quel ensemble d’objets (même des objets très différents, comme des biscuits et des pommes) et que l’on peut commencer à dénombrer à partir de n’importe quel objet de l’ensemble et arriver au même nombre.
Source : Guide d'enseignement efficace des mathématiques de la 1re à la 3e année, p. 10.
Dénombrer implique d’être en mesure d’établir le lien entre une quantité et le nom ou le symbole du nombre qui la représente.
Une partie de la complexité de l’activité de dénombrement vient du fait qu’il faut établir un lien entre le nom ou le symbole d’un nombre et la quantité qu’il représente, lien que les enfants ne saisissent pas immédiatement (par exemple, le mot « cinq » et le symbole « 5 » représentent non seulement le 5e objet dénombré et le 5e chiffre dans l’ensemble des nombres qu’elles et ils ont appris à réciter, ils représentent aussi la quantité d’objets dénombrés). Il est essentiel que les enfants fassent ce lien entre la valeur quantitative d’un nombre et le rôle de celui-ci dans la séquence de dénombrement. Si on leur demande quelle est la quantité d’objets à la fin d’un dénombrement, quelques enfants recommenceront peut-être à dénombrer sans comprendre que le dernier nombre dit correspond en fait à la quantité d’objets dans l’ensemble.
Apprendre à compter jusqu’à de grands nombres est une expérience valable. Cependant, les enfants doivent d’abord développer une compréhension du concept de quantité et des relations entre les nombres en travaillant avec de petits nombres. Elles et ils peuvent en effet être capables de compter très loin tout en n’ayant encore qu’une connaissance limitée de la quantité représentée par le résultat d’un dénombrement; par exemple, elles et ils peuvent être capables de compter jusqu’à 30, mais être incapables de montrer 30 objets parmi un ensemble d’objets plus nombreux. Il faut donc offrir aux élèves de multiples occasions d’établir le lien entre le nom ou le symbole d’un nombre et la quantité que celui-ci représente.
Source : Guide d'enseignement efficace des mathématiques de la 1re à la 3e année, p. 11.
La présente section a pour objet d’aider le personnel enseignant à comprendre certains des concepts de base qui interviennent au début de l’acquisition de l’habileté à dénombrer. L’acquisition et la maîtrise de ces concepts ne se font pas forcément dans un ordre prédéterminé. Les élèves, par exemple, peuvent assimiler certaines parties d’un concept, passer à un autre, puis revenir au précédent.
La liste des concepts ci-dessous n’a pas pour but de présenter un cheminement que les élèves doivent suivre fidèlement. Il s’agit plutôt d’un outil pour aider le personnel enseignant à comprendre les éléments qui interviennent dans l’habileté à dénombrer. Il n’est pas nécessaire que les élèves des premières années d’études connaissent les noms de ces concepts.
Ordre stable : La séquence de dénombrement est stable et constante; on dit toujours, par exemple, « 1, 2, 3, 4, 5, 6, 7, 8 » et non « 1, 2, 3, 5, 6, 8 ».
Non-pertinence de l’ordre : Le dénombrement des objets d’un ensemble peut débuter avec n’importe quel objet de l’ensemble sans que la quantité totale change.
Invariance numérique : Une quantité peut être représentée par des choses différentes (par exemple, 5 peut être représenté par 5 objets identiques, par 5 objets différents, par 5 choses invisibles [5 idées] ou par 5 points sur une droite). L’invariance numérique est un concept complexe, mais la plupart des élèves le saisissent assez facilement.
Conservation du nombre : Le dénombrement d’un ensemble d’objets demeure le même, que ces objets soient dispersés ou rapprochés les uns des autres.
Correspondance de un à un : Lors d’un dénombrement, chaque objet est associé à un seul nombre. Au début, il est profitable pour les élèves de toucher chaque objet et de le mettre de côté une fois dénombré.
Cardinal d’un ensemble : Le cardinal d’un ensemble est le nombre d’éléments dans l’ensemble. L’élève qui dénombre de nouveau lorsqu’on lui demande combien il y a de bonbons dans un ensemble qu’elle ou il vient de dénombrer ne fait pas le lien entre le dénombrement et la quantité d’objets dans l’ensemble.
Un de plus, un de moins : À mesure que l’on avance dans une séquence de nombres, la quantité augmente d’un intervalle constant de 1 et à mesure que l’on recule dans la séquence, la quantité diminue de 1. Par extension, on inclut sous cet élément les intervalles de dénombrement autres que 1 (par exemple, si l’on compte par intervalles de 5, la quantité augmente de 5 tout le long de la séquence et si l’on compte à rebours par intervalles de 2, la quantité diminue de 2 tout le long de la séquence). Les élèves peuvent utiliser cet élément pour faciliter leur apprentissage des faits numériques de base; par exemple, en sachant que 4 + 4 = 8, elles et ils pourront apprendre que 4 + 5 = 9, puisque c’est 1 de plus.
Regroupement en fonction de la base dix : Le regroupement est le fait de rassembler les éléments d’un ensemble. Les regroupements faits en fonction de la base dix permettent aux élèves de mieux saisir le concept de valeur de position, concept à la base de l’écriture symbolique des nombres.
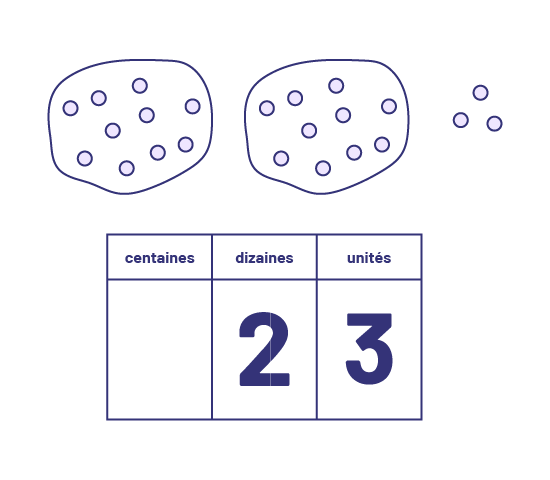
L’image montre deux dizaines de jetons regroupées par un cercle, et trois jetons hors des deux cercles. Sous les jetons, il y a un tableau séparé en trois : centaines, qui est vide, dizaines, qui contient le chiffre deux, et unités, qui contient le chiffre trois.
Source : Guide d'enseignement efficace des mathématiques de la 1re à la 3e année, p. 13 et 14.
