B1.5 Décrire les caractéristiques des nombres pairs et impairs.
Habileté : décrire les caractéristiques des nombres pairs et des nombres impairs
Les relations de divisibilité entre deux nombres sont des relations fondées sur la division. Par exemple, il y a une relation de divisibilité entre 6 et 2, puisque 6 est divisible par 2. L’étude de cette caractéristique des nombres naturels aide les élèves à développer leur sens du nombre et à mieux utiliser les nombres dans des situations quotidiennes.
Avec les élèves, il faut cependant éviter de s’attarder aux « trucs », à la terminologie et aux définitions. L’important pour les élèves, c’est de développer une compréhension conceptuelle de cette caractéristique à l’aide d’activités qui misent sur la reconnaissance des relations de divisibilité.
Si un nombre naturel est divisible en deux parties égales, c’est un nombre pair; sinon, c’est un nombre impair. La définition des nombres pairs et des nombres impairs est donc associée à la relation de divisibilité ou de non-divisibilité par deux.
C’est dans le cadre d’activités que les élèves devraient être amenées et amenés à constater que tous les nombres naturels ayant le chiffre 0, 2, 4, 6 ou 8 dans la position des unités sont des nombres pairs, alors que ceux ayant le chiffre 1, 3, 5, 7 ou 9 dans la position des unités sont des nombres impairs. Ces constats leur permettent, par la suite, de reconnaître rapidement si un nombre est pair ou impair sans avoir à vérifier la divisibilité par deux.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 55 et 56.
Les élèves peuvent utiliser du matériel de manipulation pour découvrir le lien qui existe entre les nombres pairs et la divisibilité par deux (par exemple, en tentant de répartir également un nombre pair ou un nombre impair de cubes entre deux élèves).
Source : Guide d'enseignement efficace des mathématiques de la 1re à la 3e année, p. 30.
Exemple
Karim dit que le nombre 26 est un nombre pair. A-t-il raison? Comment le sais-tu?
Stratégie 1
Partager une quantité en deux groupes égaux en utilisant du matériel de manipulation
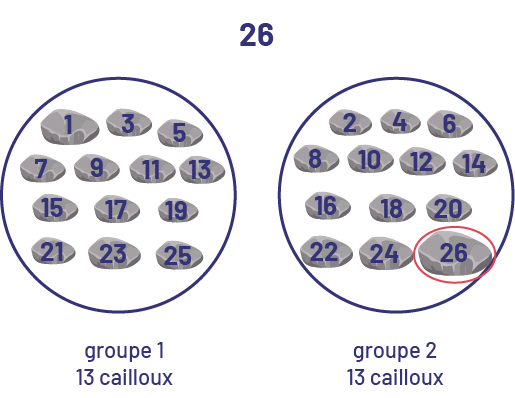
Le premier ensemble, nommé Groupe un, numérote ses cailloux avec des nombres impairs. Le deuxième ensemble, nommé Groupe deux, numérote ses cailloux avec des nombres pairs.
Je commence par compter 26 cailloux. Je place un caillou dans le groupe 1 et un autre dans le groupe 2. Je continue à partager tour à tour, les cailloux dans chaque groupe jusqu’à ce qu’ils soient tous placés. Je vois qu’il y a 13 cailloux dans chaque groupe, ce qui est une quantité égale. En séparant 26 objets en deux groupes égaux, je constate que 26 est un nombre pair.
Stratégie 2
Utiliser la régularité des nombres pairs et des nombres impairs et une droite numérique
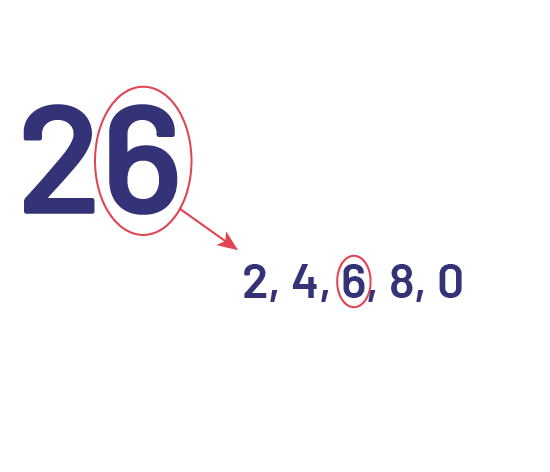
Je sais que les nombres qui ont 2, 4, 6, 8 ou 0 dans la position des unités sont des nombres pairs. Dans le nombre 26, le chiffre 6 est dans la position des unités, donc 26 est un nombre pair. Afin de vérifier, j’utilise une droite numérique et je compte par bonds de 2.

Des petits rectangles violets sont placés au-dessus de la droite pour marquer chaque bond de deux, avec la mention « plus deux ». Des flèches courbes pointillées illustrent chacun des bonds. Sur la droite, le nombre 26 est encerclé.
Source : En avant les maths!, 2e année, CM, Nombres, p. 3.
