B1.7 Reconnaître l’équivalence entre un tiers et deux sixièmes d’un même tout, dans des contextes de partage équitable d’une quantité.
Habileté : reconnaître l’équivalence
Reconnaître l’égalité de deux fractions, c’est reconnaître que les deux fractions représentent la même quantité.
Il est parfois difficile pour les élèves de saisir qu’une quantité peut porter plusieurs noms et être représentée par plusieurs nombres (par exemple, le nombre \(\frac{1}{3}\) représente la même quantité que le nombre \(\frac{2}{6}\); donc, on peut affirmer que \(\frac{1}{3}\ = \frac{2}{6}\)).
La compréhension des fractions équivalentes fait partie du raisonnement proportionnel que les élèves vont continuer à développer au cours des prochaines années d’études.
Déterminer des fractions équivalentes, c’est déterminer des fractions qui représentent la même quantité. On cherche alors un nombre de « petites parties » d’un tout qui correspondent à un nombre particulier de « grandes parties » du même tout. Si, par exemple, on cherche le nombre de sixièmes qui correspond à un tiers, on peut représenter les deux fractions à l’aide de modèles de surface identiques afin de reconnaître l’équivalence.
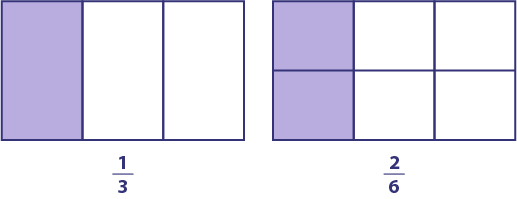
Le premier est divisé en trois parties égales sur le sens de la largeur, et en dessous, il est écrit « un tiers ». La première partie est colorée en violet tandis que les deux autres sont blanches. Le deuxième rectangle est divisé en six parties égales, deux rangées de trois carrés. En dessous, il est écrit « deux sixièmes ». Le premier carré du haut et le premier carré du bas sont colorés en violet.
La relation d’équivalence doit aussi être explorée par rapport aux fractions d’un ensemble. Dans l’image ci-dessous, les élèves voient aisément que \(\frac{2}{6}\) des bonbons sont emballés dans des papillotes rouges. Toutefois, elles et ils peuvent avoir de la difficulté à déterminer la fraction équivalente, soit \(\frac{1}{3}\). Il importe alors de présenter aux élèves des activités qui leur permettent de manipuler les éléments de l’ensemble. Ainsi, elles et ils peuvent les grouper en ensembles de 2 et déterminer la fraction équivalente.

\(\frac{2}{6}\) des bonbons sont emballés dans des papillotes rouges.
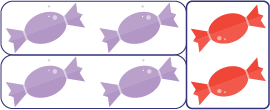
\(\frac{1}{3}\) des bonbons sont emballés dans des papillotes rouges.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 50 à 52.
Connaissance : fractions équivalentes
Deux fractions sont équivalentes si elles représentent la même quantité.
Note : En 2e année, il est important de souligner qu’il s’agit de fractions d’un même tout. Une même partie d’un tout peut être représentée par différentes fractions (par exemple, un tiers et deux sixièmes sont des fractions équivalentes).

À gauche de l’image, trois ensembles de quatre cœurs placés l’un sous l’autre sont encerclés. Dans le premier ensemble, les cœurs sont vert forêt. En dessous, il est écrit un tiers. Les cœurs des deux autres ensembles sont blancs. Ensuite, un trait sépare ces ensembles de six autres ensembles de cœurs à côté. Ils sont disposés en deux rangées de trois. Dans le premier ensemble du haut et le premier ensemble du bas, les cœurs sont vert forêt. En dessous, il est écrit un tiers. Les cœurs des quatre autres ensembles sont blancs. En haut à droite de l’image, il y a une droite numérique graduée de zéro à trois tiers. La section entre zéro et un tiers est surlignée en vert forêt. En dessous, il est écrit zéro vis-à-vis le zéro, un sixième entre zéro et un tiers, deux sixièmes vis-à-vis un tiers, trois sixièmes entre un tiers et deux tiers, quatre sixièmes vis-à-vis deux tiers, cinq sixièmes entre deux tiers et trois tiers, et six sixièmes vis-à-vis trois tiers.
Source : En avant les maths!, 2e année, CM, Nombres, p. 2.
