B2.1 Utiliser les propriétés de l’addition et de la soustraction, et les relations entre l’addition et la multiplication ainsi qu’entre la soustraction et la division pour résoudre des problèmes et vérifier la vraisemblance des calculs.
Habileté : utiliser les propriétés de l’addition et de la soustraction pour résoudre des problèmes et vérifier la vraisemblance des calculs
L’utilisation des propriétés des opérations et des relations entre les opérations nous permet de construire des phrases numériques et de les manipuler avec souplesse de manière à résoudre des équations et à simplifier des calculs.
(Department of Education and Training of Western Australia, First Steps in Mathematics: Number – Understand Operations, Calculate, Reason About Number Patterns, vol. 2, 2005, p. 66, traduction libre)
Au cycle primaire, les élèves établissent des liens entre les opérations en faisant diverses activités. Elles et ils connaissent, par exemple, le rôle du nombre zéro et savent que l’addition et la soustraction sont des opérations inverses et que l’addition est commutative. Avec le temps, les élèves développent leur sens du nombre et leur sens des opérations et s’en servent graduellement avant d’effectuer des opérations. Cette pratique, quoique souvent informelle et mentale, demeure toutefois essentielle à la compréhension des relations entre les nombres et entre les opérations.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 97.
Il n’est pas nécessaire que les élèves du primaire connaissent les noms des propriétés. Il suffit qu’elles et ils les utilisent naturellement pour combiner des nombres.
Les élèves montrent leur compréhension des propriétés des opérations mathématiques au moyen d’objets ou de nombres spécifiques et utilisent du matériel concret, des dessins, des mots ou des symboles pour représenter des idées mathématiques et des relations.
Source : Guide d'enseignement efficace des mathématiques de la maternelle à la 3e année, p. 17.
Les propriétés de l’addition sont :
- la commutativité (par exemple, \(1 + 2 = 2 + 1\));
- l’associativité (par exemple, \((8 + 9) + 2 = 8 + (9 + 2)\));
- le nombre zéro (0) en tant qu’élément neutre (par exemple, \(1 + 0 = 1\)).
La propriété de la soustraction est :
- le nombre zéro (0) en tant qu’élément neutre (par exemple, 1 - 0 = 1).
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 33.
La commutativité
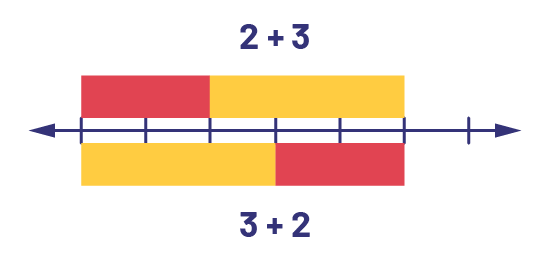
Les élèves qui reconnaissent la propriété de commutativité de l’addition peuvent réduire de moitié la quantité de faits numériques qu’il leur faut apprendre. La représentation visuelle de faits comme \(3 + 2\) et \(2 + 3\) aide les élèves à saisir cette relation.
Source : Guide d'enseignement efficace des mathématiques de la maternelle à la 6e année, p. 19.
 Image
Une ligne de dénombrement pointe à gauche comme à droite. Elle est divisée en six parts. En haut, il y a une réglette
rouge qui mesure deux parts, et une réglette jaune qui mesure trois parts. Il est écrit l’équation deux plus trois. En
bas, il y a une réglette jaune qui mesure trois parts et une réglette rouge qui mesure deux parts. Il est écrit
l’équation trois plus deux.
Image
Une ligne de dénombrement pointe à gauche comme à droite. Elle est divisée en six parts. En haut, il y a une réglette
rouge qui mesure deux parts, et une réglette jaune qui mesure trois parts. Il est écrit l’équation deux plus trois. En
bas, il y a une réglette jaune qui mesure trois parts et une réglette rouge qui mesure deux parts. Il est écrit
l’équation trois plus deux.
Associativité
L’associativité permet de combiner les termes d’une expression de différentes façons sans en modifier la valeur; par exemple, dans l’expression \(15 + 13 + 17\), il est possible d’associer 13 et 17 pour obtenir \(15 + (13 + 17)\), ce qui donne \(15 + 30\), soit 45. Il est aussi possible d’associer 15 et 13 pour obtenir \((15 + 13) + 17\), ce qui donne \(28 + 17\), soit 45.
L’associativité ne change pas l’ordre des nombres d’une expression numérique. On peut cependant jumeler l’associativité et la commutativité pour faciliter l’évaluation d’une expression numérique. Pour déterminer la valeur de l’expression \(19 + 27 + 11\), on peut déterminer celle de \((19 + 11) + 27\), car le 9 et le 1 sont complémentaires et donnent une dizaine, ce qui permet d’obtenir la réponse mentalement, soit \(30 + 27\). C’est en exposant les élèves à un grand nombre d’activités que l’enseignante ou l’enseignant les amène à comprendre et à utiliser les différentes propriétés avec efficacité.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 105 à 107.
Important!
Les parenthèses sont utilisées pour assurer l’exactitude mathématique du message. Cependant, avec les élèves de 2e année, il est préférable de s’en tenir à des façons moins abstraites de mettre en évidence les regroupements; par exemple :

Image Deux équations sont écrites l’une sous l’autre. Première équation : deux plus neuf plus cinq égale deux plus neuf plus cinq. Il y a un cercle autour de « deux plus neuf » avant le symbole « égal », ainsi qu’autour de « neuf plus cinq » après le symbole « égal ». La deuxième équation est introduite par la conjonction « ou » suivie de : deux plus neuf plus cinq égale deux plus neuf plus cinq. Il y a un trait souligné en arc qui relie deux et neuf avant le symbole « égal », et un autre qui relie neuf et cinq après le symbole « égal ».
Source : Guide d'enseignement efficace des mathématiques de la maternelle à la 3e année, p. 98.
Élément neutre (propriété du nombre 0 dans l’addition et la soustraction)
En ayant recours à la propriété du nombre 0, inciter les élèves à proposer des conjectures telles que : « Si j’ajoute zéro à une quantité (par exemple, \(5 + 0\)), cette quantité reste pareille et si j’ajoute une quantité quelconque à 0 (par exemple, \(0 + 5\)), j’obtiens la quantité ajoutée. »
En appliquant ces conjectures à différents nombres, les élèves seront en mesure de formuler une généralisation, à savoir que cette propriété du nombre 0 est vraie pour tous les nombres.
Pour le rôle du 0 dans la soustraction, inciter les élèves à proposer une conjecture telle que : « Lorsque je soustrais 0 d’un nombre (par exemple, \(5 - 0\)), j’obtiens le nombre de départ. » En appliquant cette conjecture à différents nombres, les élèves seront en mesure de formuler une généralisation, à savoir que cette propriété du nombre 0 est vraie pour tous les nombres.
Source : Guide d'enseignement efficace des mathématiques de la maternelle à la 3e année, p. 93 et 95.
Habileté : utiliser la relation entre l’addition et la soustraction pour résoudre des problèmes et vérifier la vraisemblance des calculs
L’addition et la soustraction
La compréhension des liens entre les opérations (par exemple, l’addition et la soustraction sont des opérations inverses) aide les élèves à apprendre les faits numériques de base et à résoudre des problèmes.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 32.
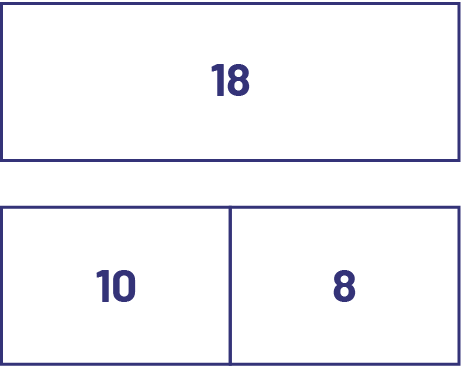
L’addition et la soustraction sont des opérations inverses. Les élèves qui sont en apprentissage ont souvent de la difficulté à résoudre des équations telles que \(17 \ + ? = 31\). Plusieurs enseignantes et enseignants les incitent à utiliser l’opération inverse, soit la soustraction. Or, il peut s’agir d’apprendre un truc, à moins que les élèves comprennent la raison pour laquelle la soustraction est une stratégie possible. Pour cela, elles et ils doivent d’abord saisir la relation du tout et de ses parties ainsi que le sens d’une différence; par exemple, un nombre peut être représenté comme suit :
 Image
L’image contient trois rectangles. Le premier, au-dessus des deux autres, contient le nombre 18. Collés ensemble, les
deux rectangles en dessous égalisent la longueur de celui du dessus. Ils présentent respectivement les nombres dix et
huit.
Image
L’image contient trois rectangles. Le premier, au-dessus des deux autres, contient le nombre 18. Collés ensemble, les
deux rectangles en dessous égalisent la longueur de celui du dessus. Ils présentent respectivement les nombres dix et
huit.
Cette façon de représenter la relation entre un nombre et ses parties permet de voir que la soustraction est l’opération inverse de l’addition. Ainsi, puisque \(10 + 8 = 18\) et que \(8 + 10 = 18\), donc \(18 - 10 = 8\) et \(18 - 8 = 10\). De plus, les élèves peuvent comprendre la raison pour laquelle l’addition est commutative (\(10 + 8 = 8 + 10\)) et que la soustraction ne l’est pas (\(18 - 10 ≠ 10 - 18\)). Les élèves qui ont acquis un bon sens du nombre et qui sont capables de décomposer et de regrouper des nombres peuvent mettre leurs connaissances à profit pour résoudre plus efficacement des équations telles que \(10 \ + \mathord{?} = 18\) en comprenant que l’on cherche la différence entre 10 et 18.
Source : Adapté du Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 97 et 98.
La multiplication et l’addition
Le lien entre la multiplication et l’addition est souvent le point de départ pour présenter aux élèves le concept de multiplication. Au début de l’apprentissage de la multiplication, les élèves reconnaissent que la situation présente « plusieurs fois » une même quantité et utilisent des groupes égaux pour représenter la situation et l’addition répétée pour obtenir la réponse.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 85.
Puisque la multiplication peut être perçue comme une addition répétée (par exemple, \(3 \times 5 = 5 + 5 + 5\)), les élèves peuvent faire le lien entre la stratégie des doubles (par exemple, \(4 + 4 = 8\)) et la multiplication par deux. Les liens entre l’addition et la multiplication peuvent aussi les aider à apprendre certains faits numériques de base; par exemple, l’élève qui sait que \(3 \times 4 = 12\) pourra apprendre que \(4 \times 4 = 16\), puisque \(4 \times 4 = 16\) équivaut à \((3 \times 4) + 4 = 16\).
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 32.
En résolvant une variété de problèmes et en discutant de stratégies, les élèves en viennent à établir et à saisir le lien entre le mot « fois » et le signe « \(\times\) », étape cruciale dans le développement de la compréhension de la multiplication. Une fois leur sens de la multiplication bien ancré, elles et ils auront recours plus régulièrement à l’opération de multiplication pour obtenir les réponses.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 86.
La division et la soustraction
Dans le même ordre d’idées, la division peut être associée à une soustraction répétée, mais pas de la même façon. Le produit d’une multiplication est égal à la somme résultant de l’addition répétée, alors que le quotient d’une division est égal au nombre de soustractions répétées (par exemple, pour calculer \(20 \div 5\), on fait \(20 - 5 = 15\), \(15 - 5 = 10\), \(10 - 5 = 5\), \(5 - 5 = 0\); on a soustrait quatre fois; donc \(20 \div 5 = 4\)).
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 98 et 99.
La division peut être perçue comme une soustraction ou une addition répétée (par exemple, \(24 - 4 - 4 - 4 - 4 - 4 - 4 = 0\), donc on peut soustraire 6 groupes de 4 pour obtenir 0 ou \(4 + 4 + 4 + 4 + 4 + 4 = 24\), donc cela prend 6 groupes de 4 pour faire 24) ou comme un partage en parts égales.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 32.
Il faut du temps pour que les élèves assimilent ces relations. Pour y parvenir, le personnel scolaire peut avoir recours à des activités concrètes, à la résolution de problèmes et à des échanges mathématiques orientés vers les liens entre les opérations.
Connaissance : la commutativité
Une opération est commutative si son résultat demeure inchangé lorsqu’on intervertit l’ordre des termes qui la composent. Par exemple, l’addition est commutative. Cependant, la soustraction n’est pas une opération commutative.
Exemple
\(2 + 3 = 3 + 2\)
\(6 - 3 ≠ 3 - 6\)
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 102.
Connaissance : l’associativité
L’associativité est une propriété de l’addition et de la multiplication. Elle permet de combiner les termes d’une expression de différentes façons sans en modifier la valeur.
Connaissance : rôle du nombre 0 dans l’addition et la soustraction
Comme son nom l’indique, un élément neutre est un nombre qui n’a aucun effet sur une opération donnée. Ainsi, le nombre 0 est l’élément neutre de l’addition (par exemple, \(7 + 0 = 7\) et \(0 + 7 = 7\)). Dans une soustraction, le nombre 0 ne produit aucun effet uniquement lorsqu’il est le deuxième terme (par exemple, \(3 - 0 = 3\)).
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 107.
Connaissance : relations entre l’addition, la soustraction, la multiplication et la division
L’addition et la soustraction sont des opérations inverses.
La multiplication peut être associée à une addition répétée.
La division peut être associée à une soustraction répétée.
