B2. Sens des opérations
Utiliser ses connaissances des nombres et des opérations pour résoudre des problèmes mathématiques de la vie quotidienne.
Situation d’apprentissage 1 : deux par deux
Durée totale : environ 2 heures
| Attente | Contenus d'apprentissage |
| B2. Sens des opérations Utiliser ses connaissances des nombres et des opérations pour résoudre des problèmes mathématiques de la vie quotidienne. |
B2.2 Se rappeler les faits d’addition et de soustraction de nombres jusqu’à 20 et les faits de la soustraction associés, et démontrer sa compréhension de ces faits.
B2.3 Utiliser des stratégies de calcul mental, y compris l’estimation, pour additionner des nombres naturels dont la somme est égale ou inférieure à 50 et pour soustraire des nombres égaux ou inférieurs à 50, et expliquer les stratégies utilisées. B2.4 Utiliser des objets, des schémas et des équations pour représenter, décrire et résoudre des situations relatives à l’addition de nombres naturels dont la somme est égale ou inférieure à 100 et à la soustraction de nombres égaux ou inférieurs à 100. |
Intention pédagogique
Cette situation a pour but de permettre à l’élève :- d’établir des relations entre les nombres;
- d’estimer la somme d’une addition de deux nombres à deux chiffres;
- de développer diverses stratégies de dénombrement pour additionner mentalement des nombres naturels à deux chiffres;
- de résoudre des problèmes reliés à une phrase mathématique.
| Contexte pédagogique | Préalables |
|---|---|
| Lorsque vient le temps d’effectuer les opérations arithmétiques de base, on présente trop souvent aux élèves un algorithme précis au lieu de leur laisser la liberté de procéder comme bon leur semble. Pour l’addition de nombres à deux chiffres, par exemple, la tradition voulait qu’on additionne d’abord la colonne des unités, puis celle des dizaines. Lorsqu’on laisse les élèves résoudre les problèmes à leur façon, certaines et certains commencent par la colonne des dizaines et passent ensuite aux unités parce que cela leur semble plus facile.
En 2e année, l’élève doit arriver à comprendre les concepts et les procédures associés aux opérations arithmétiques et doit pouvoir les appliquer dans un contexte de résolution de problèmes. Elle ou il lui faut saisir les notions reliées au regroupement et au partage des nombres et découvrir les régularités et les liens qui existent entre les opérations. L’élève qui, pour résoudre le problème \(100 - 1 = \mathord{?}\) applique machinalement une procédure, ne fait pas appel à son propre raisonnement. C’est en leur permettant de créer leurs algorithmes que les élèves apprennent à réfléchir, à concevoir leurs propres stratégies et à développer un bon sens du nombre. |
Dans cette situation d’apprentissage, l’élève doit pouvoir :
|
Matériel
Activité principale
- matériel de manipulation
- grande feuille de papier ou tableau blanc interactif
Activité supplémentaire 4
- annexe 2D.1 (Grille vierge) (une copie par élève ou par équipe de deux)
- tapis de valeur de position
- jetons (un par élève ou par équipe de deux)
Vocabulaire mathématique
stratégie, démarche, solution, algorithme
Avant l’apprentissage (mise en train)
Durée : environ 40 minutes
Grouper les élèves en équipes de deux.
Présenter aux élèves le problème suivant.
Vendredi prochain, c’est le dîner de pizza. La dernière fois que nous avons mangé de la pizza, nous en avons manqué. Il faut donc en commander un peu plus. Nous avions commandé 48 morceaux de pizza. Il nous en faut 13 de plus. Combien de morceaux de pizza devons-nous commander cette fois-ci?
Demander à quelques élèves d’expliquer, à tour de rôle, le problème dans leurs propres mots. Les aider à s’exprimer en leur posant les questions suivantes :
- Qu’est-ce que tu sais déjà?
- Qu’est-ce que tu cherches à savoir?
Allouer aux élèves du temps de réflexion afin que les membres de l’équipe s’entendent sur une stratégie pour résoudre le problème.
Observer les élèves pendant qu’elles et ils travaillent et noter les diverses stratégies de dénombrement employées.
Circuler dans la salle de classe et observer les équipes. Poser aux élèves les questions suivantes :
- Comment pouvez-vous utiliser ce que vous savez déjà pour résoudre le problème?
- Pourquoi avez-vous choisi ce matériel de manipulation?
- Comment faites-vous pour résoudre le problème?
- Pourriez-vous utiliser une autre stratégie de dénombrement pour résoudre le problème?
- Pouvez-vous démontrer que votre solution est correcte?
Allouer aux élèves suffisamment de temps pour qu’elles et ils puissent essayer plus d’une stratégie de dénombrement.
Demander aux élèves d’apporter le matériel de manipulation utilisé ou leur feuille de calcul et de s’asseoir en cercle.
Inviter les équipes, à tour de rôle, à expliquer la façon dont elles ont résolu le problème.
Encourager les élèves à expliquer leur stratégie en se servant du matériel utilisé ou des calculs qu’elles ont faits.
Inciter les autres élèves qui ont utilisé le même matériel, mais une stratégie de dénombrement différente, à expliquer leur propre démarche.
Établir, au fur et à mesure, une liste des stratégies de dénombrement sur une grande feuille de papier et illustrer les étapes pour chacune des solutions. Afficher cette liste de stratégies de dénombrement dans la salle de classe.
Exemples de stratégies de dénombrement pour résoudre le problème suivant :
\(38 + 13 \)
Stratégie de dénombrement 1
\(30 + 10 = 40\) (addition des dizaines);
\(8 + 2 = 10\) (regroupement des unités en dizaine);
\(40 + 10 = 50\);
Il reste 1 unité des 3 unités du nombre 13;
\(50 + 1 = 51\).
Stratégie de dénombrement 2
38, 39, 40 (addition de 2 unités à 38 pour obtenir 40, le 2 provient de 13, donc \(13 - 2 = 11\));
\(11 - 10 = 1\) (pour rendre le nombre 11 facile à manier);
\(40 + 10 = 50\) (addition de 10 parce que les dizaines sont faciles à additionner);
\(50 + 1 = 51\) (addition de l’unité restante).
Stratégie de dénombrement 3
\(38 + 10 = 48\) (addition des dizaines);
\(48 + 3 = 51\) (addition des unités restantes).
Poser aux élèves les questions suivantes :
- Quelles autres stratégies de dénombrement auriez-vous pu utiliser?
- Comment expliqueriez-vous votre stratégie de dénombrement à une personne qui était absente aujourd’hui?
Pendant l’apprentissage (exploration)
Durée : environ 40 minutes
Demander aux élèves de résoudre le problème individuellement.
Présenter aux élèves le problème suivant.
Nous avons besoin de livres pour effectuer une recherche sur les animaux. Nous avons trouvé 36 livres traitant des animaux dans la bibliothèque de la salle de classe. Nous en avons aussi trouvé à la bibliothèque de l’école. Nous avons 72 livres en tout pour effectuer notre recherche sur les animaux. Combien de livres avons-nous trouvés à la bibliothèque de l’école?
Donner aux élèves le temps de réfléchir à ce problème et de choisir la stratégie de dénombrement qui leur convient.
Inciter les élèves à se référer à la liste des stratégies de dénombrement affichée et à utiliser celles qu’elles et ils maîtrisent bien.
Circuler dans la salle de classe et poser aux élèves des questions pour stimuler leur réflexion; par exemple :
- Qu’est-ce que tu sais déjà?
- Qu’est-ce que tu cherches à savoir?
- Comment peux-tu utiliser ce que tu sais déjà pour résoudre le problème?
- Pourquoi as-tu choisi ce matériel de manipulation?
- Quelle stratégie de dénombrement vas-tu utiliser pour résoudre le problème?
- Peux-tu utiliser une autre stratégie de dénombrement pour résoudre le problème?
Inviter les élèves à faire part de leur démarche au groupe-classe.
Cocher les stratégies de dénombrement utilisées qui figurent sur la liste et y ajouter les nouvelles, s’il y a lieu.
Poser aux élèves la question suivante :
- Combien de livres de plus nous faut-il pour en avoir 100?
Suivre la même démarche que précédemment.
Après l’apprentissage (objectivation/transfert des connaissances)
Durée : environ 40 minutes
Rassembler les élèves pour la mise en commun.
Demander à quelques élèves de venir, à tour de rôle, résoudre le problème au tableau. S’assurer de choisir des élèves qui n’ont pas utilisé la même stratégie.
Poser aux élèves les questions suivantes :
- As-tu utilisé la même stratégie de dénombrement pour résoudre les deux problèmes? Pourquoi?
- Quelle stratégie de dénombrement as-tu choisie pour résoudre le premier problème? le deuxième problème?
- Pourquoi as-tu choisi ces stratégies de dénombrement?
- En quoi ta deuxième stratégie de dénombrement ressemble-t-elle à ta première? diffère-t-elle de ta première?
- Comment tes connaissances des unités et des dizaines t’ont-elles été utiles pour résoudre les problèmes?
Exemples de critères d’évaluation
L’élève :
- résout les problèmes et explique sa stratégie de dénombrement;
- justifie la stratégie de dénombrement utilisée pour résoudre le problème;
- additionne et soustrait des nombres à deux chiffres avec et sans regroupement.
Différenciation pédagogique
L’activité peut être modifiée pour répondre aux différents besoins des élèves.
| Pour faciliter la tâche | Pour enrichir la tâche |
|
|
Suivi à la maison
Montre-moi ce que tu sais!
Communiquer, dans un bulletin d’information destiné aux parents, aux tutrices et aux tuteurs, toutes les stratégies de dénombrement apprises en classe. Donner quelques exemples de problèmes que les élèves pourront essayer de résoudre à la maison à l’aide de différentes stratégies de dénombrement.
Activité supplémentaire 4
Le nombre mystère
Remettre une copie de la grille vierge (annexe 2D.1) et un jeton à chaque élève ou à chaque équipe de deux.
Demander aux élèves de placer leur jeton sur un nombre de départ, tel 54.
Dessiner une flèche ou une série de flèches sur une grille vierge.
Inviter les élèves à déplacer leur jeton, d’une case à la fois, selon l’ordre des flèches pour déterminer le nombre mystère choisi par le personnel enseignant.
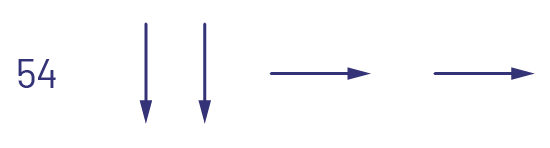
Note : La première flèche indique qu’il faut descendre d’une case, ce qui augmente le nombre de 10, pour arriver à 64. Il faut ensuite descendre d’une autre case jusqu’à 74, puis se déplacer d’une case vers la droite jusqu’à 75 et enfin d’une autre case pour arriver à 76, qui est le nombre mystère dans ce cas-ci. Le premier essai peut nécessiter une démonstration sur un tapis ou une grille de nombres.
Proposer aux élèves de choisir un nombre mystère, de l’écrire sur une feuille de papier et de fournir des indices, sous forme de flèches, à leur partenaire pour qu’elle ou il puisse le découvrir.
Demander aux élèves d’écrire la phrase mathématique qui correspond au parcours effectué pour découvrir le nombre mystère (par exemple, \(54 + 10 + 10 + 1 + 1 = 76\)).
Source: Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 137 à 144.
Situation d’apprentissage 2 : j’atteins la cible!
Durée totale : environ 2 heures
| Attente | Contenus d'apprentissage |
| B2. Sens des opérations Utiliser ses connaissances des nombres et des opérations pour résoudre des problèmes mathématiques de la vie quotidienne. |
B2.1 Utiliser les propriétés de l’addition et de la soustraction, et les relations entre l’addition et la multiplication ainsi qu’entre la soustraction et la division pour résoudre des problèmes et vérifier la vraisemblance des calculs. B2.2 Se rappeler les faits d’addition et de soustraction de nombres jusqu’à 20 et les faits de la soustraction associés, et démontrer sa compréhension de ces faits. |
Intention pédagogique
Cette situation a pour but de permettre à l’élève :
- de découvrir la relation qui existe entre l’addition et la soustraction;
- d’utiliser l’addition pour effectuer une soustraction.
| Contexte pédagogique | Préalables |
|---|---|
|
Pour comprendre l’addition et la soustraction, et les relations qui existent entre ces deux opérations, l’élève doit maîtriser le dénombrement et la décomposition des nombres en sachant répartir des quantités. L’élève qui sait décomposer des nombres, peut faire le lien entre l’addition et son opération inverse, soit la soustraction; par exemple, pour calculer 15 – 8, l’élève se demande « 15, c’est 8 plus quoi? ». Cette stratégie l’incite à se servir d’additions connues pour déterminer la quantité inconnue d’une soustraction. Une bonne compréhension de la relation qui existe entre l’addition et la soustraction est essentielle pour saisir le sens des opérations et maîtriser les faits numériques de base. |
Dans cette situation d’apprentissage, l’élève doit pouvoir :
|
Matériel
Activité principale
- annexe 2Rel.1 (Lance et compte!) (une copie par élève ou par équipe de deux)
- annexe 2Rel.2 (Bingo! et Nombre chanceux) (une copie par élève)
- grandes feuilles de papier
- matériel de manipulation (par exemple, cubes emboîtables, bâtonnets de bois)
- dés (deux par élève ou par équipe de deux)
- jetons bicolores (faces de couleur différente)
- gobelets en papier (un par élève ou par équipe de deux)
- cartes de nombres (quatre cartes de chaque nombre de 0 à 9) ou cartes à jouer (un jeu adapté par équipe de deux ou de quatre)
Activité supplémentaire 1
- feuilles de papier ou fiches de résolution de problèmes (une par élève) ou journal de mathématiques
- matériel de manipulation varié (raisins secs, jetons, bâtonnets de bois, etc.) (14 par élève)
Activité supplémentaire 4
- annexe 2Rel.5 (Découvrons les faits numériques de base) (quelques copies)
Vocabulaire mathématique
addition, soustraction, somme, différence, relation
Avant l’apprentissage (mise en train)
Durée : environ 30 minutes
Demander aux élèves de compléter les phrases suivantes :
- Additionner, c’est…
- Soustraire, c’est…
Inviter les élèves à partager leurs réponses et les écrire au fur et à mesure au tableau ou sur une grande feuille de papier.
Demander aux élèves de discuter de situations où il faut faire des additions et des soustractions, et de réfléchir aux ressemblances et aux différences qui existent entre elles.
Exemples
- Lorsque je joue aux billes, si je gagne j’additionne le nombre de billes à celles que j’ai déjà et, si je perds, je soustrais le nombre de billes perdues de mon ensemble de billes.
- Au marché, j’additionne les prix des articles que j’achète pour déterminer la somme à payer. Lorsque je paie, je soustrais cette somme du montant d’argent que je présente.
Écrire, au tableau ou sur une grande feuille de papier, trois nombres ayant une relation entre eux (par exemple, 5, 7 et 12).
Demander aux élèves de réfléchir aux relations qui existent entre ces nombres et à la façon de représenter cette relation par une addition et une soustraction (par exemple, \(5 + 7 = 12\), \(7 + 5 = 12\), \(12 - 7 = 5\), \(12 - 5 = 7\)).
Inciter les élèves à utiliser du matériel de manipulation pour explorer et représenter ces relations.
Donner aux élèves d’autres exemples semblables et les encourager à écrire les additions et les soustractions qui décrivent les relations existantes entre les trois nombres donnés.
Pendant l’apprentissage (exploration)
Durée : environ 60 minutes
Organiser les jeux ci-dessous pour permettre aux élèves de découvrir les relations qui existent entre l’addition et la soustraction.
Lance et compte!
Faire faire cette activité individuellement ou en équipe de deux.
Remettre à chaque élève ou à chaque équipe une copie de l’annexe 2Rel.1, un gobelet, deux dés et des jetons bicolores.
Expliquer aux élèves les étapes à suivre :
- Lancer les dés et trouver la somme des deux nombres obtenus.
- Déposer le même nombre de jetons bicolores dans un gobelet.
- Agiter le gobelet et lancer les jetons afin d’obtenir une combinaison de deux couleurs (par exemple, 11 jetons : 4 faces rouges et 7 faces jaunes).
- Écrire quatre phrases mathématiques, sur sa fiche de travail, pour décrire la combinaison de couleurs obtenue (par exemple, \(7 + 4 = 11\), \(4 + 7 = 11\), \(11 - 7 = 4\), \(11 - 4 = 7\)).
Demander aux élèves d’expliquer ce que leur a appris cette activité.
J’atteins la cible
Préparer le matériel requis pour l’activité, soit un jeu de 40 cartes de nombres (4 cartes de chaque nombre de 0 à 9) par équipe. Il est aussi possible d’utiliser un jeu de cartes en l’adaptant ainsi : prendre les cartes de l’as au valet et préciser que les as valent 1 et que les valets valent 0.
Grouper les élèves en équipes de deux ou de quatre.
Demander à une ou à un élève de distribuer six cartes à chaque membre de son équipe et de poser les cartes restantes au centre de la table, face vers le bas.
Expliquer aux élèves les étapes à suivre :
- Une ou un élève lance les dés et trouve la somme des deux nombres obtenus. Ce nombre devient la cible à atteindre pour cette partie.
- À tour de rôle, chaque élève examine ses cartes pour déterminer deux nombres pouvant être additionnés ou soustraits afin d’obtenir le nombre cible.
- L’élève qui peut « atteindre la cible » montre ses deux cartes aux autres et explique la façon de les additionner ou de les soustraire pour obtenir le nombre cible. Si tous les membres de l’équipe sont d’accord, l’élève met ses deux cartes de côté et en prend deux autres dans la pile au centre. L’élève qui ne peut pas « atteindre la cible » avec les cartes que l’élève a en main passe son tour.
- Lorsque tout le monde a joué, les élèves gardent leurs cartes et lancent les dés de nouveau pour déterminer un nouveau nombre cible.
- Le jeu se poursuit ainsi jusqu’à ce qu’il n’y ait plus de cartes au centre de la table.
Circuler dans la salle de classe et observer les élèves en train de jouer.
Guider les élèves qui ont du mal à trouver des additions ou des soustractions avec leurs cartes à l’aide de questions ou de directives, telles que :
- Je vois que tu as un 5. Quel autre nombre peux-tu y ajouter pour obtenir 9?
- Est-ce que tu peux utiliser le 8 pour faire une soustraction afin d’atteindre le nombre cible?
- Refais ton calcul pour vérifier si cette somme ou cette différence est juste.
Après l’apprentissage (objectivation/transfert des connaissances)
Durée : environ 30 minutes
Rassembler les élèves et leur poser les questions suivantes :
- Était-il difficile de penser à la fois à des additions et à des soustractions? Pourquoi?
- Était-il plus facile de penser à des additions ou à des soustractions? Pourquoi?
- Quelle relation y a-t-il entre l’addition et la soustraction?
- À mesure que le jeu progressait, est-ce que les tours allaient plus vite ou plus lentement? Pourquoi?
Inviter les élèves à noter leurs réflexions dans leur journal de mathématiques.
Exemples de critères d’évaluation
L’élève :
- explique la relation qui existe entre l’addition et la soustraction;
- utilise l’addition pour effectuer une soustraction;
- explique la ou les stratégies qui lui ont permis de résoudre les diverses opérations.
Différenciation pédagogique
L’activité peut être modifiée pour répondre aux différents besoins des élèves.
| Pour faciliter la tâche | Pour enrichir la tâche |
|
Utiliser des dés non numérotés sur lesquels il est possible d’écrire de plus grands nombres (par exemple, 4, 5, 6, 7, 8, 9). |
Suivi à la maison
Bingo! et Nombre chanceux
À la maison, l’élève peut jouer aux jeux Bingo! et Nombre chanceux.
Jouer quelques fois en classe afin que les élèves se familiarisent avec les règles des jeux.
Remettre à chaque élève une copie de l’annexe 2Rel.2 afin qu’elle ou il puisse jouer à ces jeux avec un membre de sa famille.
Activité supplémentaire 1 : La relation entre l’addition et la soustraction
Formuler des problèmes semblables à celui ci-dessous pour explorer la relation entre la soustraction et l’addition.
Ahmed a 6 raisins secs dans son assiette. Comme il a faim, son papa lui en donne quelques-uns de plus. Ahmed a maintenant 14 raisins. Combien de raisins secs son papa lui a-t-il donnés?
Demander aux élèves de trouver la solution en pensant à une addition.
Poser aux élèves la question suivante : Quel nombre peut-on ajouter à 6 pour obtenir 14?
Proposer aux élèves d’utiliser du matériel de manipulation et leur demander d’écrire leur démarche sur une feuille.
Activité supplémentaire 2 : Découvrons les faits numériques de base
S’inspirer des cartes de l’annexe 2Rel.5 pour en fabriquer plusieurs.

Grouper les élèves en équipes de deux. Remettre quelques cartes à chaque équipe.
Expliquer le jeu aux élèves : un membre de l’équipe cache un nombre avec son pouce ou un jeton et demande à sa ou à son partenaire de deviner le nombre dont il s’agit. Les rôles sont ensuite inversés.
Source: Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 155 à 161.
