B2.6 Représenter la multiplication de nombres jusqu’à 10 × 10 et la division de nombres jusqu’à 100 ÷ 10, à l’aide d’une variété d’outils et de schémas, y compris des dispositions rectangulaires.
Activité 1 : des fois à l’envers? (disposition rectangulaire)
Démarche
Demander aux élèves de représenter \(5 \times 8 \) et \(8 \times 5 \) à l’aide de dispositions rectangulaires.
Voici des représentations possibles :
Image 4 dispositions rectangulaires : La première représente 5 multipliés par 8, disposée comme suit : 5 colonnes de 8 jetons. La deuxième représente 8 multipliés par 5, disposée comme suit : 8 colonnes de 5 jetons. La troisième représente 8 multipliés par 5, disposée comme suit, 8 rangées de 5 jetons. La quatrième représente 5 multipliés par 8, disposée comme suit : 5 rangées de 8 jetons. Procéder de la même façon avec diverses multiplications de 2 nombres.
Intervention
Poser des questions pour faire comprendre la commutativité de la multiplication telles que :
- Que vois-tu?
- Combien y a-t-il de jetons? de rangées? de colonnes?
- Je tourne la disposition rectangulaire (90°). Combien y en a-t-il maintenant?
- Quel est le produit de 5 et 8? Quel autre fait de multiplication lui ressemble?
- En tournant les dispositions rectangulaires, quelles autres paires de nombres donnent le même produit?
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 42.
Activité 2 : dispositions rectangulaires recherchées
Choisir un nombre ayant plusieurs facteurs, tels 12, 18, 24 ou 36.
Projeter les dispositions rectangulaires possibles pour représenter un nombre. Par exemple, si on choisit 18, il est possible de disposer 18 jetons en rangées et en colonnes comme suit : \(1 \times 18 \), \(2 \times 9 \), \(3 \times 6 \), \(18 \times 1 \), \(9 \times 2 \) et \(6 \times 3 \).
Expliquer la relation entre les dispositions rectangulaires telles que \(6 \times 3 \) et \(3 \times 6 \) (le produit est le même, mais la disposition des rangées et des colonnes est inversée) et que l’on appelle cette propriété de la multiplication la commutativité.
Demander aux élèves d’utiliser des jetons pour créer le plus de dispositions rectangulaires possible pour représenter le nombre 12.
Faire écrire les phases mathématiques pour représenter chacune des dispositions rectangulaires créées. Par exemple, les élèves peuvent écrire les phrases mathématiques suivantes, si les jetons sont disposés en 6 rangées et 2 colonnes :
\(2 \times 6 = 12 \)
\(6 \times 2 = 12 \)
\(2 + 2 + 2 + 2 + 2 + 2 = 12 \)
\(12 \div 2 = 6 \)
\(12 \div 6 = 2 \)
Dresser, pour chaque nombre choisi, une liste des phrases mathématiques écrites par les élèves. Faire ressortir comment la disposition rectangulaire représente chacune des phrases mathématiques.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 206-207.
Activité 3 : les dispositions rectangulaires
Demander aux élèves de trouver des objets qui rappellent une disposition rectangulaire dans la classe ou dans l’école (par exemple, carrelage, fenêtres, pupitres dans la classe).
Leur demander d’écrire des phrases mathématiques qui correspondent à ces dispositions rectangulaires et les inscrire au TBI ou sur une grande feuille de papier.
Leur soumettre des problèmes portant sur diverses dispositions rectangulaires. Par exemple :
- Quelles sont toutes les façons possibles de disposer 24 chaises en rangées et en colonnes?
- Comment peut-on placer 12 dessins sur un babillard sous forme de dispositions rectangulaires?
Demander aux élèves :
- de résoudre les problèmes en utilisant du matériel de manipulation;
- de noter leurs solutions et de composer des phrases mathématiques représentant leurs dispositions rectangulaires.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 207.
Activité 4 : jeu d’opérations
Former des équipes de 2 ou 3 et distribuer 2 dés et des jetons à chacune.
Demander aux élèves de lancer les 2 dés à tour de rôle et préciser que les nombres obtenus représentent le nombre de rangées et de colonnes d’une disposition rectangulaire (par exemple, si l’élève obtient un 3 et un 5, elle ou il fait une disposition rectangulaire de 3 rangées et de 5 colonnes ou de 5 rangées et de 3 colonnes).
Demander aux élèves d’écrire 3 phrases mathématiques en utilisant différentes opérations correspondant à la disposition rectangulaire représentée et de les expliquer (par exemple, \(5 + 5 + 5 = 15 \), \(3 \times 5 = 15 \) et \(15 \div 3 = 5 \)).
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 208.
Activité 5 : des jetons en disposition rectangulaire
Former des équipes de 2 et remettre à chacune un sac contenant 30 jetons et un jeu de cartes préparé à l’aide de l’annexe 3Rel.1 (Cartes de nombre).
Demander aux élèves :
- de tirer une carte du sac;
- de représenter, à l’aide de jetons, le nombre sous forme de disposition rectangulaire;
- de placer des crayons, des pailles ou des bouts de ficelle sur la disposition rectangulaire de façon à représenter des groupements égaux de jetons;
- de représenter d’autres groupements possibles.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 205.
Activité 6 : trios (commutativité)
Matériel
Cette activité se fait avec toute la classe. Chaque élève reçoit une carte du jeu des Trios. Une fois les cartes distribuées, les élèves cherchent les autres membres de leur trio. Il leur faut connaître la réponse à la question, ou envisager les questions possibles si leur carte porte une réponse. Par exemple, les trios pourraient être \(3 \times 6 \), \(6 \times 3 \) et 18. Lorsqu’un trio est complet, les 3 élèves s’assoient ensemble. Une fois que tous les élèves sont assis, chaque trio présente les cartes de commutativité à la classe.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 78.
Activité 7 : disposition rectangulaire (faits de multiplication)
Représenter, avec les élèves, les faits numériques de base à l’étude à l’aide des dispositions rectangulaires. Créer collectivement une grande affiche qui illustre les faits numériques de base.
L’affiche peut être créée avec différentes couleurs.
Demander aux élèves d’identifier des régularités et des liens entre les produits.
La table de multiplication est représentée de 2 façons.
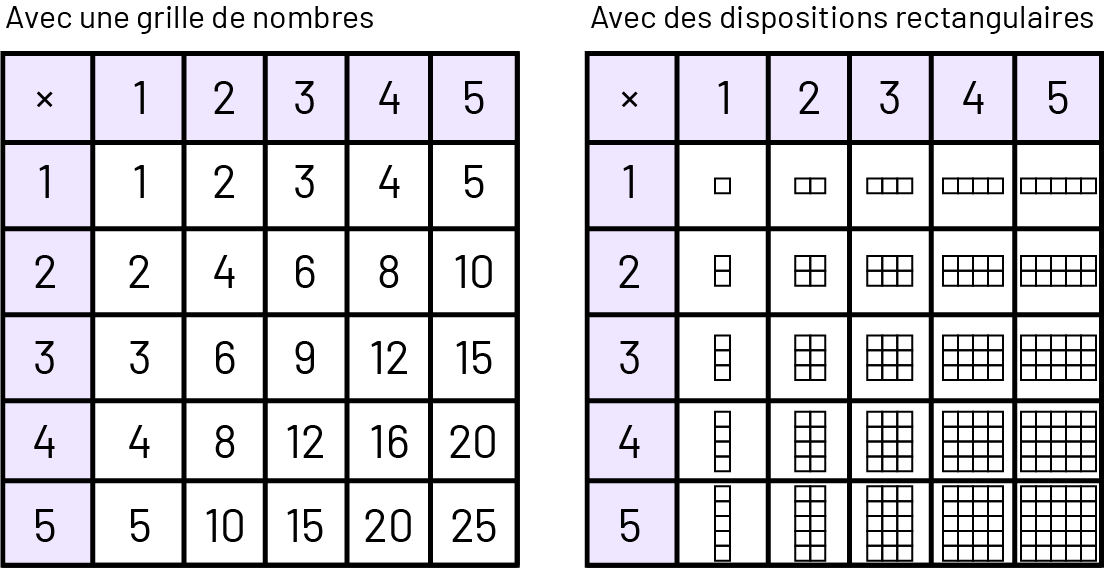Image Grille de nombres des multiplications de, un, 2, 3, 4, 5 par un, 2, 3, 4, 5. Grille de multiplication de nombres un, 2, 3, 4, 5 par un, 2, 3, 4, 5. Le résultat des multiplications est représenté
par des dispositions rectangulaires.
Source : L’@telier - Ressources pédagogiques en ligne (atelier.on.ca).