B1.1 Lire, représenter, composer et décomposer les nombres naturels de 0 jusqu’à 1 000, à l’aide d’une variété d’outils et de stratégies, et décrire de quelles façons ils sont utilisés dans la vie quotidienne.
Habileté : lire les nombres naturels
La lecture des nombres permet de les interpréter comme des quantités lorsqu’ils sont exprimés en mots ou en chiffres, ou représentés à l’aide de matériel concret ou de modèles.
Une quantité décrit un ordre de grandeur (le « nombre de » ou le « combien y-t-il de ») et constitue un concept essentiel au développement du sens du nombre.
Lorsque les tout-petits apprennent à compter, ils ne font pas immédiatement de lien entre les nombres récités et la notion de quantité. Ensuite, lorsqu’elles et ils apprennent à dénombrer, elles et ils associent machinalement chaque nombre 1, 2, 3, 4, 5 à l’un des objets dans un ensemble d’objets donné sans nécessairement saisir que 5, le résultat du dénombrement, correspond aussi à la quantité d’objets dans l’ensemble. Le lien entre la quantité et le nombre qui la représente est fort complexe. Un même nombre, par exemple 2, peut décrire des réalités très différentes. Il peut représenter à la fois 2 pommes, 2 pains ou encore 1 pomme et 1 pain. Il peut représenter aussi bien 2 gros ballons que 2 petits ballons. Ainsi, même si les ensembles d’objets sont différents, la quantité d’objets dans chacun des ensembles est la même. La complexité est accrue lorsque la quantité fait référence à une mesure (par exemple, longueur, masse, capacité) puisque les « objets quantifiés », c’est-à-dire les unités de mesure (par exemple, cm, kg, ml), ne sont pas manipulables comme le sont, par exemple les pommes, les pains ou les ballons.
Il est important de saisir la notion de quantité pour comprendre le concept de valeur de position.
Le concept de quantité intervient dans la compréhension du concept de valeur de position des chiffres qui composent un nombre. Cette valeur augmente successivement d’un facteur 10 lorsqu’on lit les chiffres de droite à gauche et diminue d’un facteur 10 lorsqu’on les lit de gauche à droite. La compréhension du concept de valeur de position s’avère aussi très utile lorsque les élèves commencent à utiliser des nombres plus grands ou des nombres décimaux.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 44-45.
Développer une compréhension conceptuelle du dénombrement a un lien direct avec la compréhension de la quantité et la valeur de position
En dénombrant dans le cadre d’activités concrètes, les élèves acquièrent les concepts et les stratégies de base qui les aident à comprendre la valeur quantitative du nombre. Les élèves apprennent à compter avec précision, à reconnaître les régularités dans le système de numération en base 10 (par exemple, 11, 12, 13…; 21, 22, 23…; 31, 32, 33…) et à faire des liens entre ces régularités et la valeur de position des chiffres qui composent les nombres. Le personnel enseignant doit tenir compte du fait que certains nombres sont particulièrement difficiles à apprendre en français. Il suffit de penser par exemple à un nombre comme 12, que certains élèves appelleront spontanément « dix-deux » ou aux nombres 70, 80 et 90, qui devraient logiquement se nommer « septante », « huitante » et « neufante ».
Exemple 1
Aider les élèves à apprendre le nom des nombres de 11 à 16 et à reconnaître qu’ils ne suivent pas la régularité des nombres de 20 à 69 (par exemple, vingt et un, trente et un, quarante et un). Leur faire remarquer par exemple que les nombres de 11 à 16 sont formés à partir des nombres de 1 à 6 et que certains commencent par les mêmes lettres (deux et douze; trois et treize; quatre et quatorze; six et seize).
Exemple 2
Aider les élèves à repérer dans une grille de nombres des régularités telles que :
- Le chiffre 9 termine toujours la dizaine (par exemple, 29, 39, 49).
- Dans la suite 10, 20, 30…, le chiffre des dizaines suit la même séquence que 1, 2, 3…
- La suite de nombres à l’intérieur de chaque dizaine est formée à partir de 1, 2, 3… (par exemple, 20 se combine à 1 pour devenir 21, puis à 2 pour devenir 22 et ainsi de suite).
- Les nombres pairs se terminent toujours par le chiffre 0, 2, 4, 6 ou 8.
- Les nombres impairs se terminent toujours par le chiffre 1, 3, 5, 7 ou 9.
Éléments sous-jacents
Selon les écrits les plus récents en éducation, les éléments suivants sont considérés comme des fondements au développement du concept de quantité.
Conservation du nombre
Le dénombrement d’un ensemble d’objets demeure le même, que ces objets soient dispersés ou rapprochés les uns des autres.
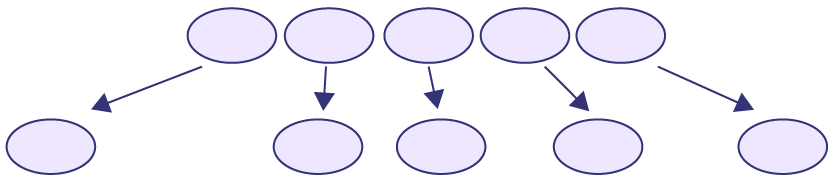 Image
Exemple de dénombrement avec des objets. 5 ovales sont côte à côte sur une ligne. Des flèches partent de chaque ovale.
La première et les dernières flèches écartent les ovales des deux bouts du reste du groupe. Les autres ovales
s’écartent légèrement les uns des autres.
Image
Exemple de dénombrement avec des objets. 5 ovales sont côte à côte sur une ligne. Des flèches partent de chaque ovale.
La première et les dernières flèches écartent les ovales des deux bouts du reste du groupe. Les autres ovales
s’écartent légèrement les uns des autres.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 12-13.
Reconnaissance globale d’une quantité
L’habileté à reconnaître globalement une quantité est l’habileté à quantifier les éléments d’un ensemble d’objets donné sans dénombrer chacun des éléments. Les activités conçues pour développer cette habileté (par exemple, à l’aide de cartes à pois) aident les élèves à acquérir une représentation mentale de la quantité associée à un nombre.
Cartes à pois
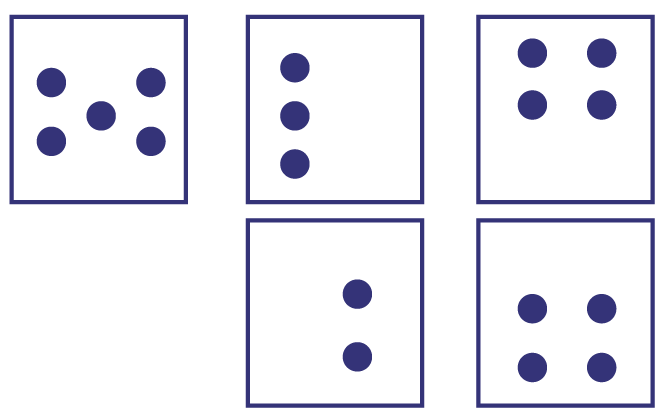
Image Des cartes à pois sont disposées sur 2 lignes. La première ligne à 3 cartes et la deuxième à 2 cartes. Carte un : 5 pois sur 3 colonnes de 2pois, un pois et 2 pois. Carte 2 : 3 pois sur une colonne sur la gauche de la carte. Carte 3 : 4 pois, sur 2 colonnes de 2 pois, sur le haut de la carte. Carte 4 : 2 pois sur une colonne. Carte 5 : 4 pois, sur 2 colonnes de 2 pois sur le bas de la carte.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 46.
Points d’ancrage
Les élèves prennent conscience des relations entre les nombres dès qu’ils commencent à compter sur leurs doigts. C’est alors qu’ils découvrent les relations qui existent entre les nombres de 1 à 4 et le nombre 5, et les nombres de 1 à 9 et le nombre 10. La compréhension de ces relations les aide à reconnaître, par exemple, que dans un cadre à 10 cases où l’on a posé des jetons sur toutes les cases sauf sur une, on a représenté le nombre 9.
Cette compréhension est par la suite élargie, d’abord aux relations entre les nombres de 0 à 10 et les points d’ancrage 5 et 10, et ensuite aux nombres plus grands.
Comprendre les relations entre les nombres et les points d’ancrage 5 et 10 aide les élèves à mieux saisir le concept de valeur de position. En regroupant des cubes emboîtables ou des centicubes, les élèves découvrent les relations entre les unités et les dizaines, et entre les dizaines et les centaines. Il importe de souligner que tout ce matériel de manipulation aide les élèves à développer leur compréhension du concept de valeur de position dans la mesure où elles et ils ont l’occasion de l’utiliser dans le cadre d’activités bien structurées. Rien ne sert au personnel enseignant de simplement modeler l’utilisation du matériel sans donner aux élèves la possibilité de le manipuler eux-mêmes et de développer le concept par leurs propres moyens. Cela reviendrait à leur faire apprendre un algorithme par cœur sans le comprendre.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 63-64.
Habileté : représenter les nombres naturels
Les élèves doivent apprendre à représenter les nombres de diverses façons et à les reconnaître sous leurs multiples représentations. Ces habiletés les aident à établir des liens entre un nombre, sa représentation et la quantité qu’il représente. Il est donc essentiel que les élèves soient exposés à différentes représentations des nombres. Il importe aussi que les élèves soient exposés à divers contextes qui les mènent à représenter un nombre selon chacun des modes de représentation illustrés dans le schéma suivant ainsi qu’à passer d’un mode de représentation à un autre.
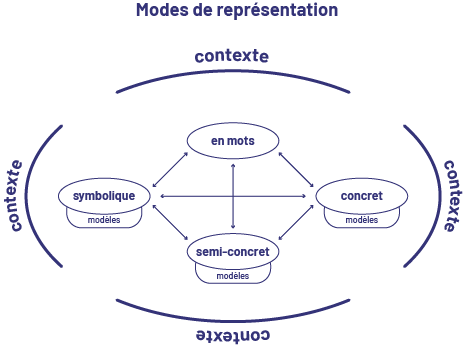
Le personnel enseignant doit être conscient de l’ordre dans lequel il exploite ces 4 modes de représentation avec les élèves. Baroody et Coslick (1998, p. 3-8 à 3-16) suggèrent de présenter un nouveau concept dans un contexte réel et significatif pour que les élèves puissent d’abord se créer des représentations à l’aide de mots, puis des représentations concrètes et semi-concrètes. Ce n’est que lorsque les élèves auront développé une certaine compréhension du concept qu’elles et ils pourront passer à sa représentation symbolique. Les élèves doivent être en mesure d’établir des liens entre les représentations et de passer aisément d’une représentation à une autre.
Représentations à l’aide de mots
En 3e année, les élèves apprennent à lire et à écrire en lettres les nombres jusqu’à 1 000. Il ne faut pas sous-estimer les défis que pose l’écriture des nombres en lettres. Pour aider les élèves à surmonter ces défis, le personnel enseignant devrait inclure les nombres au mur de mots et construire avec eux des référentiels pour résumer les règles d’accord en nombre de vingt, cent et mille.
Représentations concrètes
L’utilisation du matériel de manipulation (par exemple, jetons, matériel de base 10) pour représenter des nombres aide les élèves à développer le sens du nombre.

Une mise en garde s’impose lorsqu’il est question d’utiliser le matériel de manipulation. Il importe de reconnaître que ce matériel permet de représenter un concept mathématique, ce n’est pas le concept lui-même; par exemple, la planchette n’est pas une centaine, mais elle représente une centaine de petits cubes.
Le danger est que les élèves utilisent le matériel de façon mécanique sans faire les liens avec les concepts mathématiques sous-jacents. C’est pourquoi, le personnel enseignant doit s’assurer qu’il y a vraiment apprentissage et non pas seulement une utilisation aveugle du modèle. Par exemple, il est facile pour les élèves de remplir les espaces dans la phrase ci-dessous en regardant le tapis de valeur de position.

La représentation est ____ centaine(s), ____dizaine(s) et ____ unité(s).
Mais comprennent-ils qu’il y a aussi 235 petits cubes ou unités sur le tapis et que c’est une des réalités qui sont représentées par le nombre 235? Il est important de demander aux élèves d’expliquer de différentes façons ce qui est représenté. Par exemple, 235, c’est aussi 23 dizaines d’unités et 5 unités ou encore 2 centaines d’unités et 35 unités.
Une autre façon de vérifier la compréhension est de demander par exemple aux élèves combien il y a de dizaines dans 235. Plusieurs élèves auront tendance à dire qu’il y en a 3. Il importe alors de préciser que le chiffre dans la position des dizaines est un « 3 », mais que le nombre 235 est composé de 23 dizaines (23 regroupements de 10 unités = 230). On peut « voir » ces 23 dizaines en décomposant les 2 planchettes en 20 bâtonnets que l’on ajoute aux 3 bâtonnets qui sont dans la colonne des dizaines.
En utilisant le tapis de valeur de position, on remarque que même si les nombres s’écrivent de gauche à droite, ils sont formés de droite à gauche : les unités regroupées forment les dizaines, les dizaines regroupées forment les centaines, et ainsi de suite. Mais, une fois le dénombrement terminé, on écrit le nombre en partant de la gauche.

Le choix du matériel mis à la disposition des élèves peut aussi faire une différence dans le niveau de compréhension des concepts. On trouve sur le marché une variété de matériels pour représenter les nombres : billes, cubes emboîtables ou tout autre objet pouvant être utilisé pour dénombrer. Certains de ces matériels représentent clairement et concrètement la relation de grandeur entre les unités, les dizaines, les centaines… (par exemple, le matériel de base 10 utilisé dans les photos précédentes). Cependant, avec d’autres matériels, cette relation est représentée de façon plus abstraite. Par exemple, sur un abaque ou un « compteur de points », le groupement est représenté en fonction de la position du chiffre de gauche à droite, comme dans l’écriture symbolique des nombres.

Image Photo un : un abaque ou boulier. Des boules de différentes couleurs peuvent être déplacées sur des tiges de métal. Photo 2 : un compteur de points. Des plaquettes de couleurs sont placées en position ordonnée et peuvent être tournées les uns après les autres.
En exposant les élèves à une variété de matériels de manipulation, le personnel enseignant peut les aider à développer une meilleure compréhension des nombres.
Représentations semi-concrètes
Les élèves peuvent aussi représenter les nombres avec du matériel semi-concret (par exemple, illustration, grille de nombres, droite numérique).
Illustration : Un nombre peut être représenté par des dessins de façon à illustrer certains regroupements. Par exemple, le nombre 376 peut être illustré par regroupements de 50 comme suit :
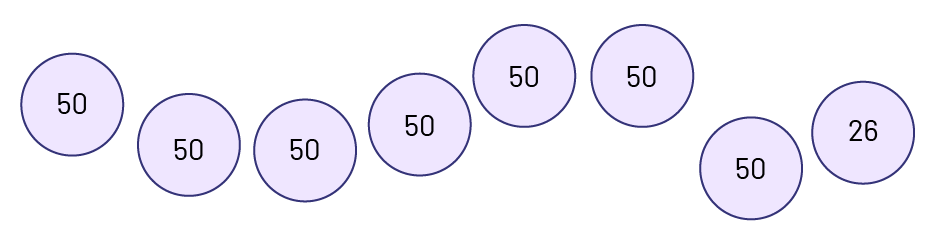
Son illustration peut aussi être en lien avec le matériel de manipulation.

Grille de nombres : La grille de nombres jusqu’à 100 est très utilisée au cycle primaire. Quoique plus difficile à manipuler, une grille de 1 000 peut aider les élèves au cycle primaire à mieux comprendre les nombres en permettant de les comparer et de faire ressortir les relations entre eux.
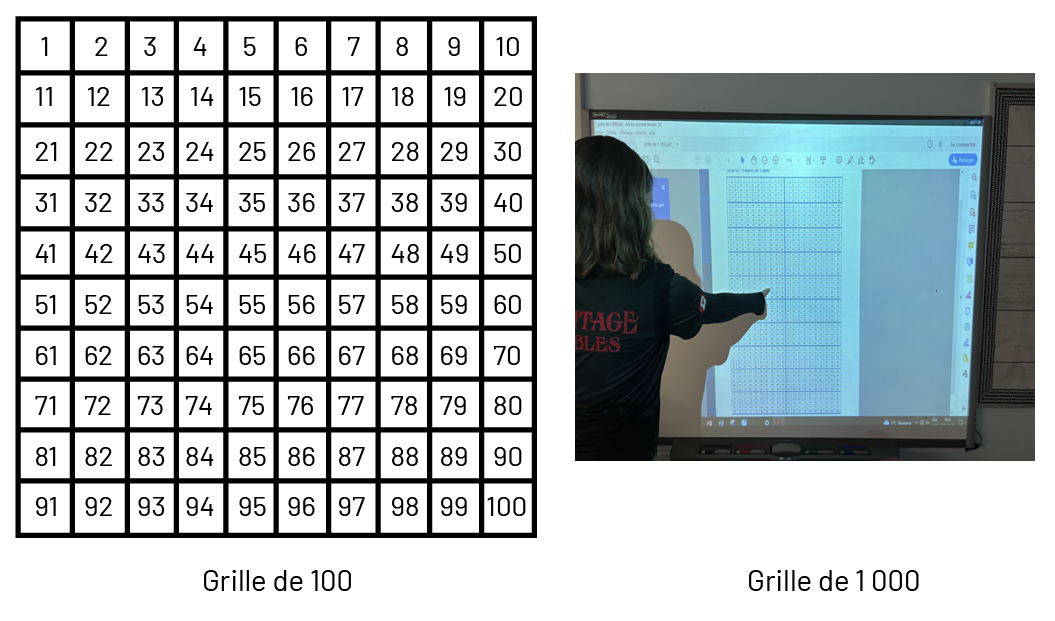
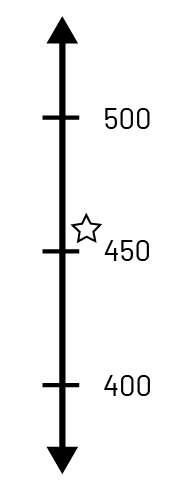
Droite numérique : Au cycle primaire, les élèves utilisent et construisent des droites numériques pour compter par intervalles ou pour identifier le nombre de dizaines dans un nombre. L’utilisation et la construction de droites numériques variées permettent aux élèves de représenter de grands nombres et de reconnaître les relations entre eux. Voici quelques exemples de droites numériques sur lesquelles le nombre 457 est représenté :
- droite numérique dont l’échelle est par intervalles de 250;
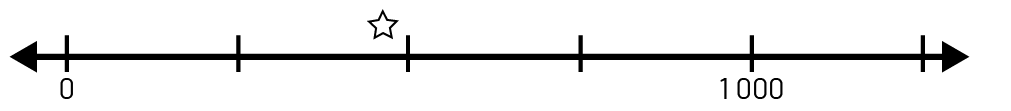
- droite numérique qui ne commence pas à 0, dont l’échelle est par intervalles de 20;
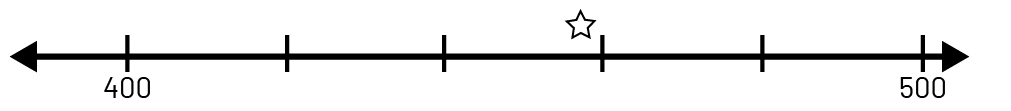
- droite numérique ouverte (qui n’est pas graduée) sur laquelle les nombres sont placés en relation les uns avec les autres;
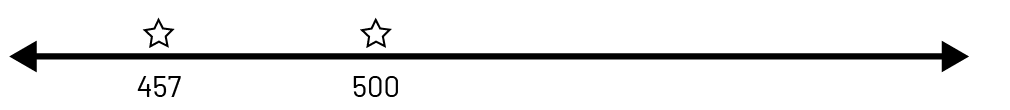
- droite numérique verticale qui présente les nombres en ordre croissant vers le haut et qui fait des liens avec les autres domaines dont Sens de l’espace (par exemple, thermomètre) et Données (par exemple, axe des ordonnées).
Représentations symboliques
Les nombres sont représentés symboliquement à l’aide des chiffres qui les composent.
L’écriture des grands nombres nécessite une bonne maîtrise du concept de valeur de position, faute de quoi l’élève à qui l’on demande d’écrire symboliquement « 513 » pourrait écrire 500 13. Elle nécessite aussi une compréhension du rôle du 0 pour indiquer l’absence d’une quantité dans une des positions.
Un nombre peut être représenté de différentes façons à l’aide de symboles mathématiques, soit en respectant la valeur de la position de chaque chiffre (836 est égal à \(800 + 30 + 6\)), soit d’après quelques valeurs de position (836 est égal à 83 dizaines et 6 unités) ou encore en effectuant différentes opérations (836 est égal à \(800 + 36\) ou \(840 - 4\) ou \(800 + 10 + 10 + 10 + 6\)). En fait, il existe une infinité de façons de représenter un nombre, chacune permettant aux élèves de se donner une autre façon de l’interpréter et d’en comprendre le sens.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 64-71.
Habileté : composer et décomposer les nombres naturels
La décomposition et le regroupement sont des notions réciproques liées aux concepts de quantités finales, initiales, ajoutées ou unies. La décomposition implique qu’une quantité finale peut être décomposée en différentes quantités initiales, ajoutées, unies ou comparées. Alors que le regroupement implique que différentes quantités initiales, unies ou ajoutées peuvent être regroupées pour former une quantité finale.
En 3e année, les élèves acquièrent une compréhension du concept de la quantité et de la structure des nombres en base 10. Ils sont alors en mesure de comprendre qu’un nombre peut être décomposé en fonction des valeurs de position (par exemple, 425 peut être décomposé en 4 centaines, 2 dizaines et 5 unités) et que, de façon réciproque, il est possible de regrouper les éléments d’un ensemble en dizaines ou en centaines afin de déterminer le nombre d’éléments (par exemple, regrouper les éléments d’un ensemble en 4 centaines, 2 dizaines et 5 unités et conclure que l’ensemble contient 425 éléments).
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 47.
Il importe donc de proposer aux élèves de nombreuses activités consistant à décomposer des nombres en dizaines et en unités afin de les aider à saisir le concept de la quantité reliée à la valeur de position.
Habileté : décrire les façons dont les nombres sont utilisés dans la vie quotidienne
Pour comprendre le concept d’un nombre, il faut établir des liens entre le symbole (par exemple, 684), le mot (par exemple, six cent quatre-vingt-quatre), la quantité (par exemple, 684 objets) ou le rang (par exemple, le 684e banc dans une salle de spectacle). Les nombres sont aussi parfois utilisés comme simple code, sans référence à une quantité ou à un rang (par exemple, 4 dans un numéro de téléphone ou sur un maillot de soccer). Les adultes, qui ont depuis longtemps compris que le sens des nombres dépend du contexte dans lequel ils sont utilisés, n’ont souvent pas conscience de la difficulté que peuvent avoir les enfants à saisir ces différences.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 73.
Connaissance : nombres naturels
Les nombres naturels appartiennent à l’ensemble N = {0, 1, 2, 3, 4, 5, 6, 7, 8,…}.
