B1.7 Représenter et résoudre des problèmes de partage équitable ciblant la recherche et l’utilisation des fractions équivalentes, y compris des problèmes comportant des demis, des quarts et des huitièmes; des tiers et des sixièmes; ou des cinquièmes et des dixièmes.
Habileté : cibler la recherche et l’utilisation de fractions équivalentes dans la résolution de problèmes de partage équitable
La notion de fractions équivalentes est abordée dès la 1re année. Toutefois, il est parfois difficile pour les élèves de saisir qu’une quantité peut porter plusieurs noms et être représentée par plusieurs nombres (par exemple, le nombre \(1 \frac{2}{3}\) représente la même quantité que le nombre \(1 \frac{4}{6}\); donc, on peut affirmer que \(1 \frac{2}{3} = 1 \frac{4}{6}\)).
La compréhension des fractions équivalentes fait partie du raisonnement proportionnel que les élèves vont continuer à développer aux cycles moyen et intermédiaire.
Déterminer des fractions équivalentes, c’est déterminer des fractions qui représentent la même quantité. On cherche alors un nombre de « petites parties » d’un tout qui correspondent à un nombre particulier de « grandes parties » du même tout. Par exemple, si on cherche le nombre de huitièmes qui correspond à un quart (\(\frac{1}{4} = \frac{\mathord{?}}{8}\)) :
\(\frac{1}{4}\) d’une tablette de chocolat
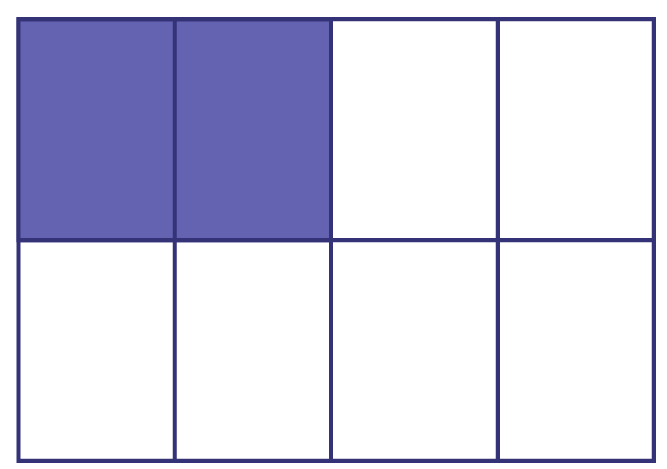
\(\frac{2}{8}\) de la même tablette de chocolat
La relation d’équivalence doit aussi être explorée par rapport aux fractions d’un ensemble. Dans l’image ci-dessous, les élèves voient aisément que \(\frac{6}{10}\) des bonbons sont emballés dans des papillotes mauves.
Toutefois, ils ont de la difficulté à déterminer d’autres fractions équivalentes. Il importe alors de présenter des activités qui leur permettent de manipuler les éléments de l’ensemble. Ainsi, les élèves peuvent les grouper en ensembles de 2 et déterminer des fractions équivalentes.
\(\frac{3}{5}\) des bonbons sont emballés dans des papillotes mauves
L’expérience concrète avec les fractions équivalentes est le fondement du raisonnement proportionnel. On ne saurait lui accorder trop d’importance. C’est pourquoi le personnel enseignant doit planifier des activités qui reposent sur les notions informelles reliées aux fractions équivalentes.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 50-53.
Des modèles et des outils peuvent être utilisés pour développer la compréhension des fractions équivalentes.
Exemples
- Des bandes de fractions ou d’autres modèles, comme des cercles fractionnaires, peuvent créer la même aire que la fraction d’origine lorsqu’on utilise des parties fractionnées ou assemblées.
- Des bandes de papier peuvent être pliées pour montrer le fractionnement afin de créer des parties équivalentes.
- Une droite numérique double peut être utilisée pour représenter des fractions équivalentes basées sur différentes échelles.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Habileté : représenter des fractions dans divers contextes
Le contexte est constitué de l’ensemble des renseignements entourant une situation. Dans l’étude des fractions, le tout est une partie essentielle du contexte. En effet, une fraction comme \(\frac{2}{3}\), sans mention du tout, n’offre pas suffisamment d’information pour que la quantité correspondant à la fraction en contexte soit bien cernée. Par exemple, quand il est question de \(\frac{1}{2}\), les gens conçoivent généralement que c’est peu. Pourtant, il faut considérer cette quantité en contexte — comme on le fait pour les nombres naturels — puisqu’on peut porter divers jugements sur une même fraction. Manger la moitié d’une pomme à la collation, c’est peu; manger la moitié d’une tarte, c’est beaucoup; si la moitié des élèves de la classe sont absents, c’est beaucoup. Le contexte est donc essentiel si on veut porter un jugement éclairé sur la quantité représentée par une fraction. Il est aussi important que les élèves apprennent à toujours tenir compte du tout. Une fraction n’a aucun sens si elle n’est pas mise en relation avec un tout. Par exemple, on ne peut comparer une demi-pizza et un tiers de pizza si elles n’ont pas la même superficie à moins que l’on nous présente les pizzas en question. Le personnel enseignant doit présenter des situations d’apprentissage qui permettent aux élèves de découvrir qu’une fraction ne révèle rien de la taille du tout ou de ses parties; elle nous renseigne seulement sur la relation qui existe entre un tout et ses parties.
Dans toute situation, le tout correspond à un élément ou à un ensemble d’éléments.
Si le tout correspond à un élément, on peut le fractionner en parties équivalentes. Chacune des parties peut alors être comparée au tout.
Exemples
Image Le tout est un objet : Un pamplemousse, puis un demi-pamplemousse. Le tout est une surface : Un hexagone. Une partie de l’hexagone est en vert, cela représente un sixième de la surface de l’hexagone. Le tout est une longueur : Un segment tracé en noir. Le segment est divisé en 3 parties égales, 2 d’entre elles sont rouges. Cela représente 2 tiers du segment.
Si le tout correspond à un ensemble d’éléments, soit une collection d’objets, quelques-uns des éléments peuvent être regroupés pour former une partie de l’ensemble et représenter ainsi une partie du tout.
Exemples
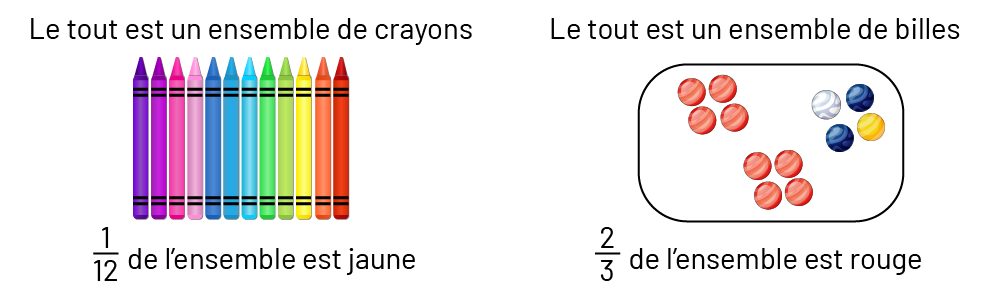Image Le tout est un ensemble de crayons :!2 crayons multicolores. Un douzième de l’ensemble est jaune.Le tout est un ensemble de billes :Dans un encadré, il y a 8 billes rouges, 2 billes bleues, une bille blanche et une bille jaune.2 tiers de l’ensemble est rouges.
En général, lorsqu’il est question de fractions, on se réfère à 3 modèles de tout : le modèle d’ensemble, le modèle de longueur et le modèle de surface.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 31-32.
Connaissance : fractions équivalentes
Différentes fractions peuvent représenter la même quantité. \(\frac{5}{10}\), \(\frac{4}{8}\), \(\frac{3}{6}\) et \(\frac{2}{4}\) représentent tous la même quantité, soit un demi du même tout. On considère que les fractions sont équivalentes lorsqu’elles représentent le même nombre ou la même quantité.
Lorsque 2 fractions sont équivalentes, les relations entre le numérateur et le dénominateur sont constantes. Par exemple, dans \(\frac{1}{2}\) et \(\frac{2}{4}\), le dénominateur dans les 2 fractions correspond au double du numérateur, et le numérateur d’une fraction correspond au double de l’autre, tout comme le dénominateur de l’une correspond au double de l’autre.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.