B2.1 Utiliser les propriétés des opérations, et démontrer les relations entre la multiplication et la division pour résoudre des problèmes et vérifier la vraisemblance des calculs.
Habileté : utiliser les propriétés des opérations pour résoudre des problèmes et vérifier la vraisemblance des calculs
Les élèves démontrent leur compréhension des propriétés des opérations mathématiques avec des objets ou des nombres spécifiques. Les élèves utilisent du matériel concret, des dessins, des mots ou des symboles pour représenter des idées mathématiques et des relations.
Il n’est pas nécessaire que les élèves du primaire connaissent le nom des propriétés. Il suffit qu’elles et ils les utilisent naturellement pour combiner des nombres.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 33.
La commutativité
L’addition et la multiplication sont commutatives. Par exemple, on peut démontrer la commutativité de l’addition comme suit :
Image Un segment, fléché à ses extrémités, est divisé en 6 parties égales. Au-dessus du segment,
un rectangle rouge
représente 2 parties, et un rectangle bleu représente 3 parties. La phrase mathématique est : 2 plus 3. En dessous du
segment, un rectangle bleu représente 3 parties et un rectangle rouge représente 2 parties. La phrase
mathématique est : 3 plus 2
On reconnaît alors que si les termes d’une addition sont intervertis, le résultat demeure le même.
On peut aussi démontrer la commutativité de la multiplication. Par exemple, \(8 \times 3\) et \(3 \times 8\).
Image Disposition rectangulaire qui représente la phrase mathématique : 8 multiplié par 3 égal 24.
8 rangées de 3 cœurs. Disposition rectangulaire qui représente la phrase mathématique : 3 multiplié par 8 égal 24. 3
rangées de 8 cœurs.
Les 2 dispositions précédentes représentent la même quantité totale, organisée de 2 façons différentes. De ce fait, elles illustrent 2 situations différentes. Ainsi, \(8 \times 3\) représente 8 rangées de 3 objets, tandis que \(3 \times 8\) représente 3 rangées de 8 objets. Il est important que les élèves reconnaissent les différentes représentations.
On peut aussi utiliser un exemple du quotidien. Par exemple, le personnel enseignant invite 3 élèves qui ont exactement 1 frère ou 1 sœur à venir représenter au tableau le nombre d’enfants dans leur famille. Le nombre total d’enfants est représenté par \(3 \times 2\) enfants, pour un total de 6 enfants (Figure 1).
Ensuite, le personnel enseignant fait la même démarche avec 2 enfants qui ont exactement 2 frères ou sœurs. Le nombre total d’enfants est représenté par \(2 \times 3\) enfants, pour un total de 6 enfants (Figure 2).
Figure 1
Figure 2
Les 2 phrases mathématiques, \(3 \times 2 = 6\) et \(2 \times 3 = 6\), indiquent un même résultat, même si l’ordre des facteurs est inversé. Les élèves peuvent alors comprendre que 3 familles de 2 enfants ou 2 familles de 3 enfants donnent un total de 6 enfants, sans que les situations soient identiques.
Au début de l’apprentissage de la multiplication, les élèves perçoivent souvent la multiplication comme une addition répétée. En tentant de résoudre une variété de problèmes, ils peuvent utiliser la commutativité de la multiplication pour développer une stratégie plus efficace de calcul.
Par exemple, les élèves qui utilisent l’addition répétée reconnaîtraient que \(2 \times 12 \ (12 + 12)\) est plus simple et moins long à représenter et à calculer que \(12 \times 2 \ (2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2)\).
Une disposition rectangulaire est un excellent modèle visuel pour représenter la commutativité de la multiplication.
Image 3 élèves observe une grille, chaque élève a une différente perspective de la grille. L’élève
un dit : « Moi, je vois plutôt 3 rangées de 5, donc 3 multipliés par 5. » L’élève 2 dit : « JE vois 5 rangées de 3,
donc 5 multipliés par 3. » L’élève 3 dit : « Je vois 5 colonnes de 3 rangées qui peuvent aussi être représentées par 5
multipliées par 3.
Associativité
L’associativité de la multiplication (par exemple, \(3 \times 2 \times 5 = 3 \times (2 \times 5)\) ou \(3 \times 2 \times 5 = (3 \times 2) \times 5\) n’est pas facile à comprendre. Certes, on peut la constater en vérifiant les résultats des multiplications, mais cela ne constitue pas une compréhension. Pour comprendre, on peut utiliser un prolongement du modèle d’une disposition rectangulaire à l’aide de cubes.
Dans la figure 1, on voit qu’il y a 2 rangées de 5 cubes, soit \(2 \times 5\) cubes. Dans la figure 2, on voit 3 étages contenant chacun \(2 \times 5\) cubes. La figure représente donc \(3 \times (2 \times 5)\) cubes.
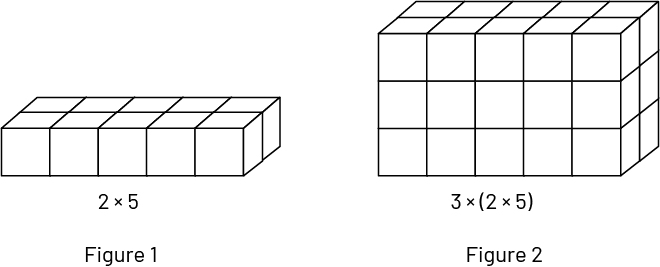Image Figure un : Figure de 2 rangées de 5 cubes. La phrase mathématique est : 2 multiplié par 5.
Figure 2 3 étages, de 2 rangées de 5 cubes. La phrase mathématique est : 3 multiplié par (parenthèse ouvrante) 2
multiplié par 5 (parenthèse fermante).
On peut aussi considérer la figure 3, qui illustre 3 étages de 2 cubes, soit \(3 \times 2\) cubes. La figure 4 peut alors représenter \(3 \times 2\) cubes qui paraissent 5 fois, soit \((3 \times 2) \times 5\).
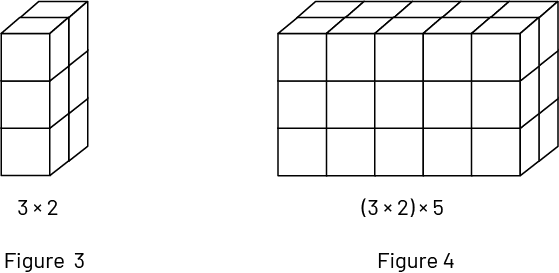Image Figure un : 3 rangées de 2 cubes. La phrase mathématique est : 3 multiplié par 2. Figure 2 :
3 étages de 2 rangées de 5 cubes. La phrase mathématique est : (Parenthèse ouvrante) 3 multiplié par 2 (parenthèse
fermante) multiplié par 5.
On voit donc que \(3 \times (2 \times 5)\) et \((3 \times 2) \times 5\) représentent la même quantité de cubes (même si chaque expression représente un point de vue différent) et que chacune donne le même produit que \(3 \times 2 \times 5\).
Devant une expression numérique telle que \(3 \times (2 \times 5) = \mathord{?}\), certains élèves tentent parfois d’appliquer la distributivité de manière à calculer \((3 \times 2) \times (3 \times 5)\), ce qui a pour effet que \(2 \times 5\) est multiplié par 9, plutôt que par 3. Dans un tel cas, il faut rappeler que la distributivité de la multiplication s’effectue seulement sur l’addition ou la soustraction et expliquer la situation en utilisant un modèle concret ou semi-concret.
L’associativité ne change pas l’ordre des nombres d’une expression numérique. On peut cependant jumeler l’associativité et la commutativité pour faciliter l’évaluation d’une expression numérique.
Par exemple, pour déterminer la valeur de l’expression \(2 \times 3 \times 5\), on peut déterminer celle de l’expression \((2 \times 5) \times 3\). En effet, il est habituellement plus facile de calculer \(10 \times 3\) que de calculer \(6 \times 5\).
La distributivité
L’exemple suivant illustre comment on peut utiliser la distributivité pour calculer \(6 \times 8\). Dans un cas, on décompose le facteur 8 pour obtenir \(5 + 3\). On a alors \(6 \times (5 + 3) = (6 \times 5) + (6 \times 3)\). Dans l’autre cas, on décompose le facteur 6 pour obtenir \(3 + 3\). On a alors \((3 + 3) \times 8 = (3 \times 8) + (3 \times 8)\).
Image Disposition rectangulaire qui représente la phrase mathématique : 6 multiplié par 8. 6
rangées de 8 triangles. Disposition rectangulaire qui représente la phrase mathématique : (parenthèse ouvrante) 6
multiplié par 5 (parenthèse
fermante) plus (parenthèse ouvrante) 6 multiplié par 3 (parenthèse fermante). 6 rangées de 5 triangles. Et 6 rangées
de 3 triangles. Disposition rectangulaire qui représente la phrase mathématique : (parenthèse ouvrante) 3 multiplié
par 8 (parenthèse
fermante) plus (parenthèse ouvrante) 3 multiplié par 8 (parenthèse fermante). 3 rangées de 8 triangles, et 3 rangées
de 8 triangles.
Seule la multiplication est distributive. On pourrait reconnaître que la division est partiellement distributive. Par exemple, pour calculer \(32 \div 8\), il est possible de décomposer le dividende 32 pour obtenir \(16 + 16\). On a alors \((16 + 16) \div 8\) et la division par 8 est distribuée sur l’addition. On obtient \((16 \div 8) + (16 \div 8) = 2 + 2\), soit 4. Cependant si le diviseur est décomposé, la distributivité ne fonctionne pas. Par exemple, \(32 \div 8 \neq (32 \div 4) + (32 \div 4)\). C’est la raison pour laquelle la distributivité n’est pas une propriété de la division.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 102-106.
Une propriété peut être utilisée pour vérifier une réponse. Par exemple, \(4 \times 9\) peut d’abord être déterminé en utilisant la distributivité, \(2 \times 9 + 2 \times 9\) ou en décomposant \(4 \times 9\) en \(2 \times 2 \times 9\) et en utilisant l’associativité, \(2 \times (2 \times 9)\).
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Habileté : utiliser les relations entre la multiplication et la division pour résoudre des problèmes
Comprendre les relations entre les opérations permet de les utiliser avec plus de souplesse.
Plus les élèves ont l’occasion de manier les opérations, plus elles et ils peuvent remarquer et comprendre les liens entre elles. Les élèves peuvent même utiliser des stratégies d’addition ou de soustraction pour résoudre des multiplications et des divisions.
Au cycle primaire, les élèves ont établi des liens entre les opérations à travers diverses activités. Par exemple, les élèves savent que l’addition et la soustraction sont des opérations inverses et que l’addition est commutative. Avec le temps, ils développent leur sens du nombre et leur sens des opérations et s’en servent graduellement avant d’effectuer des opérations. Cette pratique, quoique souvent informelle et mentale, demeure toutefois essentielle à la compréhension des relations entre les nombres et entre les opérations.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 97.
La multiplication et la division
La multiplication et la division sont des opérations inverses. On peut également les relier au concept de tout et de ses parties. Dans la multiplication, on regroupe les parties qui sont des groupes égaux, alors que dans la division, on décompose un tout en groupes égaux. À partir de cette relation entre la multiplication et la division, les élèves peuvent utiliser les faits numériques relatifs à la multiplication pour effectuer une division. Il arrive souvent que les élèves saisissent mal la relation d’opération inverse entre la multiplication et la division, même après avoir effectué des divisions et vérifié leurs calculs. Il est donc essentiel de revenir régulièrement sur le sens de chacune des opérations en contexte de résolution de problèmes.
Pour comprendre la multiplication et la division, il faut reconnaître les 3 types de quantités qui entrent en jeu, soit la quantité totale (par exemple, 8 fleurs), le nombre de groupes égaux (par exemple, 4 pots) et la taille de chaque groupe (par exemple, 2 fleurs par pot).
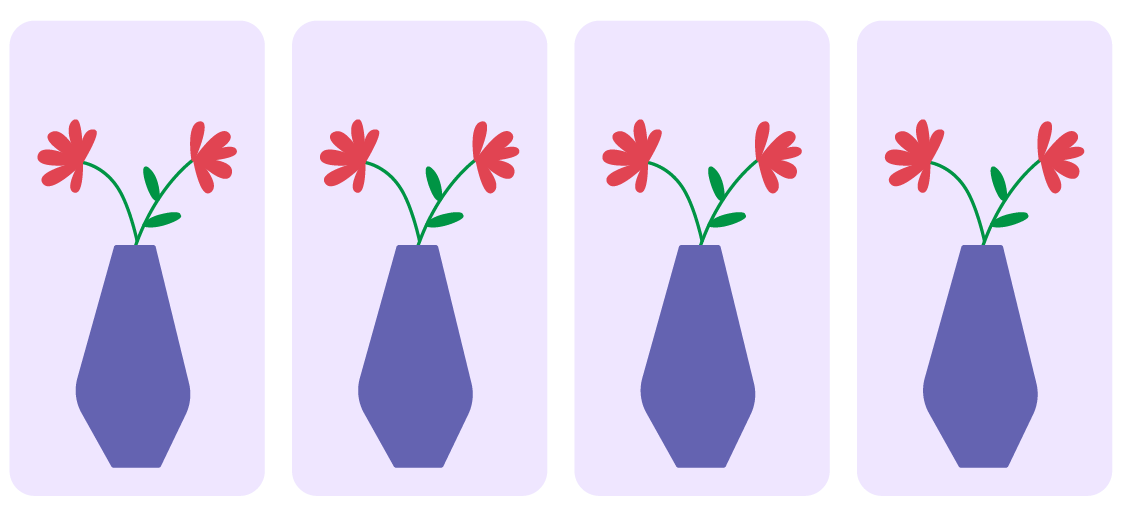
Dans les problèmes présentés aux élèves, on associe trop souvent la division à un seul sens, soit le partage. Le sens de groupement est habituellement négligé. La division a un sens de partage lorsque la quantité totale et le nombre de groupes sont connus (par exemple, 3 élèves veulent se partager équitablement 15 pommes et on cherche le nombre de pommes que chacun recevra).
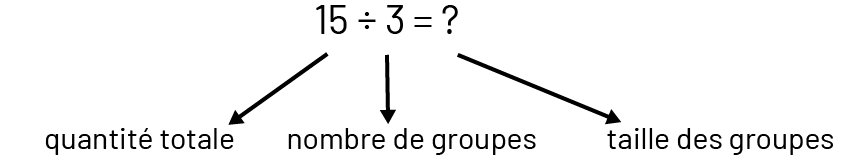
La division a un sens de groupement lorsque la quantité totale et le nombre d’éléments dans chaque groupe (taille des groupes) sont connus (par exemple, on a 15 pommes et on veut les placer dans des sacs, 3 pommes par sac; on cherche le nombre de sacs qu’il faut).
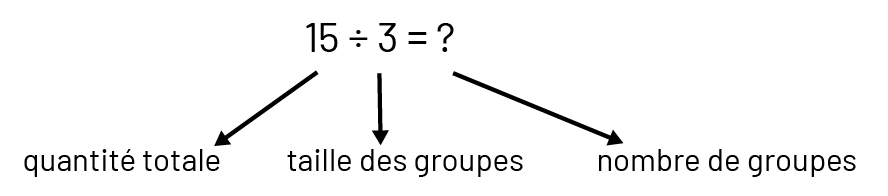
Il est essentiel de traiter des 2 types de problèmes, puisqu’ils sont la base de l’intégration d’autres concepts mathématiques. Il n’est pas nécessaire que les élèves sachent le nom des types de problèmes, mais il est essentiel qu’elles et ils aient l’occasion d’en résoudre de divers types, tout en employant une variété de stratégies.
Image Tableau de types de problème et de quantités inconnues. Problème de groupes égaux : Produit
inconnu : Nombre multiplié par nombre égal inconnu. Exemple : « Julie a acheté 5 livres pour ses camarades. Chaque
livre a couté 2 dollars. Combien a-t-elle dépensé pour
tous ces livres? 5 multiplié par 2 égal inconnue. Taille des groupes inconnue, (parenthèse ouvrante) sens de partage
(parenthèse fermante) Nombre divisée par nombre égal inconnue. Exemple : « Julie a dix livres. Elle veut les donner à
5 de ses camarades de manière que chacun en reçoive le même
nombre. Combien de livres recevra chaque camarade? Dix divisé par 5 égal inconnue. Nombre de groupe inconnu.
(Parenthèse ouvrante) sens de groupement (parenthèse fermante). Nombre divisé par nombre égal inconnu. Exemple : «
Julie a acheté dix livres pour ses camarades et prépare ses sacs cadeaux. Elle met 2 livres dans chaque
sac. Combien de sacs-cadeaux Julie a-t-elle utilisés? Dix divisé par 2 égal inconnu.
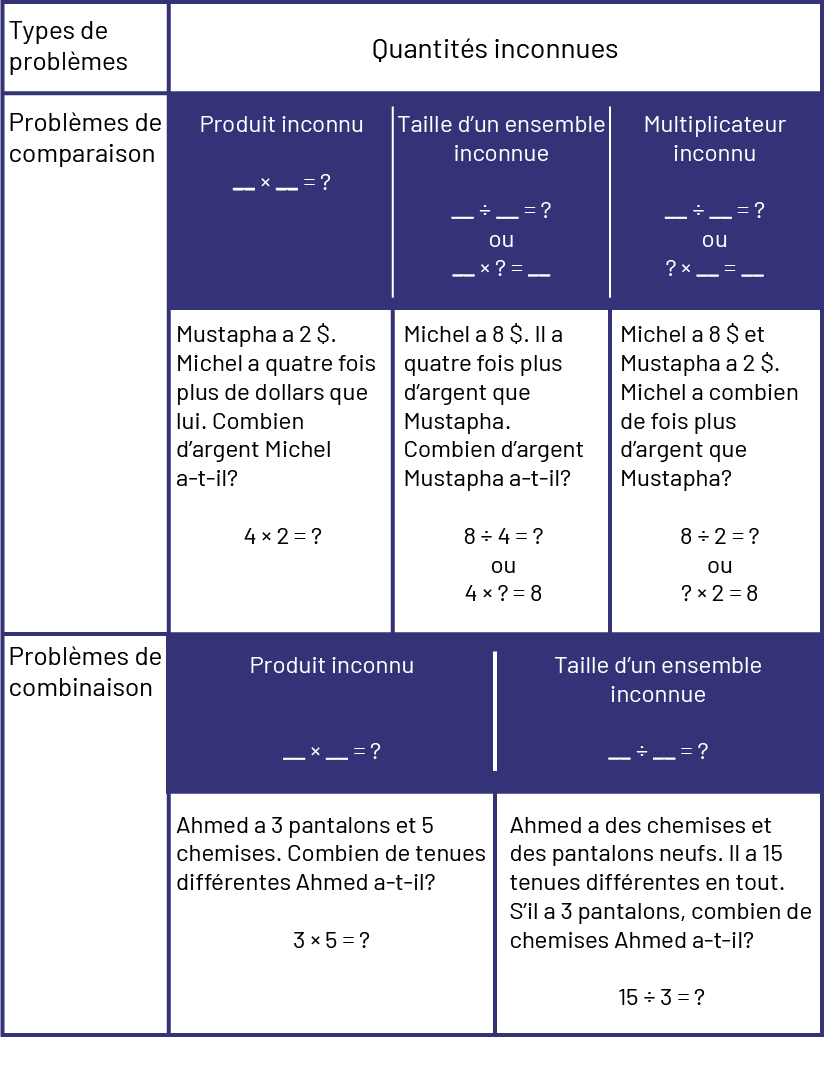Image Tableau de types de problème et de quantités inconnues. Problèmes de comparaison. Produit
inconnu : nombre
multiplié par nombre égal inconnue. Exemple:« Mustapha 2 dollars. Michel a 4 fois plus de dollars que lui. Combien
d’argent Michel a-t-il? » 4 multiplié par 2 égal inconnue. Taille des groupes inconnue, nombre divisée par nombre égal
inconnue ou nombre multiplié par inconnue égal nombre. Exemple: « Michel a 8 dollars. Il a quatre fois plus d’argent
que Mustapha. Combien d’argent Mustapha a-t-il? » 8 divisé par 4 égal inconnue. Ou 4 multiplié par inconnue égal 8.
Multiplicateur inconnu. Nombre divisé par nombre égale inconnue. Ou Inconnue multipliée par nombre égal nombre.
Exemple : « Michel a 8 dollars et Mustapha a 2 dollars. Michel a combine de fois plus d’argent que Mustapha? » 8
divisé par 2 égal inconnue. Ou Inconnue multipliée par 2 égal 8. Problèmes de combinaison. Produit inconnu. Nombre
multiplié par nombre égal inconnue. Exemple : Ahmed a 3 pantalons et 5 chemises. Combien de tenues différentes Ahmed
a-t-il? 3 multiplié par 5 égal inconnue. Taille d’un ensemble inconnue. Nombre divisé par nombre égal inconnue.
Exemple : Ahmed a des chemises et des pantalons neufs. Il a 15 tenues différentes en tout. S’il a 3 pantalons,
combien de chemises Ahmed a-t-il? 15 divisé par 3 égal inconnue.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 84-86.
Connaissance : propriété des opérations
Les propriétés des opérations sont des caractéristiques qui sont propres aux opérations, peu importe les nombres en cause.
Les propriétés des opérations sont :
- La commutativité : \((3 + 5 = 5 + 3)\);
- L’associativité : \((2 + 9) + 11 = 2 + (9 + 11)\);
- La distributivité : \(8 \times 7 = (8 \times 5) + (8 \times 2)\);
- L’élément neutre : \(13 + 0 = 13\), \(0 + 13 = 13\); \(25 \times 1 = 25\), \(1 \times 25 = 25\)
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 102.
Connaissance : la commutativité
Une opération est commutative si son résultat demeure inchangé lorsqu’on intervertit l’ordre des termes qui la composent. L’addition et la multiplication sont commutatives. Par exemple, \(7 + 33 = 33 + 7\) et \(2 \times 3 = 3 \times 2\).
Connaissance : l’associativité
L’associativité est une propriété de l’addition et de la multiplication. Elle permet de combiner les termes d’une expression de différentes façons sans en modifier la valeur.
Connaissance : élément neutre
Comme son nom l’indique, un élément neutre est un nombre qui n’a aucun effet pour une opération donnée. Ainsi, le nombre 0 est l’élément neutre de l’addition (par exemple, \(287 + 0 = 287\) et \(0 + 287 = 287\)) et le nombre 1 est l’élément neutre de la multiplication (par exemple, \(133 \times 1 = 133\) et \(1 \times 133 = 133\)).
La soustraction et la division n’ont pas d’élément neutre. Dans une soustraction, le nombre 0 ne produit aucun effet lorsqu’il est le 2e terme (par exemple, \(3 - 0 = 3\) ), mais ce n’est pas le cas s’il paraît comme 1er terme (par exemple, \(0 - 3 \neq 3\)). Ainsi, le nombre 0 n’est pas neutre pour la soustraction. De même, dans une division, le nombre 1 ne produit aucun effet lorsqu’il est le diviseur (par exemple, \(3 \div 1 = 3\)), mais ce n’est pas le cas s’il paraît comme dividende (par exemple, \(1 \div 3 \neq 3\)). Ainsi, le nombre 1 n’est pas neutre pour la division.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 107.
Connaissance : relations entre l’addition, la soustraction, la multiplication et la division
- L’addition et la soustraction sont des opérations inverses.
- La multiplication peut être associée à une addition répétée.
- La division peut être associée à une soustraction répétée.
- La multiplication et la division sont des opérations inverses.