B2.4 Démontrer sa compréhension des algorithmes de l’addition et de la soustraction de nombres naturels en établissant des liens avec les outils et les stratégies utilisés pour additionner et soustraire, et décrire ces liens.
Habileté : démontrer sa compréhension des algorithmes de l’addition et de la soustraction
Les algorithmes sont des ensembles de règles et d’actions ordonnées nécessaires à la résolution d’une addition, d’une soustraction, d’une multiplication ou d’une division. En termes simples, un algorithme est la « recette » d’une opération (Kilpatrick, Swafford et Findell, 2001, p. 103).
Pour favoriser la maîtrise des opérations arithmétiques, il importe de mettre l’accent sur l’efficacité et la souplesse avec lesquelles il faut utiliser les algorithmes. Les élèves qui abordent les nombres avec souplesse sont plus susceptibles d’utiliser des stratégies efficientes, de travailler avec précision et d’acquérir de solides fondements pour comprendre d’autres algorithmes usuels. Les études ont abondamment démontré qu’il est très utile pour les élèves d’avoir de nombreuses occasions d’élaborer leurs propres stratégies sur les nombres à plusieurs chiffres (Morrow et Kenney, 1998).
Par le passé, plusieurs personnes présumaient qu’il n’y avait qu’une façon d’effectuer l’opération, soit l’algorithme appris. Les différences culturelles sur la façon dont de telles opérations sont effectuées indiquent toutefois qu’un algorithme usuel peut avoir de nombreuses variantes. Les adultes ont tendance à penser que l’algorithme qu’on leur a enseigné est le seul possible. En réalité, il y a différentes façons d’utiliser un algorithme « usuel ». L’encadré qui suit donne quelques exemples des différentes façons de résoudre \(27 + 48\) à l’aide de variantes de l’algorithme « usuel ».
Chaque algorithme « usuel » présente un niveau différent d’abstraction. Ils servent ici à montrer les différences dans la façon d’utiliser un algorithme. Certaines étapes sont plus explicites que d’autres ou sont raccourcies pour créer une façon plus rapide, mais plus abstraite d’arriver à la réponse.
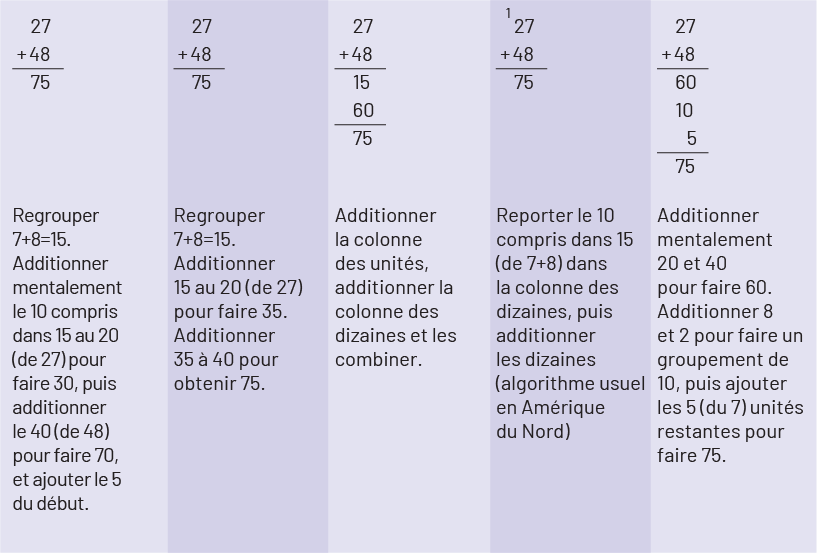
Image Addition verticale : 27 plus 48 égal 75.Regrouper 7 plus 8 égal 15. Additionner mentalement le dix dans le 15 au 20 « de 27 » pour faire 30, puis additionner le 40« de 48 » pour faire 70, et ajouter le 5 du début. Addition verticale : 27 plus 48 égal 75. Regrouper 7 plus 8 égal 15. Additionner 15 et 20 « de 27 » pour faire 35. Additionner 35 et 40 pour obtenir 75. Addition verticale : 27 plus 48 égal 15 plus 60 égal 75. Additionner la colonne des unités, additionner la colonne des dizaines et les combiner. Addition verticale : 27 plus 48 égal 75, la retenue un est au-dessus du 2 de 27. Reporter le dix compris dans le 15 « de 7 plus 8 », dans la colonne des dizaines, puis additionner les dizaines « algorithme usuel en Amérique du nord ». Addition verticale : 27 plus 48 égal 60 plus dix plus 5 égal 75. Additionner mentalement 20 et 40 pour faire 60. Additionner 8 et 2 pour faire un groupement de dix, puis ajouter les 5 « du 7 » unités restantes pour faire 75.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 34-36.
Enseignement des algorithmes
Il est très important que les élèves aient de nombreuses occasions de la maternelle à la 3e année de développer les habiletés nécessaires pour effectuer des calculs en utilisant les concepts de réunion, les points d’ancrage 5 et 10 et les faits numériques de base jusqu’à 20. L’expérience que les élèves acquièrent de la décomposition des nombres en unités, en dizaines et parfois en centaines au cours de leurs premières années d’études les aidera à faire le lien entre ces concepts fondamentaux et les opérations sur les nombres à plusieurs chiffres.
Le recours aux illustrations, au langage (parlé et écrit) et aux nombres pour communiquer leurs calculs aide les élèves à établir des liens entre les niveaux concret, visuel et abstrait de leur compréhension des opérations sur les nombres. La présentation prématurée de symboles abstraits (par exemple, le signe =) sans relier de tels symboles aux concepts qu’ils représentent (par exemple, le signe = représente l’équivalence ou l’équilibre) est souvent la source des difficultés qu’éprouvent les élèves en calcul. Plutôt que de rechercher le sens de l’opération, ils commencent à percevoir les mathématiques comme une série de règles et de procédures routinières peu applicables à la résolution des problèmes de tous les jours. Les expériences que les élèves font doivent leur permettre de dégager le sens des algorithmes et de développer des stratégies efficientes qui peuvent être généralisables.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 39.
Algorithmes créés par les élèves
En salle de classe, il est suggéré d’examiner plusieurs algorithmes pour une même opération. Il est essentiel que les élèves comprennent le raisonnement derrière les gestes posés dans ces algorithmes. Avec le temps, cela leur permet de choisir une stratégie efficace selon le contexte. Le personnel enseignant qui a dans sa classe des élèves de cultures différentes peut les inviter à discuter, à la maison, de la méthode que les parents utilisent pour effectuer une addition ou une soustraction. Ces élèves peuvent présenter ces méthodes à la classe, ce qui peut apporter de nouvelles stratégies.
On présente souvent les algorithmes usuels comme principale stratégie de calcul. Bien qu’ils soient efficaces, ils ne sont pas toujours appropriés. Lorsque l’enseignement est axé sur l’algorithme usuel, par exemple, pour calculer \(300 - 15\), les élèves ont tendance à sortir un crayon et à résoudre le problème par écrit, avec l’algorithme écrit et ses échanges, ce qui est une source commune d’erreurs. Il est pourtant plus efficace de calculer mentalement comme suit : \(300 - 10 = 290, \ 290 - 5 = 285\). De plus, l’algorithme usuel n’est pas la meilleure méthode à utiliser là où une estimation suffit. C’est pourquoi il est suggéré de considérer l’algorithme usuel comme une stratégie de calcul parmi tant d’autres.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 119.
Les élèves peuvent résoudre des problèmes écrits de différentes façons. Voici des exemples d’algorithmes d’addition et de soustraction. Ce ne sont pas les seules façons de résoudre un problème, il en existe beaucoup d’autres, aussi faut-il donner aux élèves des occasions de raisonner pour découvrir d’autres façons de faire.
Exemples d’algorithmes d’addition
\(566 + 379\)
L’élève procède par étapes et décompose le dernier nombre seulement.
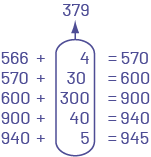
Image Des additions sont superposées : 566 plus 4 égal 570. 570 plus 30 égal 600. 600 plus 300 égal 900. 900 plus 40 égal 940. 940 plus 5 égal 945. Tous les deuxième nombre des additions sont encerclés, et additionnés pour un total de 379.
L’élève décompose horizontalement les nombres.
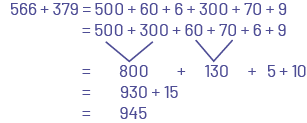
Image 566 plus 379 égal 500 plus 60, plus 6 plus, 300 plus, 70 plus, 9. Égal 500 plus 300, plus 60 plus 70 plus 6, plus 9. Égal 800 plus 130 plus, 5 plus 10. Égal 930 plus 15. Égal 945.
L’élève regroupe les centaines, les dizaines et les unités.
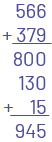
L’élève utilise une technique de compensation.
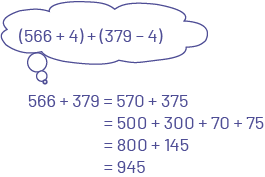
Image Dans une bulle de pensée on peut lire : (Parenthèse ouvrante) 566 plus 4 (parenthèse fermante) plus (parenthèse ouvrante) 370 moins 4 (parenthèse fermante). 566 plus 379 égal 570 plus 375 Égal 500 plus 300, plus 70 plus 75. Égal 800 plus 145. Égal 945.
Source : Les mathématiques… un peu, beaucoup, à la folie!, Guide pédagogique, Édition révisée, Numération et sens du nombre, 3e année, Module 3, Série 2, Activité 2 - Les clients de l’usine Aux mille délices, p. 432.
Exemples d’algorithmes de soustraction
\(631 - 439\)
L’élève décompose le second terme et soustrait par étapes.
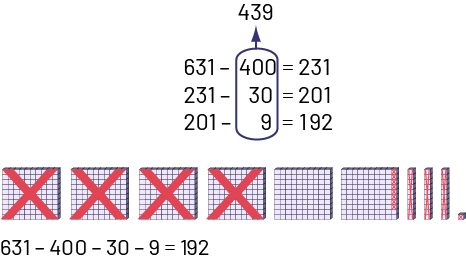
Image 3 soustractions sont superposées. 631 moins 400 égal 231. 231 moins 30 égal 201. 201 moins 9 égal 192. Tous les deuxièmes nombres des soustractions sont encerclés et additionnés pour un total de 439. Dix blocs de centaines sont alignés. 4 d’entre eux sont marqués d’une croix rouge. 3 colonnes de dix sont marquées d’une croix rouge ainsi que neuf blocs d’unités. Une soustraction : 631 moins 400 moins 30 moins, 9 égal 192.
L’élève additionne pour soustraire.
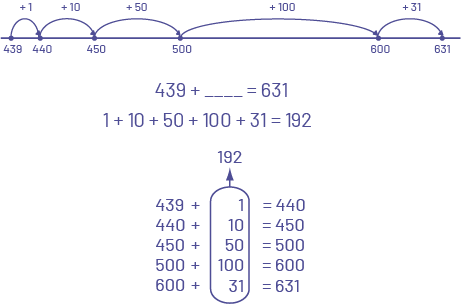
Image Une droite numérique qui commence à 439 et termine à 631, sans intervalle régulier. Des flèches sont placées pour représenter des bonds. De 439 à 440, bond de plus un. De 440 à 450, bond de plus dix. De 450 à 500, bond de plus 50. De 500 à 600, bond de plus 100. De 600 à 631, bond de plus 31. 439 plus nombre égal 631. Un plus dix, plus 50 plus, 100 plus 31 égal 192. Des additions sont superposées : 439 plus un égal 440. 440 plus dix égal 450. 450 plus 50 égal 500. 500 plus 100 égal 600. 600 plus 31 égal 631. Tous les deuxièmes nombres sont encerclés et additionnés pour un total de 192.
L’élève décompose le 1er terme et soustrait par étapes.
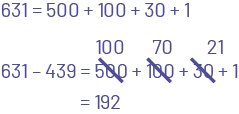
Image 631 égal 500 plus 100 plus 30 plus un. 631 moins 439 égal 500 « barré et remplacé par 100», plus 100 « barré et remplacé par 70 », plus 30 « barré et remplacé par 21», plus un. Égal 192.
L’élève utilise la droite numérique et note ses déplacements.
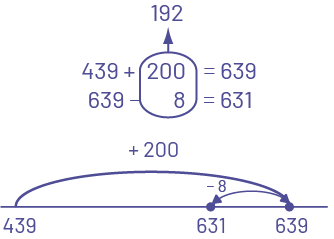
Image 439 plus 200 égal 639. 639 moins 8 égal 631. 200 et un sont encerclés et soustraits, c’est égal à 192. Sur une droite numérique de 439 à 639, sans intervalles réguliers, des flèches représentent les bonds suivants : De 439 à 639, bond de plus 200. De 639 à 631 bonds de moins 8.
L’élève utilise la droite numérique et compte à rebours à partir du plus grand nombre.
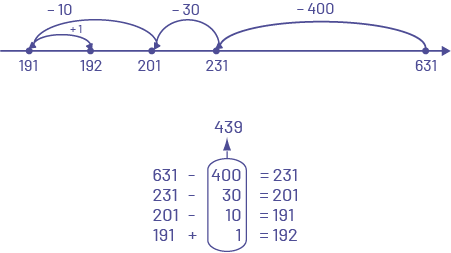
Image Droite numérique de 191 à 631, sans intervalle régulier. Des flèches représentent des bonds : de 191 à 192, un bond de plus un. de 631 à 231, un bond de moins 400. de 231 à 201, un bond de moins 30. de 201 à 191, un bond de moins dix Des phrases numériques sont superposées : 631 moins 400 égal 231. 231 moins 30 égal 201. 201 moins dix égal 191. 191 plus un égal 192 Tous les deuxièmes nombres sont encerclés, et additionnés pour un total de 439.
Source : Les mathématiques… un peu, beaucoup, à la folie!, Guide pédagogique, Édition révisée, Numération et sens du nombre, 3e année, Module 3, Série 2, Activité 4 - Dans l’entrepôt de l’usine, p. 450.
Les élèves peuvent utiliser le principe de compensation qui découle de la relation d’égalité. Il s’agit de modifier les termes d’une opération sans pour autant en modifier le résultat. Le principe de compensation fait en quelque sorte appel à la conservation de l’égalité des quantités lors d’opérations entre les nombres.
Selon ce principe, on peut modifier les parties d’une addition sans en changer la somme. Par exemple, pour calculer \(143 + 218\), on peut intervenir sur le nombre 143 de manière à faciliter le calcul. Pour ce faire, on soustrait 3 du 1er terme et on additionne 3 au 2e terme. De façon concrète, si on considère qu’on a 143 objets dans une pile et 218 objets dans une 2e pile, on déplace 3 objets de la 1re pile vers la 2e pile. Le nombre total n’a pas changé. L’expression numérique devient donc \(140 + 221\). Voici la phrase mathématique qui illustre ce qui se produit : \(143 + 218 = 143 - 3 + 218 + 3\). Donc, \(143 + 218 = 140 + 221\), pour une somme de 361.
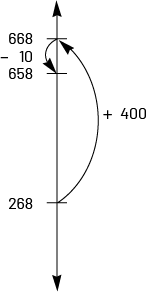
On utilise la compensation pour rendre une expression plus facile à évaluer. On peut s’en servir pour ajouter une quantité afin d’obtenir un nombre plus facile à manipuler, comme un multiple de 10 ou de 25, et soustraire la même quantité à la fin. Dans l’exemple suivant, on ajoute 10 au nombre 390 pour obtenir le nombre 400, qui est facile à additionner. On soustrait ensuite 10 de la réponse obtenue.
\(268 + 390 = \mathord{?}\)
\(268 + 400 = 668\)
\(668 - 10 = 658\)
Donc, \(268 + 390 = 658\)
On peut visualiser la situation en utilisant une droite numérique verticale. On voit que dans ce cas, un nombre supérieur à celui de l’expression (\(+ 400\)) a été ajouté. Le résultat recherché a ainsi été dépassé. Il faut donc retrancher l’excédent (\(-10\)).
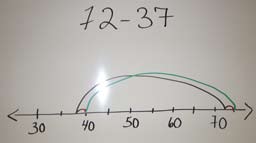
La compensation s’applique aussi à la soustraction. Puisqu’on cherche la différence entre les termes, on modifie les 2 termes de la même façon pour conserver la même différence. On peut ajouter une même quantité aux 2 termes ou on peut soustraire une même quantité des 2 termes. Par exemple, pour calculer \(72 - 37\), on peut ajouter 3 à 72 pour obtenir un nombre plus familier, soit 75, tout en additionnant 3 à 37 afin de maintenir le même écart.
\(72 - 37 = (72 + 3) - (37 + 3)\)
\(72 - 37 = 75 - 40\)
\(72 - 37 = 35\)
Pour cette même expression, on pourrait aussi compenser en soustrayant 2 de chaque terme.
\(72 - 37 = (72 - 2) - (37 - 2)\)
\(72 - 37 = 70 - 35\)
\(72 - 37 = 35\)
On peut aussi utiliser la compensation pour soustraire un plus grand nombre que ce qui est demandé dans l’expression mathématique pour ensuite ajouter à la différence. Dans l’exemple suivant, on soustrait 53 (3 de plus qu’il ne faut) pour faciliter la soustraction. On ajoute ensuite 3 au résultat.
\(173 - 50 = \mathord{?}\)
\(173 - 53 = 120\)
\(120 + 3 = 123\)
Donc, \(173 - 50 = 123\)
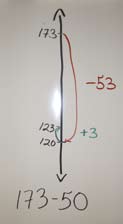
La compensation dans la soustraction fait appel au principe de la différence constante, à savoir que l’écart entre 2 nombres est le même si on leur ajoute ou si on leur enlève une même quantité (par exemple, la différence entre 645 et 185 est la même que celle entre 650 et 190 ou que celle entre 640 et 180).
Le concept de différence constante peut servir pour effectuer des opérations telles que la soustraction avec des 0 (par exemple, \(1000 - 354 = 999 - 353\)).

Source : Guide d’enseignement efficace des élèves de la 4e à la 6e année, p. 99-101.
Les exemples ci-dessus donnent une idée des différentes démarches que les élèves pourraient utiliser pour élaborer leurs propres algorithmes. Il faut se rappeler que l’utilisation d’un algorithme est un moyen efficient et efficace d’effectuer une opération arithmétique. Les algorithmes que créent les élèves ne sont pas nécessairement efficients et efficaces. Certains peuvent, par exemple, exiger plus d’étapes et plus de temps que nécessaire. Cependant, les élèves élaborent de tels algorithmes parce qu’elles et ils ont du sens pour eux. À force de partager et de comparer leurs stratégies, les élèves trouvent des méthodes de plus en plus efficientes et efficaces. Une méthode efficiente est une méthode qui requiert peu d’opérations arithmétiques et peu de temps pour arriver à la réponse. Une méthode efficace est une méthode qui s’applique à toutes les questions de ce type, autrement dit, elle est généralisable aux questions relevant de la même opération.
Pour les jeunes élèves, apprendre les opérations sur les nombres à plusieurs chiffres peut être une introduction positive ou négative aux mathématiques plus complexes et plus formelles qui leur seront enseignées au cours des années suivantes. Les opérations sur les nombres à plusieurs chiffres sont souvent une source de frustration pour les élèves qui perçoivent difficilement les liens entre les opérations arithmétiques et la résolution de problèmes. Il est donc important de recourir à une approche équilibrée faisant appel à l’apprentissage guidé, partagé et autonome pour enseigner ces opérations et donner aux élèves la chance de les comprendre et d’en saisir l’utilité.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 45.
Les algorithmes usuels
Bien que les algorithmes créés par les élèves leur permettent d’élaborer des stratégies arithmétiques qui leur conviennent, la plupart des gens sont plus habitués à l’algorithme usuel d’Amérique du Nord qui leur a été enseigné à l’école. Ce n’est qu’après avoir acquis un sens du nombre et une bonne connaissance des stratégies personnelles pour effectuer les opérations arithmétiques de base que les élèves peuvent être initiés à « l’algorithme usuel ». Lorsqu’on initie les élèves aux algorithmes usuels, il est important de les aider à acquérir une bonne compréhension des opérations plutôt que de leur demander simplement de mémoriser des règles. Certains élèves préféreront utiliser l’algorithme usuel, alors que d’autres continueront à utiliser les stratégies souples élaborées en classe.
Plusieurs considérations devraient être prises en compte lorsqu’on présente les algorithmes usuels aux élèves :
Apprentissage antérieur – Il faut que les élèves aient eu de multiples expériences leur ayant permis d’inventer des algorithmes souples pour effectuer une opération.
Langage mathématique – Des termes comme « emprunt » et « retenue » sont trompeurs. Il est préférable de parler « d’échange et de regroupement ». Il faut porter une attention particulière à la façon de nommer le chiffre des dizaines dans un nombre à 2 chiffres lorsqu’on décrit une opération. Il arrive que des élèves tombent dans le piège et nomment le chiffre des dizaines par son vocable de simple chiffre. Ainsi, au lieu de dire « Soustraire 20 de 30 » pour expliquer la réponse à un problème comme \(35 - 22\), ces élèves disent « Soustraire 2 de 3 ». Cela crée une méprise conceptuelle qui risque de perdurer, en particulier lorsque les élèves travaillent avec des nombres plus complexes, comme des nombres décimaux (les élèves du cycle moyen ont souvent de la difficulté à déterminer si la réponse à un problème est 0,32; 3,2 ou 32,0).
Valeur de position – La plupart des algorithmes usuels font appel au regroupement par dizaines, par centaines et ainsi de suite. Les élèves ont besoin d’utiliser du matériel de manipulation dans des activités qui portent sur le regroupement pour bien comprendre la valeur de position.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 54-55.
Pour décider s’il vaut mieux utiliser l’algorithme usuel ou un algorithme personnel, il faut toujours réfléchir à la situation et aux nombres utilisés. Lorsqu’il s’agit de remettre de la monnaie sur un achat au magasin, par exemple, le recours à un algorithme souple qui consiste à compter à partir du coût de l’achat jusqu’au montant versé par le client ou la cliente est beaucoup plus efficace que l’algorithme usuel, du moins pour les soustractions de nombres à plusieurs chiffres. De même, on considérera sans doute qu’il n’est pas nécessaire d’utiliser les étapes complexes enseignées dans l’algorithme usuel pour effectuer un calcul comme \(1 000 - 10\) ; un simple compte à rebours par 10 donnera la réponse la plus rapide pour toute personne qui sait ce qu’elle fait et pourquoi elle le fait. En revanche, pour effectuer un calcul comportant plusieurs nombres, il peut être plus approprié d’utiliser l’algorithme usuel et de faire le calcul sur papier.
Stratégies pour faciliter la compréhension des algorithmes usuels
Il est important de proposer aux élèves plusieurs activités d’exploration des algorithmes usuels en utilisant du matériel de manipulation tel que le tapis de valeur de position, les cubes emboîtables, les cadres à 10 cases, le matériel de base 10, la droite numérique, etc.
Le personnel enseignant doit leur fournir plusieurs occasions de créer leurs propres algorithmes, d’expliquer leurs stratégies ainsi que les raisons qui motivent leurs choix. Il est primordial de donner aux élèves la chance et le temps d’explorer plus en profondeur les algorithmes et de favoriser les échanges. Il est important de les encourager à travailler à 2 (un ou une élève prend en note les étapes de la démarche alors que l’autre travaille avec la représentation concrète). La compréhension du sens des étapes d’un algorithme usuel se développe lorsque le personnel enseignant permet aux élèves de le comparer à leur propre algorithme afin d’établir des liens entre les 2 démarches comme « additionner de gauche à droite et combiner ».
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 56.
Addition sur les nombres à plusieurs chiffres sans regroupement
Une addition de grands nombres peut être représentée sur une droite numérique. Par exemple, les élèves pourraient effectuer \(435 + 223\) en décomposant 223 (\(200 + 15 + 8\)) et en représentant l’opération comme suit :


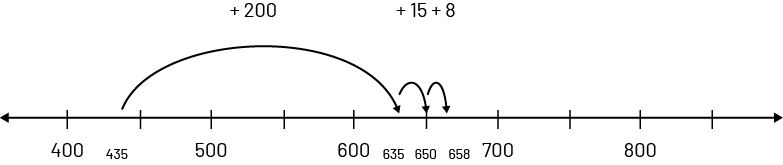
Image Droite numérique de 400 à 800 par intervalles de 50. Des flèches représentent des bonds. de 435 à 635, un bond de plus 200. de 635 à 650, bond de plus 15. de 650 à 658, bond de plus 8. Au fil du temps, les élèves développent progressivement leur sens de l’abstraction et peuvent utiliser la même stratégie sans avoir recours à une droite numérique, mais en effectuant le calcul mentalement.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 122-123.
Addition sur les nombres à plusieurs chiffres avec regroupement
(Van de Walle et Folk, 2005, p. 191)
Il est important que les élèves puissent s’exercer à échanger des groupes de 10 unités en dizaines, des groupes de 10 dizaines en centaines, etc. Elles et ils ont besoin de l’appui de représentations visuelles de regroupements afin de développer une compréhension conceptuelle de l’algorithme.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 57.
Le matériel de base 10 aide certains élèves à visualiser l’opération plus clairement. Voici comment le matériel de base 10 peut servir pour représenter les additions.
Exemple
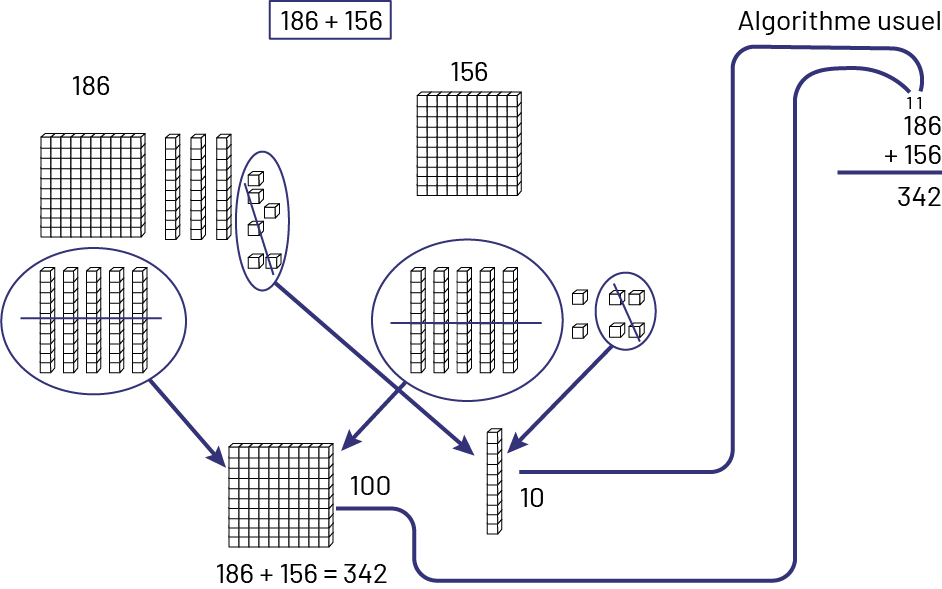
Image 186 plus 156. 186 est représenté par un bloc de centaine, 8 blocs de dizaines et 6 unités. 156 est représenté par un bloc de centaines, 5 blocs de dizaines et 6 blocs d’unité. 5 blocs de dizaines de 186 ainsi que 156 sont encerclés et sont transformés en un bloc de centaine. 6 blocs d’unité de 186 et 4 blocs d’unité de 156 sont transformés en un bloc de dizaine. 186 plus 156 égal 342. Algorithme usuel. 186 plus 156, retenues de un au-dessus des dizaines et un au-dessus des centaines.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 123.
Soustraction sans échange
Comme pour l’addition, les élèves utilisent souvent du matériel de manipulation pour effectuer des soustractions. Cette stratégie les aide à saisir le concept de retrait, même si elle n’est pas très efficace lorsqu’il s’agit de grands nombres.

Image 60 moins 28. Des jetons sont utilisés comme matériel de manipulation. Les jetons sont divisés en 3 sections, une main fait glisser un jeton d’une section à une autre. 60 moins 28 égal 32.
Le matériel de base 10 permet aux élèves d’effectuer la soustraction au moyen d’un retrait.
Exemple
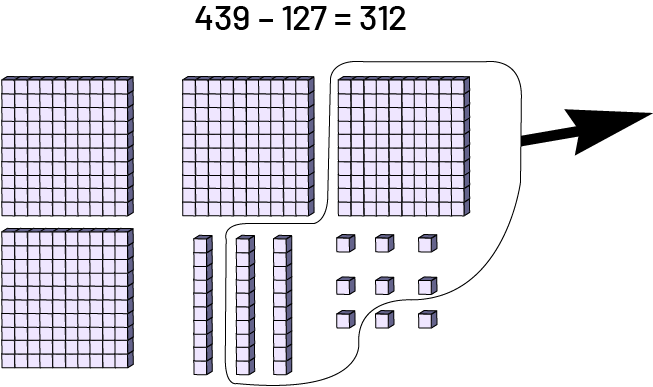
Image 439 moins 127 égal 312. 4 blocs de centaines, 3 blocs de dizaine, et 9 blocs d’unité. Un bloc de centaine, 2 blocs de dizaine et 7 blocs d’unité sont encerclés et une flèche démontre la soustraction. Si le tapis de valeur de position pour la soustraction est utilisé, certaines et certains élèves sont portés à représenter les 2 termes. La soustraction est alors effectuée par comparaison.
Exemple

Image 439 moins 127 égal 312. Dans un tableau de 2 rangées et 3 colonnes. Dans la première case, 4 blocs de centaines, un trait, place un bloc dans la case en dessous. Dans la deuxième case, 3 blocs de dizaine, un trait, place 2 blocs dans la case en dessous. Dans la troisième case, 9 blocs d’unité, un trait, place 7 blocs dans la case en dessous.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 127-128.
Soustraction avec échange
(Van de Walle et Folk, 2005, p. 191)
L’exploration de la soustraction avec échange en favorise la compréhension conceptuelle. Le personnel enseignant devrait encourager les élèves à utiliser le tapis de valeur de position et du matériel de base 10 pour modéliser la soustraction avec échange. Les élèves peuvent travailler à 2. Elles et ils peuvent passer à la forme écrite de l’algorithme une fois qu’elles et ils en ont développé une solide compréhension par l’entremise de modèles.
Dans le cas du problème \(325 - 118\), les élèves représentent le 1er nombre (325) avec du matériel de base dix sur la portion supérieure du tapis de valeur de position. Ne pouvant pas retirer 8 unités puisqu’il n’y en a que 5, les élèves échangent une dizaine pour 10 unités.
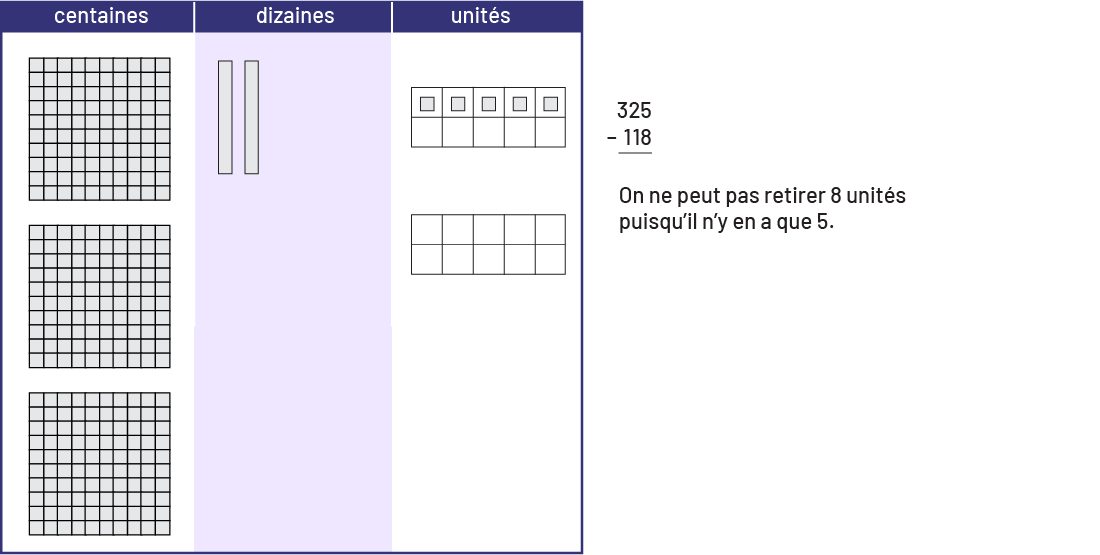
Image Dans un tapis de valeurs, des blocs ont été placés. Dans la section des centaines, 3 blocs. Dans la section des dizaines, un bloc. Dans la section des unités 5 blocs. 325 moins 118 égal. On ne peut pas retirer 8 unités puisqu’il n’y en a que 5.
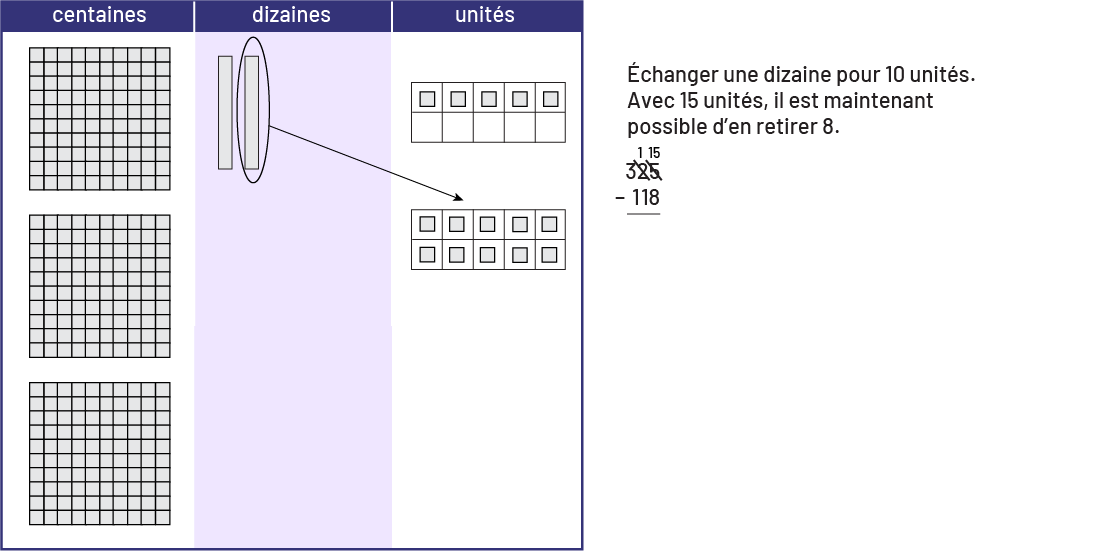
Tapis de valeurs, des blocs ont été placés. Dans la section des centaines, 3 blocs. Dans la section des dizaines, 2 blocs. Dans la section des unités, 5 blocs. Un bloc de dizaine est encerclé et transféré dans la section des unités. Échanger une dizaine pour dix unités. Avec 15 unités, il est maintenant possible d’en retirer 8. 325 moins 118
Elles et ils obtiennent ainsi un groupe de 15 unités à partir duquel il leur est maintenant possible d’en retirer 8 de sorte qu’il en reste 7. Il faut encourager les élèves à regrouper les unités sur le tapis afin de mieux organiser leur travail.
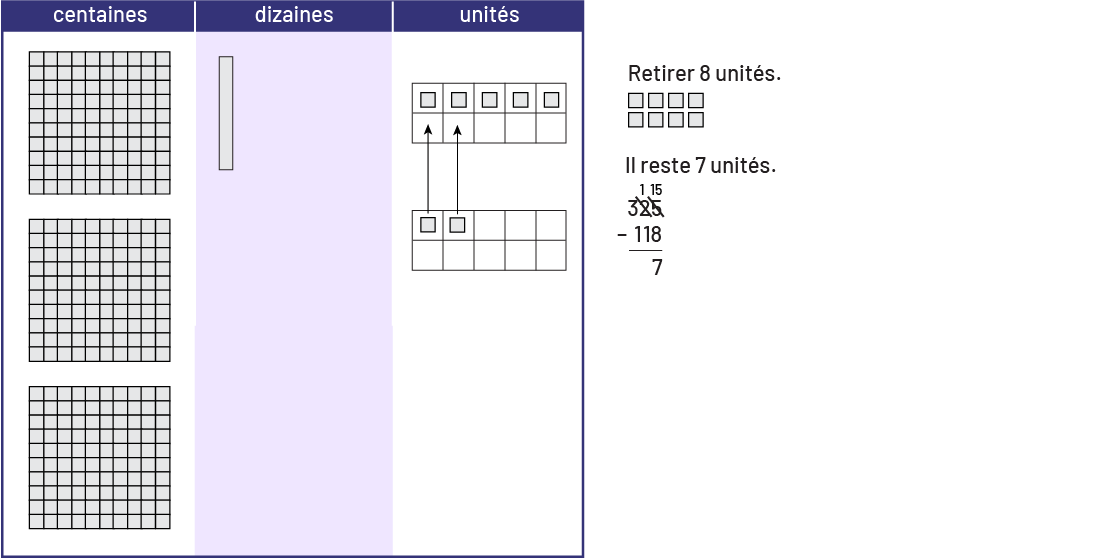
Image Sur un tapis de valeur, où sont placés des blocs. Dans la section des centaines, 3 blocs. Dans la section des dizaines, un bloc. Dans la section des unités, 7 unités. Retirer 8 unités. 8 blocs d’unités. Il reste 7 unités.325 moins 118 égal 7 unités.
Les élèves retirent maintenant une dizaine et une centaine et les placent à l’extérieur du tapis.
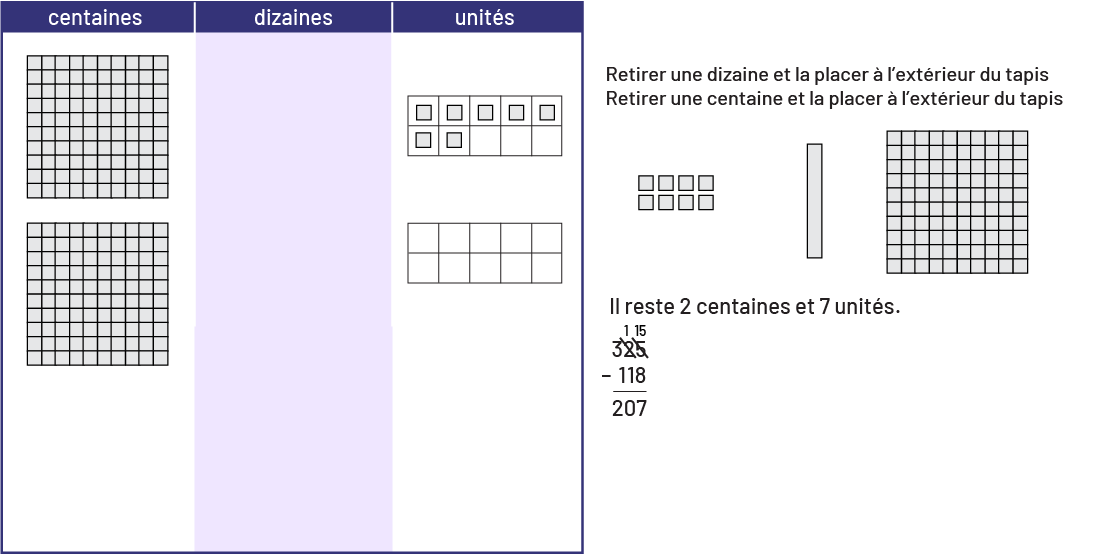
Image Sur un tapis de valeurs, où sont placés des blocs. Dans la section des centaines, 2 blocs. Dans la section des dizaines, c’est vide. Dans la section des unités, 7 blocs. Retirer une dizaine et la placer à l’extérieur du tapis. Retirer une centaine et la placer à l’extérieur du tapis. 8 blocs d’unités, un bloc de dizaine, un bloc de centaine. Il reste 2 centaines et 7 unités. 325 moins 118 égal 201.
Donc, \(325 - 118 = 207\).
Les élèves peuvent aussi utiliser la droite numérique pour effectuer une soustraction. Par exemple, pour calculer \(263 - 45\), elles et ils peuvent utiliser la compensation afin de travailler avec des nombres plus familiers. Puisque \(263 + 2 = 265\), on peut donc effectuer \(265 - 45 = 220\) et ensuite, soustraire 2 pour compenser (\(263 + 2 - 45 - 2\)).
Les élèves n’ont pas à transcrire leur réflexion sous forme d’expression numérique, mais peuvent néanmoins utiliser la droite numérique pour illustrer leur démarche :
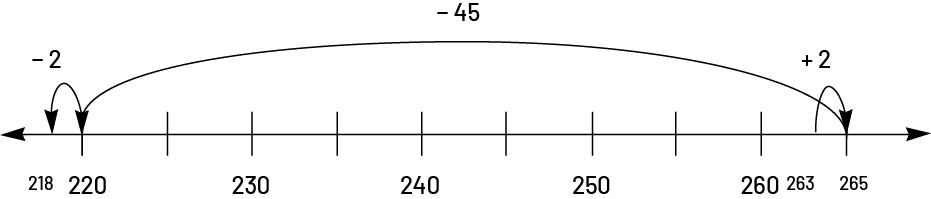
La droite numérique peut également être employée avec la décomposition selon les valeurs de position des chiffres du nombre (\(263 - 40 = 223\), \(223 - 5 = 218\)) :
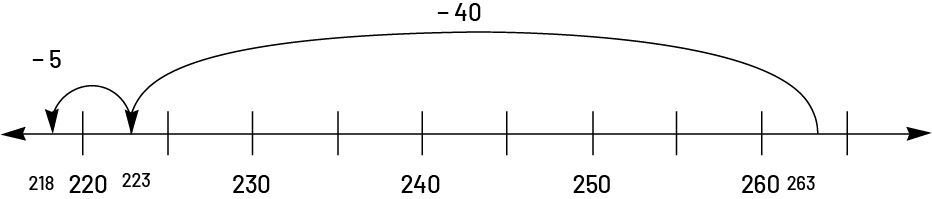
La droite numérique ouverte permet aux élèves de procéder par bonds significatifs (\(263 - 3 = 260\), \(260 - 40 = 220\), \(220 - 2 = 218\)) :
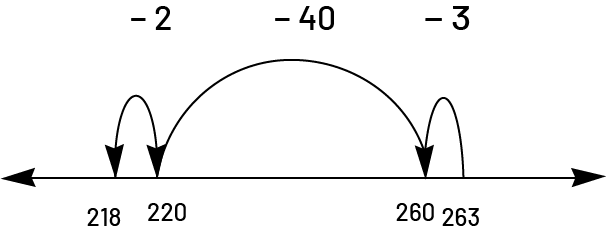
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 127.
Les élèves peuvent utiliser des dessins pour illustrer rapidement une expression numérique comme \(969 - 421\). Les nombres peuvent être représentés par des lignes, des cercles, des points, etc. Un retrait peut être exprimé par des barres sur le dessin. Pour \(969 - 421\), il faut enlever 4 centaines, 2 dizaines et 1 unité des 9 centaines, 6 dizaines et 9 unités.
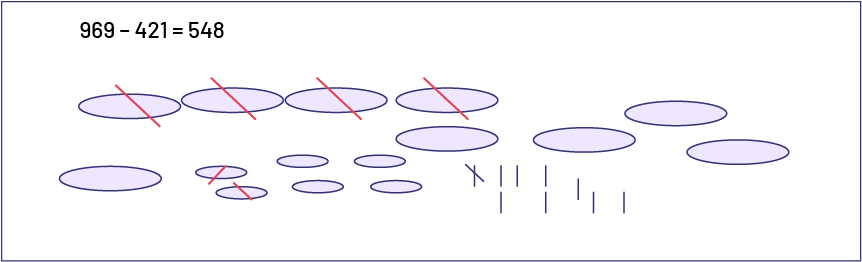
Image 969 moins 421 égfal 548. Une illustration représente la phrase mathématique. 9 gros ovales, 6 petits ovales et 9 bâtonnets. 4 gros ovales sont barrés, ainsi que 2 petits ovales et un bâtonnet.
