B2.5 Représenter et résoudre des problèmes relatifs à l’addition de nombres naturels dont la somme est égale ou inférieure à 1 000 et à la soustraction de nombres naturels égaux ou inférieurs à 1 000, à l’aide d’une variété d’outils et d’algorithmes.
Habileté : représenter, décrire et résoudre des problèmes relatifs à l’addition et à la soustraction
En plus d’enseigner les opérations arithmétiques à partir de stratégies et du raisonnement s’y rattachant, il est important de présenter ces opérations dans des contextes de résolution de problèmes. Lors de la résolution de problèmes, on encourage les élèves à utiliser les connaissances déjà acquises et à établir des liens avec le nouvel apprentissage. Ces liens peuvent être rompus si on ne présente pas aux élèves un éventail diversifié de problèmes. Les élèves qui n’apprennent pas à calculer dans des contextes de résolution de problèmes pourraient avoir beaucoup de difficulté à faire ces liens plus tard. Leur compréhension de la notion abstraite du nombre et de son application risque d’être floue, et il est possible que certains n’arrivent pas à utiliser efficacement des stratégies de calcul pour résoudre des problèmes.
Le recours à des contextes de résolution de problèmes est tout aussi important pour les opérations sur les nombres à plusieurs chiffres. Lorsqu’on donne des problèmes aux élèves, lorsqu’on les encourage à trouver un algorithme et à l’utiliser de manière souple, on leur donne l’occasion d’approfondir leur compréhension des opérations. Par souci d’efficacité et croyant bien faire, on enseigne souvent aux élèves l’algorithme à utiliser pour effectuer les opérations sur les nombres à plusieurs chiffres. Cette méthode leur étant présentée comme la « bonne façon » de résoudre le problème, les élèves font des efforts ardus pour comprendre et mémoriser cette procédure. Cette méthode entraîne souvent une utilisation peu efficace de l’algorithme, un manque d’exactitude et une compréhension limitée. Si, au contraire, on encourage les élèves à dégager le sens du problème et à élaborer leurs propres stratégies pour le résoudre, elles et ils démontreront plus d’aisance et plus de précision dans leur travail sur les opérations.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 5.
Cela leur permettra de développer et d’explorer diverses stratégies ou divers algorithmes personnels.
Pour développer des stratégies efficaces chez les élèves, il est important d’offrir aux élèves divers types de problèmes de manière à leur permettre de saisir les multiples sens des opérations. Un problème bien choisi et l’application d’une stratégie réfléchie sont plus profitables qu’une série d’exercices complétés mécaniquement. Il faut ainsi allouer aux élèves le temps nécessaire pour comprendre et consolider les stratégies.
L’exploration de stratégies (incluant les algorithmes personnels) est essentielle puisque celles-ci sont des exemples tangibles du sens du nombre et du sens des opérations que les élèves ont acquis. Ces stratégies et ces algorithmes personnels indiquent comment elles et ils « jouent » avec les nombres et les opérations. Ces stratégies qui sont mises sur papier ont le potentiel de se transposer en stratégies de calcul mental. Par exemple, les élèves qui ont l’occasion d’écrire leur raisonnement sur papier ou qui utilisent une grille de nombres pour effectuer un calcul tel que \(36 + 52\) pourront ultérieurement suivre un raisonnement similaire mentalement.
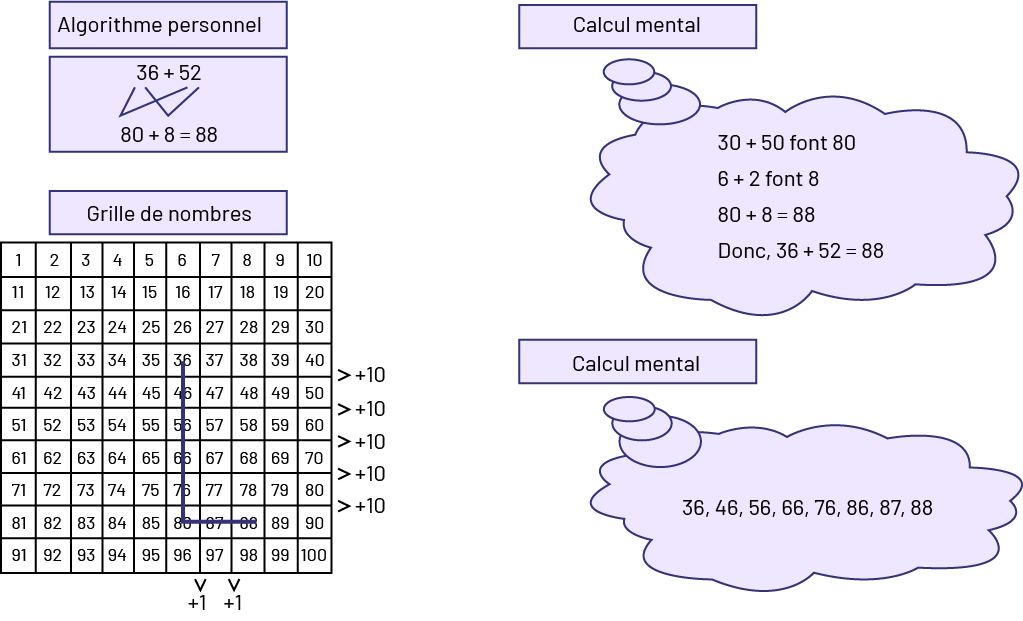Image Algorithme personnel : 36 plus 52, les dizaines sont additionnées, ainsi que les unités, on
obtient 80 plus 8
égal 88. Grille de nombres, de, un à 100. Un trait est tracé sur les nombres 36, 46, 56, 66, 76, 86, 87, 88. « plus
dix» sont entre les cases 40 et 50, 50 et 60, 60 et 70, 70 et 80, 80 et 90. « plus un » est entre 96 et 97, et 97 et
98. Calcul mental. 30 plus 50 font 80. 6 plus 2 font 8. 80 plus 8 font 88 Donc, 36 plus 52 égal 88. Calcul mental. 36,
46, 56, 66, 76, 86, 87, 88.
De plus, il est essentiel d’animer des échanges mathématiques portant, par exemple, sur ces stratégies et sur les algorithmes personnels. Ces échanges favorisent le partage de stratégies et la reconnaissance de liens entre elles. Les stratégies personnelles de chaque élève se précisent, se perfectionnent et deviennent plus efficaces au fur et à mesure qu’elle ou il établit des liens entre elles. Ainsi, « le personnel enseignant oriente la discussion en ayant recours à des stratégies qu’ont utilisées des élèves pour amorcer la compréhension de concepts mathématiques précis et pour diriger la progression des élèves vers des méthodes efficaces » (Ministère de l’Éducation de l’Ontario, 2004 a, p. 18).
Le rôle du personnel enseignant est alors d’aider les élèves à organiser leurs traces. Par exemple, on peut amener les élèves à utiliser des représentations semi-concrètes, en faisant ressortir qu’un ou une élève qui a regroupé des objets présente le même raisonnement que celui ou celle qui a écrit le nombre en guise de regroupement.
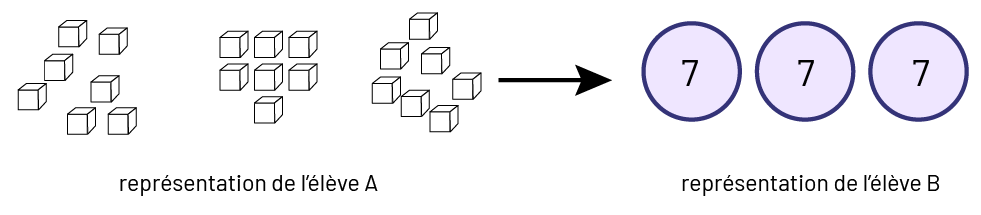
De même, lorsqu’un ou une élève prend physiquement 10 groupes de 10 unités, qu’elle ou il constate qu’il s’agit d’un groupe de 100 unités et qu’elle ou il l’appelle centaine, on peut mentionner qu’elle ou il utilise le concept de regroupement et qu’il s’agit du même regroupement qui est symbolisé par l’écriture du chiffre « 1 » au-dessus de la position des centaines dans l’algorithme usuel.
Image 31 plus 164 plus 47 égal. 2 blocs de centaines, 13 blocs de dizaines et 12 blocs d’unités. Dix blocs de dizaine sont encerclés. Une flèche pointe du cercle vers un bloc de centaine, et une autre flèche pointe du bloc de centaine vers l’addition.
L’étayage par le personnel enseignant permet aux élèves de comprendre les concepts sous-jacents associés aux diverses opérations (par exemple, échange dans la soustraction). De plus, l’échange mathématique permet de présenter de nouvelles stratégies. Le personnel enseignant et les élèves peuvent aussi modeler des stratégies en s’assurant de verbaliser le raisonnement qui s’y rattache. Ultérieurement, l’algorithme usuel peut être présenté en s’assurant que les élèves comprennent les concepts sous-jacents et les raisons des gestes posés. Les algorithmes usuels doivent être perçus par les élèves comme étant seulement une autre façon d’effectuer les opérations.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 76-78.
Problèmes écrits relatifs à l’addition et à la soustraction
Dans l’addition ou la soustraction, des quantités sont ajoutées, retirées, unies ou comparées. Pour que les élèves comprennent les liens entre les quantités dans chacun de ces cas, il est important qu’elles et ils soient confrontés à divers types de problèmes. Ci-dessous se trouvent une variété de problèmes relatifs à l’addition et à la soustraction.
L’addition et la soustraction ne sont que des opérations qui surviennent dans des problèmes. Il faut donc éviter de parler de « problèmes de soustraction » ou « problèmes d’addition », car c’est la compréhension de la situation, ainsi que la compréhension des opérations qui font choisir la stratégie de résolution de problèmes à adopter, en l’occurrence le choix de l’addition ou de la soustraction. Donc, les élèves doivent analyser le problème, choisir une stratégie et l’appliquer, tout comme le font les adultes. Dans ce contexte, le rôle du personnel enseignant est d’aider les élèves dans leur analyse et dans leur compréhension des opérations.
Il est important de noter que les problèmes présentés dans le tableau semblent similaires en raison de leur contexte. Or pour les élèves, chaque situation représente un problème particulier. C’est en maîtrisant ces divers types de problèmes que les élèves acquièrent une maîtrise de l’addition et de la soustraction.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 81.
Problèmes d’ajout
Le modèle partie-tout peut être utile pour représenter les valeurs connues et inconnues dans des problèmes d’ajout. Le modèle d’ensemble est utile pour représenter l’ajout d’une quantité.
- Ajout : valeur finale inconnue
Jamil a 6 bonbons. Il en achète 5 de plus. Combien de bonbons Jamil a-t-il à présent?
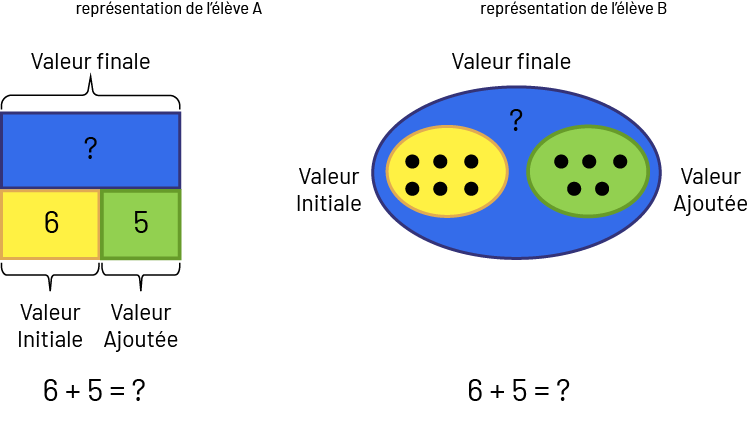Image Représentation de l’élève « A ». Valeur finale : un bloc bleu représente une inconnue, en
dessous un bloc jaune d’une valeur de 6, et un bloc vert
d’une valeur de 5. Le 6 est la valeur initiale et le 5 la valeur ajoutée. 6 plus 5 égal inconnue. Représentation de
l’élève « B » : Valeur finale : un ovale bleu représente une inconnue. Dans cet ovale, il y a deux autre ovales plus
petits, un jaune
qui contient 6 points noirs, c’est la valeur initiale. Et un vert qui contient 5 points noirs, c’est la valeur
ajoutée. 6 plus 5 égal inconnue.
- Ajout : valeur initiale inconnue
Jamil a quelques bonbons. Il en achète 5 de plus. Il en a 11 à présent. Combien de bonbons Jamil avait-il au début?
Image Valeur finale: un bloc bleu dont la valeur est 11. En dessous : un bloc jaune de valeur
inconnue, c’est la valeur initiale. un bloc vert sa valeur est 5, c’est la valeur ajoutée. Inconnue plus 5 égal
11.
- Ajout : valeur ajoutée inconnue
Jamil a 6 bonbons. Il en achète quelques-uns de plus. Il en a 11 à présent. Combien de bonbons Jamil a-t-il achetés?
Image Valeur finale: un bloc bleu dont la valeur est 11. En dessous : un bloc jaune sa valeur est
de 6, c’est la valeur initiale. un bloc vert sa valeur est inconnue, c’est la valeur ajoutée. 6 plus inconnue égal
11.
Problèmes de retrait
Le modèle partie-tout peut être utile pour représenter les valeurs connues et inconnues dans des problèmes de retrait. Le modèle d’ensemble est utile pour représenter le retrait d’une quantité.
- Retrait : valeur finale inconnue
Nadia a 150 $. Elle donne 50 $ à son frère. Combien lui reste-t-il de dollars à présent?
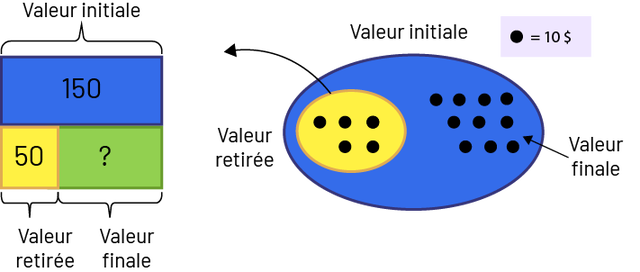Image Valeur initiale: un bloc bleu dont la valeur est 150. En dessous : un bloc jaune sa valeur
est de 50, c’est la valeur retirée. un bloc vert sa valeur est inconnue, c’est la valeur finale. Un ensemble bleu
contient dix points noirs, et un petit ovale jaune qui contient 5 points noirs. L’ensemble est la
valeur initiale, l’ovale jaune est la valeur retirée, les points noirs de l’ensemble bleu la valeur finale. Un point
noir égal dix dollars.
\(150 - 50 = \mathord{?}\)
- Retrait : valeur retirée inconnue
Nadia a 150 $. Elle donne quelques dollars à son frère. Il lui reste 100 $ à présent. Combien de dollars Nadia a-t-elle donnés à son frère?
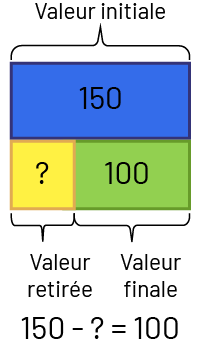Image Valeur initiale: bloc bleu de valeur 150. En dessous un bloc jaune de valeur inconnue, c’est
la valeur retirée.
Et un bloc vert de valeur 100, c’est la valeur finale. 150 moins inconnue égal 100.
- Retrait : valeur initiale inconnue
Nadia avait un certain nombre de dollars. Elle a donné 50 $ à son frère. Il lui reste 100 $ à présent. Combien de dollars Nadia avait-elle au début?
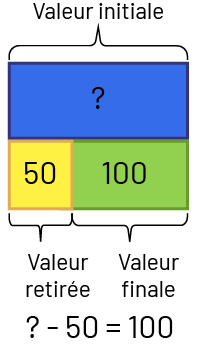Image Valeur initiale: bloc bleu de valeur inconnue. En dessous un bloc jaune de valeur de 50,
c’est la valeur retirée. Et un bloc vert de valeur de 100, c’est la valeur
finale. Inconnu moins 50 égal 100.
Problèmes de réunion
Le modèle partie-tout peut être utile pour représenter les parties du tout connues et inconnues ou le tout connu ou inconnu dans des problèmes de réunion.
- Réunion : partie du tout inconnue
La classe a beaucoup de crayons de couleur accumulés au courant des années. Il y a 800 crayons de couleur. 300 de ces crayons sont rouges. Les crayons qui restent sont bleus. Combien de crayons bleus la classe a-t-elle?
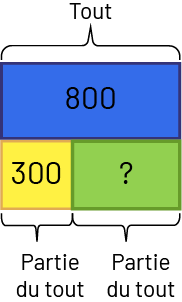Image Un tout est représenté par un bloc bleu d’une valeur de 800. En dessous, un bloc jaune d’une
valeur de 300,
c’est la partie du tout. Un bloc vert de valeur inconnue, c’est une partie du tout.
\(800 - 300 = \mathord{?}\)
- Réunion : tout inconnu
La classe a beaucoup de crayons de couleur accumulés au courant des années. Il y a 300 crayons rouges et 500 crayons bleus. Combien de crayons de couleur la classe a-t-elle?
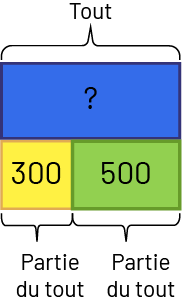Image Un
tout est représenté par un bloc bleu, d’une valeur inconnue. En dessous, un bloc jaune d’une valeur de 300, c’est une
partie du tout. Un bloc vert d’une valeur de 500, c’est une partie du tout.
\(\mathord{?} - 300 = 500\)
Problèmes de comparaison
Le modèle linéaire peut être utile pour représenter la différence entre 2 nombres dans des problèmes de comparaison. Dans cet exemple, on utilise les réglettes Cuisenaire et la droite numérique double.
- Comparaison : différence inconnue
Judith a 600 $ et Jeanne a 300 $. Combien de dollars Judith a-t-elle de plus que Jeanne? OU Judith a 600 $ et Jeanne a 300 $. Combien de dollars Jeanne a-t-elle de moins que Judith?
Je sais que la réglette verte foncée représente 6 (centaines), alors je la place en haut de la droite numérique en partant du 0. Je sais que la réglette vert lime représente 3 (centaines), alors je la place sous la droite numérique en partant du 0. Je compare les 2 réglettes et je vois que la réglette vert lime est 3 (centaines) de moins que la réglette verte foncée. Je trouve la différence ou l’écart entre les 2 quantités. Il y a une différence de 300 $. Judith a 300 $ de plus que Jeanne ou Jeanne a 300 $ de moins que Judith.
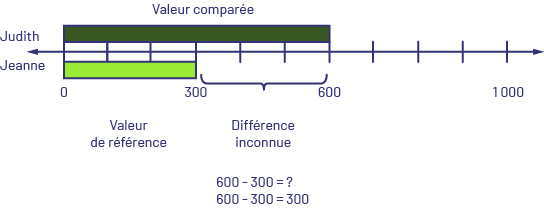Image Droite numérique, de zéro à 1000, avec des intervalles de 100. Une barre vert kaki
représente l’argent de Judith de zéro à 600 c’est la valeur comparée. Une barre vert pâle représente l’argent de
Jeanne de zéro à 300, c’est la valeur de référence. La différence inconnue est de 300 et 600. 6 moins 3 égal inconnue.
6 moins 3 égal 3.
- Comparaison : valeur comparée inconnue
Judith a 300 $ de plus que Jeanne. Jeanne a 300 $. Combien de dollars Judith a-t-elle? OU Jeanne a 300 $ de moins que Judith. Jeanne a 300 $. Combien de dollars Judith a-t-elle?
Je sais que la réglette vert lime représente 3 (centaines), alors je la place en haut de la droite numérique en partant du 0. Je prends une autre réglette vert lime et je la place sous la droite numérique en partant du 0 et j’ajoute une autre réglette vert lime puisque Judith a 300 $ de plus que Jeanne. Je remplace les 2 réglettes vert lime avec la réglette verte foncée qui représente 6 (centaines). Judith a donc 600 $.
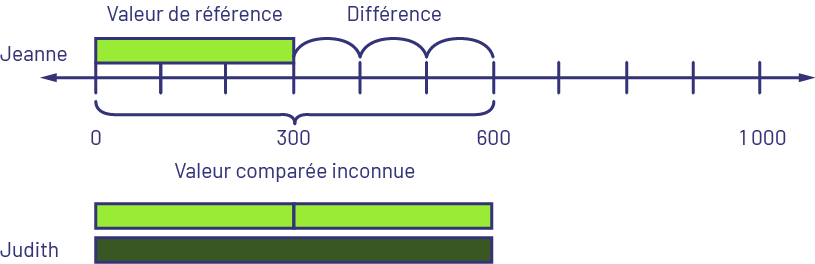Image Une droite numérique de zéro à 1000, par intervalles de 100. Une barre verte représente le
montant de Jeanne, c’est la valeur de référence de zéro à 300. Des bonds de 100 sont placés de 300 à 600 c’est la
différence. Une arabesque commence à zéro, son milieu est 300 et finit à 600. C’est la valeur comparée inconnue. Les
barres qui représentent la valeur du montant de Judith sont à côté de la barre de valeur de référence.
- Comparaison : valeur de référence inconnue
Judith a 600 $ et Jeanne a 300 $ de moins que Judith. Combien de dollars Jeanne a-t-elle? OU Jeanne a 300 $ de moins que Judith. Judith a 600 $. Combien de dollars Jeanne a-t-elle?
Je sais que la réglette verte foncée représente 6 (centaines), alors je la place en haut de la droite numérique en partant du 0. Sur la droite numérique, je compte à rebours de 3 bonds pour arriver à 300 pour représenter que Jeanne a 300 $ de moins que Judith. Je prends une réglette vert lime, qui représente 3 (centaines) et je la place sous la droite numérique en partant du 0. Jeanne a 300 $.
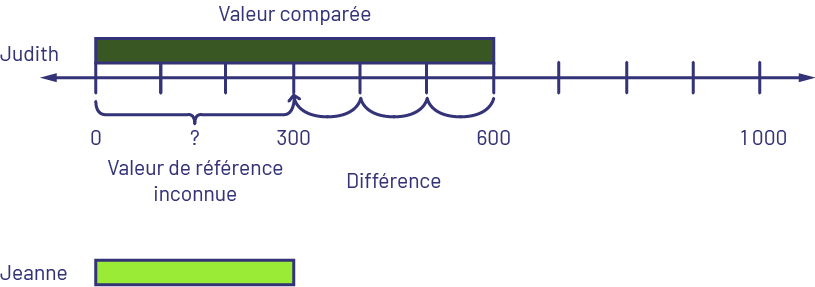
Image Une droite numérique de zéro à 1000, par intervalles réguliers de 100. Une barre verte kaki représente le montant de Judith, de zéro à 600, c’est la valeur comparée. Une parenthèse commence à zéro et finie à 300, c’est la valeur de référence inconnue. Des bonds de 100 de 300 à 600 représentent la différence. Une barre verte pâle représente le montant de Jeanne.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 9-10.
Les problèmes d’ajout et de retrait sont perçus par les élèves comme des situations actives, plus faciles à modéliser et à « voir », car la quantité initiale augmente ou diminue. Les problèmes de réunion, cependant, supposent une situation statique, car aucune action ou aucun changement ne se produit, ce qui les rend plus abstraits et plus difficiles à comprendre. Les problèmes de comparaison, quant à eux, traitent de la relation entre 2 quantités en les opposant : il n’y a donc pas d’action, mais une comparaison d’une quantité à une autre.
Puisque les élèves sont exposés régulièrement à des problèmes dont la quantité finale est recherchée, elles et ils les résolvent plus aisément. Cependant, elles et ils ont plus de mal à résoudre les problèmes dont l’inconnue est la quantité initiale, la quantité ajoutée ou la quantité retirée. Ces problèmes aident à développer une compréhension plus solide des opérations d’addition et de soustraction et des liens entre les opérations. Par exemple, dans le cas des problèmes d’ajout dont l’inconnue est la quantité initiale, les élèves voient plus facilement les avantages de l’addition (par exemple, \(\mathord{?} + 12 = 37\)) qui permet de respecter l’ordre dans lequel se déroule l’action dans le problème. Cela leur permet d’utiliser une stratégie (par exemple, dénombrement ou compte à rebours) afin de déterminer la quantité initiale. Ces élèves démontrent leur compréhension du problème et leur habileté à utiliser une stratégie pour le résoudre. Cependant, elles et ils ne démontrent pas une compréhension du sens de la différence (et de la soustraction). Si elles et ils avaient utilisé la soustraction, soit \(37 - 12 = \mathord{?}\), elles et ils auraient démontré une compréhension plus élargie des liens entre les quantités par rapport à cette opération. Cependant, lorsque les élèves sont en apprentissage, il est inutile de leur imposer une stratégie.
L’obligation de soustraire n’aidera en rien les élèves qui ne voient pas la pertinence de cette stratégie. Toutefois, si elles et s’ils sont régulièrement en contact avec une variété de problèmes et qu’elles et ils participent aux échanges mathématiques qui suivent, elles et ils arrivent à voir les liens entre diverses stratégies et à assimiler une variété de stratégies. Elles et ils deviennent alors plus performants.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 83-84.
Relation entre les opérations
Les opérations fondamentales, soit l’addition, la soustraction, la multiplication et la division sont intimement reliées malgré leurs différences apparentes. Plus les élèves ont l’occasion de manier les opérations, plus elles et ils peuvent remarquer et comprendre les liens entre elles.
L’addition et la soustraction sont des opérations inverses. Or, lorsqu’elles et ils sont en apprentissage, les élèves ont souvent de la difficulté à résoudre des équations telles que \(17 + \Delta = 31\). Plusieurs membres du personnel enseignant incitent alors leurs élèves à utiliser l’opération inverse, soit la soustraction. Or, il peut s’agir d’apprendre un truc, à moins que les élèves comprennent pourquoi la soustraction est une stratégie possible. Elles et ils doivent d’abord saisir la relation du tout et de ses parties ainsi que le sens d’une différence. Par exemple, un nombre peut être représenté comme suit :
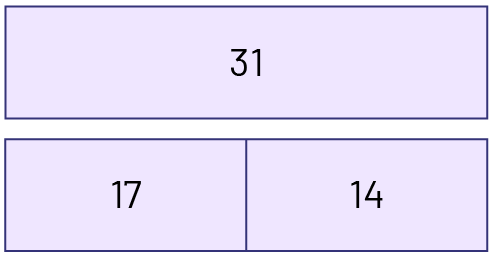
Cette façon de représenter la relation entre un nombre et ses parties permet de voir que la soustraction est l’opération inverse de l’addition. Ainsi, puisque \(17 + 14 = 31\) et \(14 + 17 = 31\), donc \(31 - 17 = 14\) et \(31 - 14 = 17\).
De plus, les élèves peuvent voir pourquoi l’addition est commutative \((14 + 17 = 17 + 14)\) et pourquoi la soustraction ne l’est pas \((31 - 17 \neq 17 - 31)\). Ceux qui ont acquis un bon sens du nombre et qui sont capables de décomposer et de regrouper des nombres peuvent mettre leurs connaissances à profit pour résoudre plus efficacement des équations telles que \(17 + \rule{1cm}{0.15mm} = 31\) en comprenant que l’on cherche la différence entre 17 et 31.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 97-98.
Connaissance : problème d’ajout
Dans les problèmes axés sur l’ajout, le résultat est le plus grand.
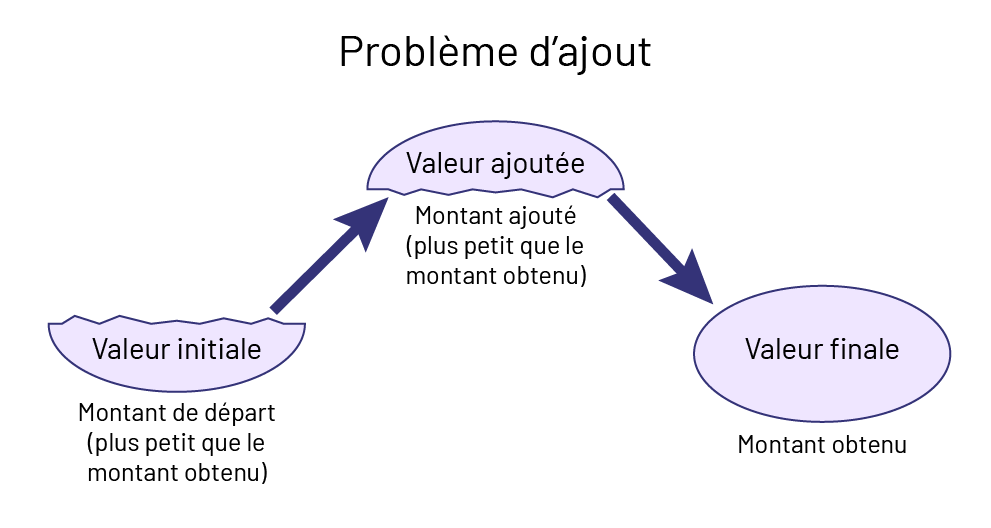Image Problème d’ajout.La valeur initiale, montant de départ (parenthèse ouvrante) plus petit que
le montant obtenu (parenthèse fermante).
Une flèche pointe vers, valeur ajoutée, montant ajouté (parenthèse ouvrante) plus petit que le montant obtenu
(parenthèse fermante). Une flèche pointe vers valeur finale, le montant obtenu.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p.9.
Connaissance : problème de retrait
Dans les problèmes de retrait, le 1er montant est le plus grand.
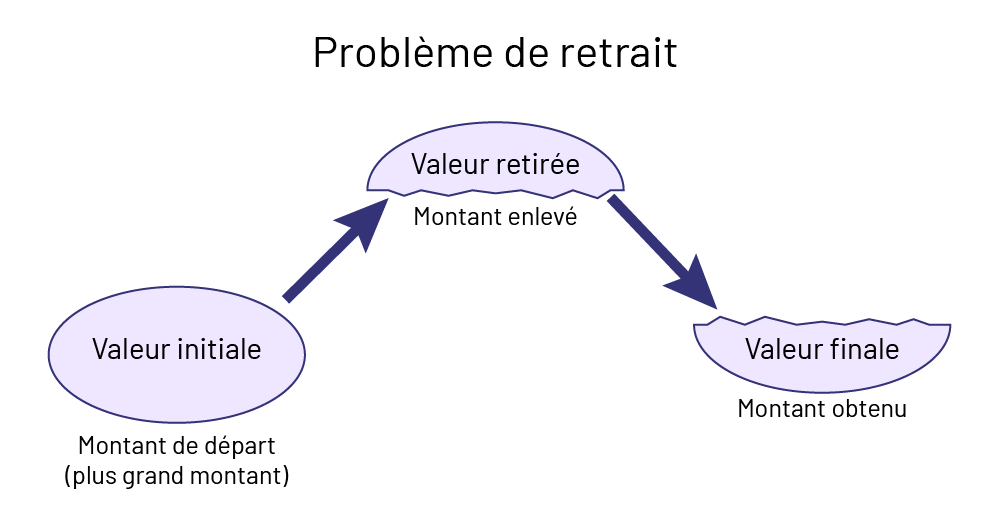Image Problème de retrait. Valeur initiale, montant de départ (parenthèse ouvrante) plus grand
montant (parenthèse fermante). Une flèche pointe
vers, valeur retirée, montant enlever. Une flèche pointe vers valeur finale, le montant obtenu.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 9.
Connaissance : problème de réunion
Les problèmes axés sur la relation partie-partie-tout comprennent 2 parties qui sont réunies en un tout.
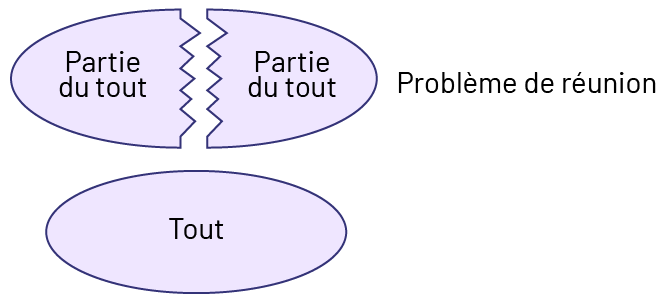Image Un ovale est divisé en deux. Dans une partie, on peut lire « partie du tout ». Dans l’autre
partie, on peut
lire « partie d’un tout ». C’est un problème de réunion. En dessous un ovale complet de la même taille que le
précédent où l’on peut lire « tout ».
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 9.
Connaissance : problème de comparaison
Dans les problèmes de comparaison, il s’agit de comparer 2 quantités. La 3e quantité représente la différence.
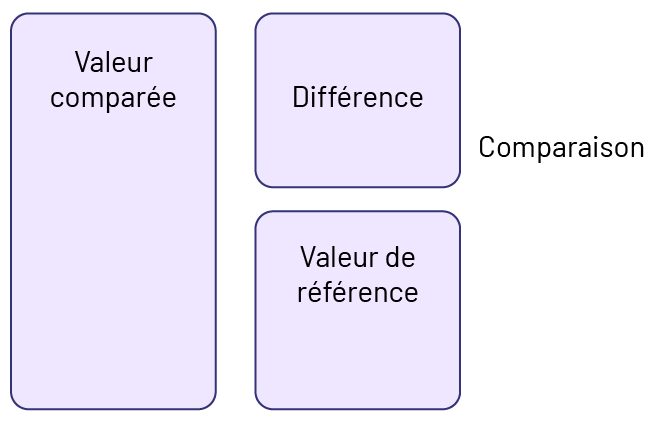Image Un grand rectangle où l’on peut lire : valeur comparée. 2 rectangles plus petits, placés
l’un en dessous de l’autre. Dans le premier on peut lire : différence, et dans le
deuxième : valeur de référence. À côté des rectangles, il y a le mot : comparaison.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 10.